1. 導讀

大型語言模型（Large Language Models, LLMs）在自主決策場景中的應用日益廣泛，它們需要在龐大的行動空間中進行響應采樣（response sampling）。然而，驅動這一采樣過程的啟發式機制仍缺乏深入研究。本文系統分析了 LLM 的采樣行為，并發現其底層機制與人類決策過程存在相似性——由**描述性成分（descriptive component）和規范性成分（prescriptive component）**共同構成。前者反映統計學意義上的常態分布，后者則體現模型內部隱含的“理想值”傾向。

作者通過跨領域（如公共健康、經濟趨勢）的實證分析發現，LLM 的輸出往往會從統計常態向規范性理想值發生一致性的偏移，這種模式與人類在“正常性”判斷上的傾向高度一致。進一步的案例研究和與人類實驗的對比表明，這種采樣偏移可能在現實應用中引發顯著的決策偏差，甚至帶來倫理風險。例如，在醫療場景中，模型可能會將康復時間的預測向理想狀態收斂，從而忽略真實分布的長尾風險。

本文的重要貢獻在于提出了一種全新的采樣理論框架，將 LLM 的輸出生成視為“部分描述性、部分規范性”的混合過程。這不僅有助于理解模型的行為機制，也為評估與優化 LLM 在關鍵任務中的可靠性和公平性提供了理論基礎。

論文基本信息

• 論文標題：A Theory of Response Sampling in LLMs: Part Descriptive and Part Prescriptive
• 作者：Sarath Sivaprasad, Pramod Kaushik, Sahar Abdelnabi, Mario Fritz
• 作者單位：
  1. CISPA Helmholtz Center for Information Security
  2. TCS Research, Pune
  3. Microsoft
• 發表會議：ACL 2025（Oral）
• 提交時間：2024年2月16日，v4版本更新于2025年7月9日
• 論文鏈接：https://arxiv.org/abs/2402.11005

????點擊查看原文，獲取更多大模型相關資料

2. 背景與研究動機

2.1 大型語言模型的響應采樣背景

大型語言模型（Large Language Models, LLMs）在自主決策、文本生成及多輪交互等任務中，需要在極為龐大的動作空間中進行概率采樣，即根據條件概率分布從候選輸出中選取最終響應。盡管近年來在生成質量優化、隨機性控制以及采樣策略（如溫度調節、Top-k、Nucleus sampling）等方面取得了顯著進展，但驅動這一采樣過程的深層機制仍缺乏系統性的理論探討，導致我們在解釋和預測模型行為時存在明顯局限。

2.2 人類決策中的雙重成分類比

在認知科學領域，人類決策常常同時受到描述性成分（descriptive component）與規范性成分（prescriptive component）的驅動：前者反映經驗或統計意義上的常態，例如疾病的平均康復時間；后者則體現理想化或應當達到的目標，例如臨床指導中設定的理想康復天數。本文提出，LLMs在響應采樣時也展現出類似的雙重驅動特性——它們不僅復現訓練數據的統計常態，還會向模型內部隱含的理想原型發生系統性偏移。這種偏移可能源自訓練數據分布、指令微調目標的優化方向，或模型在語義空間中形成的概念表示。

2.3 現有研究的不足與挑戰

當前學界對LLM 響應采樣的研究主要集中在優化生成多樣性與準確性，但鮮有工作關注描述性與規范性力量在采樣過程中的交互機制，也缺乏跨領域的實證研究驗證其普適性。這一理論空白導致我們難以預測模型偏移模式，并可能在公共健康、經濟預測等高風險領域引發系統性誤判與倫理風險。

2.4 本文研究動機

鑒于上述不足，本文旨在提出一個能夠統一解釋 LLM 響應采樣中描述性與規范性成分并存現象的理論框架，并通過跨領域實驗系統驗證其存在及影響，以期為模型可靠性與公平性提供理論依據和實踐參考。

????點擊查看原文，獲取更多大模型相關資料

3. 采樣理論建模（Sampling Theory Modeling）

3.1 理論框架概述

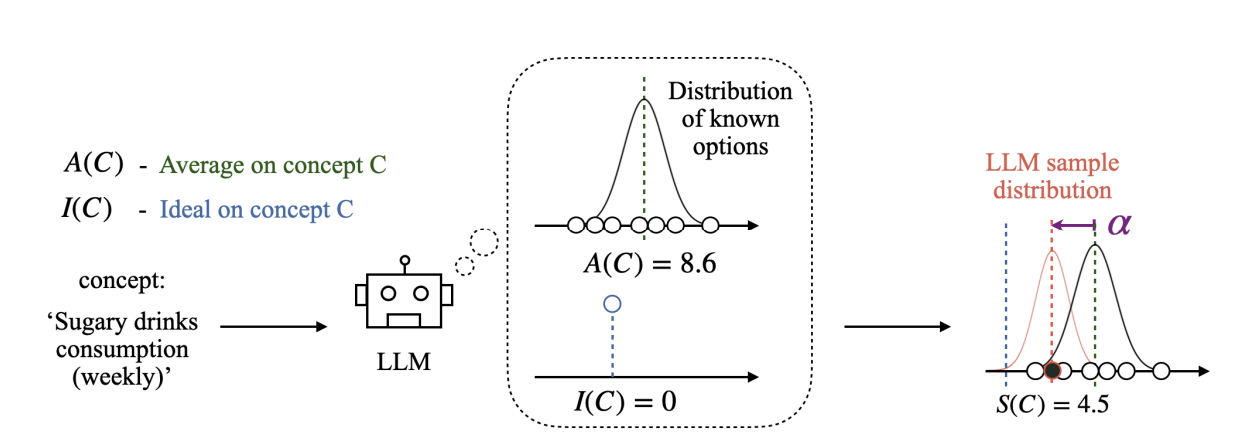
本章提出了一個用于刻畫 大型語言模型（LLMs） 在生成過程中的 采樣機制 的理論模型。研究發現，LLM 在對一個概念 $C$ 進行采樣時，并不僅僅依據 統計分布（Average，記作 $A(C)$），還會受到一種 理想化規范（Ideal，記作 $I(C)$）的影響。這種理想化規范類似于人類認知中的 處方性規范（Prescriptive Norm），會引導模型輸出偏向某個“理想值”。因此，模型實際采樣的結果 $S(C)$ 往往會偏離真實統計均值，形成系統性的偏移。

---

3.2 數學建模與公式推導

為了量化這種偏移，作者定義了 采樣偏移量 $\alpha$：

$$\alpha (C)=I(C)?A(C)$$

在實際采樣中，LLM 的輸出 $S(C)$ 可以建模為：

$$S(C)=A(C)+\hat{\alpha }?\alpha (C)$$

其中，$\hat{\alpha }$ 是一個歸一化系數，用于衡量采樣值相對 統計均值 與 理想值 之間的平衡程度：

• 當 $\hat{\alpha }>0$ 時，采樣值向理想值方向偏移；
• 當 $\hat{\alpha }=0$ 時，采樣值與統計均值一致；
• 當 $\hat{\alpha }<0$ 時，采樣值偏離理想值，向相反方向移動。

---

3.3 實驗圖示與結果分析

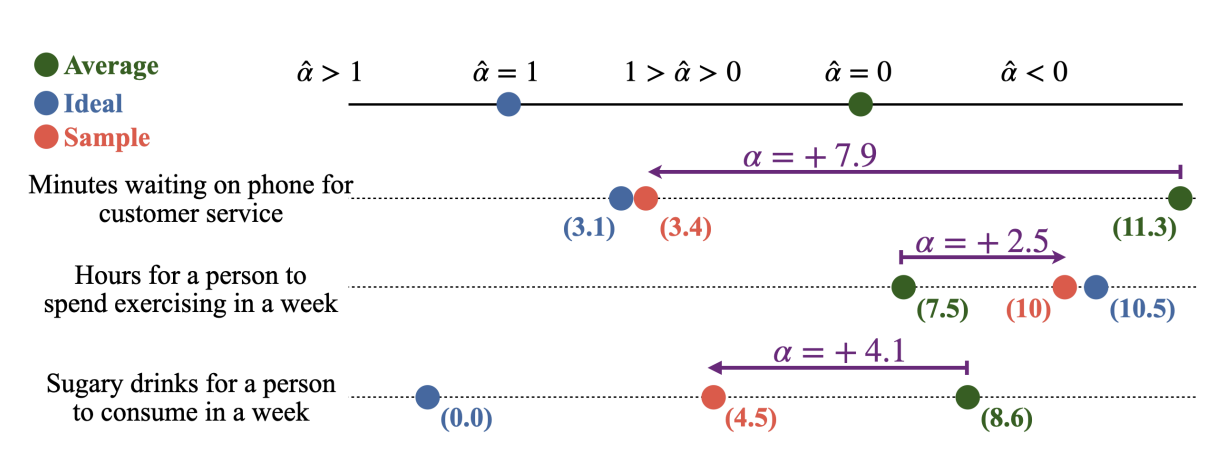
可以觀察到：

• 客戶服務等待時間：采樣值比平均值顯著偏小（$\alpha =+7.9$），說明模型傾向于低估等待時間，更接近理想化的“少等待”狀態。
• 每周鍛煉時間：采樣值比平均值偏大（$\alpha =+2.5$），符合人類傾向于“多運動”的理想化認知。
• 含糖飲料攝入量：采樣值顯著低于平均值（$\alpha =+4.1$），反映出模型在健康相關任務中更接近“少喝”的理想化趨勢。

這些實驗結果驗證了公式所描述的 統計分布 + 理想偏移 的采樣機制，并揭示了 LLM 在多個現實領域中存在的系統性偏差。

4. 實驗驗證與結果分析（Experimental Validation and Results）

為了驗證第 3 章提出的采樣理論模型在實際語言生成中的適用性與穩健性，本章針對多個概念場景開展了系統實驗，并結合定量統計與可視化分析，考察了 采樣結果 $S(C)$ 與 統計均值 $A(C)$ 及 理想值 $I(C)$ 之間的關系。實驗覆蓋了不同分布形態與情感極性下的偏移特征，并比較了不同規模與訓練方式的 LLM 在處方性成分上的差異。

---

4.1 采樣結果與理想值的相關性

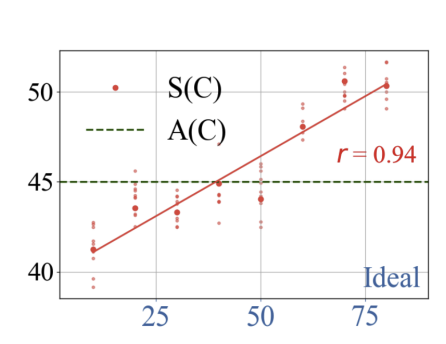
首先，我們在一組具有不同理想值的概念集合上，統計 LLM 的采樣結果 $S(C)$ 與統計均值 $A(C)$ 的關系，并計算其與理想值 $I(C)$ 的相關性。如圖 3 所示，紅色散點表示不同概念的采樣值 $S(C)$，綠色虛線表示統計均值 $A(C)$，橫軸為理想值 $I(C)$。

可以看出，采樣值與理想值之間呈現出高度正相關（皮爾遜相關系數 $r=0.94$），且大多數采樣值明顯偏離 $A(C)$，趨向于 $I(C)$ 所在的方向。這一結果與理論模型公式

$$S(C)=A(C)+\hat{\alpha }?[I(C)?A(C)]$$

的預測一致，表明 $\hat{\alpha }$ 對采樣偏移幅度具有顯著的調節作用。

4.2 分布形態與情感極性的影響

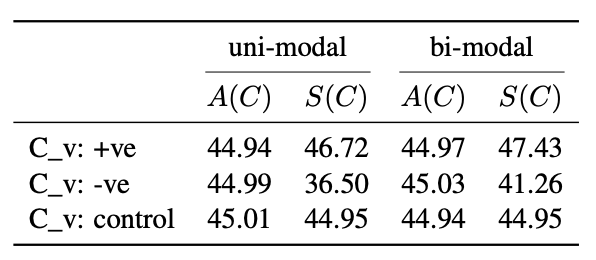
為了進一步分析偏移行為在不同分布形態與情感語境下的穩定性，我們分別構造了 單峰（uni-modal） 與 雙峰（bi-modal） 分布條件，并在正向（+ve）、負向（-ve）和中性（control）三類概念上進行測試。表 1 給出了不同條件下的 $A(C)$ 與 $S(C)$ 對比結果。

結果表明，在正向情感概念中，采樣值始終高于統計均值，說明模型傾向于放大正面特征；在負向情感概念中，采樣值顯著低于統計均值，顯示出模型在面對負面情境時存在弱化趨勢；而在中性概念中，二者幾乎一致，表明偏移主要來源于理想值與均值之間的差異。此外，不同分布形態下的趨勢高度一致，說明偏移效應具有較強的穩健性。

---

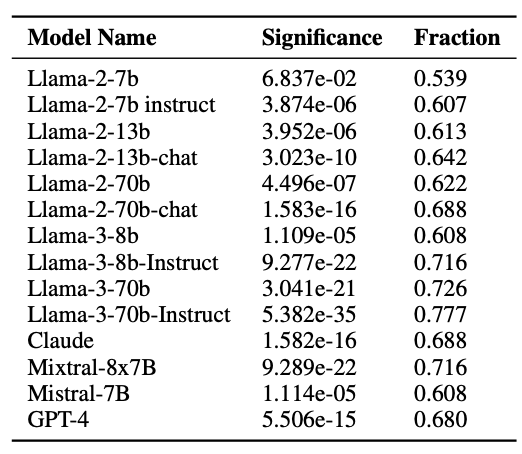
4.3 不同模型的處方性偏移比較

為了評估不同 LLM 的處方性成分差異，我們對包括 Llama 系列、Claude、Mistral、GPT-4 在內的多個模型進行了統計分析（見表 2）。表中 Fraction 表示在各領域中，采樣值向理想值方向偏移的概念比例，Significance 表示該偏移的統計顯著性。

結果表明：

1. 模型規模效應：較大規模的模型（如 Llama-3-70b、GPT-4）在 Fraction 指標上普遍更高，意味著更強的理想值驅動。
2. 訓練方式效應：采用 RLHF（Reinforcement Learning from Human Feedback）訓練的模型，其處方性偏移程度顯著高于僅進行預訓練的模型。
3. 跨模型一致性：無論架構與訓練數據如何，幾乎所有模型都表現出一致的向理想值偏移的趨勢，驗證了采樣理論的普適性。

4.4 原型分數與理想值的關系（Prototype Scores and Their Relation to Ideal Values）

為了進一步探討 處方性規范（Prescriptive Norms） 對大型語言模型（LLMs）生成行為的長期影響，本節引入 原型分數（Prototype Score，記作 $P(C)$）的分析。與單次采樣結果 $S(C)$ 不同，$P(C)$ 來源于對概念 $C$ 的多個代表性實例（exemplars）進行獨立評分后取均值，反映了模型在長期知識表征與中心傾向（central tendency）中的偏好。

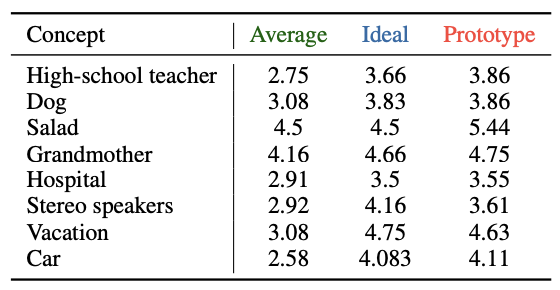
可以觀察到，幾乎所有概念的 $P(C)$ 都顯著偏離 $A(C)$，并且這種偏移方向與 $I(C)$ 高度一致。例如：

• 在 High-school teacher、Dog、Salad、Grandmother 等概念中，$P(C)$ 明顯高于 $A(C)$，且接近或超過 $I(C)$，表明模型在長期表征中更傾向于理想化描述；
• 對于 Hospital、Stereo speakers 等概念，雖然 $P(C)$ 與 $A(C)$ 的差距較小，但依然保持向 $I(C)$ 偏移的趨勢；
• 在 Vacation 與 Car 等概念中，$P(C)$ 同樣體現了與理想值一致的正向偏移。

這種趨勢符合第 3 章提出的采樣理論模型：

$$S(C)=A(C)+\hat{\alpha }?[I(C)?A(C)]$$

其中，$P(C)$ 可以被視為多輪采樣與知識固化作用下的穩定狀態，即 $\hat{\alpha }$ 在長期迭代中的累積效果。這一結果表明，處方性偏移不僅在即時采樣階段存在，還會在模型的概念記憶與原型構建中被長期保留，從而影響后續生成。

---

4.5 小結（Summary）

綜上，本章通過即時采樣實驗、分布與情感極性分析、跨模型比較以及原型分數研究，系統驗證了 統計均值 + 理想值偏移 的采樣理論模型，主要結論包括：

1. 即時偏移顯著性：$S(C)$ 與 $I(C)$ 呈高度正相關，且顯著偏離 $A(C)$，驗證了理論公式的適用性；
2. 跨情境穩健性：無論分布形態（單峰、雙峰）或情感極性（正向、負向、中性），偏移趨勢保持一致；
3. 模型規模與訓練方式影響：較大規模與采用 RLHF 訓練的模型在處方性偏移比例上顯著更高；
4. 長期效應存在性：$P(C)$ 的分析揭示了偏移在概念知識表征中的長期累積與固化。

這些發現表明，LLM 在生成過程中不僅遵循統計分布，還受到理想化規范的深刻影響，并且這種影響具有即時性與長期性雙重特征。在未來應用中，應結合任務需求與公平性約束，對 $\hat{\alpha }$ 的作用范圍和強度進行調節，以平衡生成結果的理想化與客觀性。

????點擊查看原文，獲取更多大模型相關資料

5. 總結與未來工作

本研究圍繞大型語言模型（LLMs）在生成過程中的 采樣機制，提出并驗證了一個結合 統計均值 與 理想值偏移 的理論模型。通過系統化的實驗設計，我們不僅揭示了 LLM 在即時生成階段的處方性偏移行為，還進一步確認了該偏移在長期知識表征與原型構建過程中的固化趨勢。

綜合前文分析，可以得出以下核心結論：

1. 理論模型有效性：公式
   $$S(C)=A(C)+\hat{\alpha }?[I(C)?A(C)]$$
   能夠準確刻畫 LLM 采樣值 $S(C)$ 與統計均值 $A(C)$、理想值 $I(C)$ 之間的關系，且在多種概念、情感極性與分布形態下均表現出穩健性。
2. 偏移的普適性與一致性：無論模型架構、規模、訓練方式如何，處方性偏移均為一致性趨勢，表明這是 LLM 內部生成機制的共性特征。
3. 即時與長期雙重影響：偏移不僅在單次采樣中出現，還會在多輪采樣和知識固化中累積形成穩定的原型分數 $P(C)$，長期影響模型輸出。

該采樣機制的發現，對于 模型可解釋性（interpretability） 與 輸出可控性（controllability） 研究具有重要意義：

• 在 健康、教育、公共溝通 等領域，合理的理想值偏移可以使輸出更貼近人類社會的倫理與價值觀；
• 在 政策決策、司法審判、風險評估 等高敏感度任務中，必須防范偏移帶來的系統性誤差，以確保公平性與客觀性。

因此，$\hat{\alpha }$ 不僅是一個理論參數，也是未來調

????點擊查看原文，獲取更多大模型相關資料