數據結構——查找（三、樹形查找）

一、二叉排序樹（BST）

1、二叉排序樹的定義

構造一棵二叉排序樹的目的并不是排序，而是提高查找、插入和刪除關鍵字的速度

二叉排序樹（也稱二叉搜索樹）或者是一顆空樹，或者是具有以下性質的二叉樹
1、若左子樹非空，則左子樹上所有結點的值均小于根節點的值
2、若右子樹非空，則右子樹上所有結點的值均大于根節點的值
3、左右子樹分別是一顆二叉排序樹
（右子樹所有結點的值均大于左子樹所有結點的值）

對二叉排序樹進行中序遍歷，可以得到一個遞增的有序序列

2、二叉排序樹的查找

二叉排序樹的查找是從根節點開始，是一個遞歸的過程

二叉排序樹的非遞歸查找算法，空間復雜度O(1)

//二叉排序樹的結點
typedef struct BSTNode{int key;struct BSTNode *lchild,*rchild;
}BSTNode, *BSTree;//二叉排序樹的非遞歸查找算法 
BSTNode *BST_Search(BSTree T, int key){while(T != NULL && key != T->key){ //若樹空或等于根節點值，則結束循環if(key < T->key){       //小于，則在左子樹上查找T = T->lchild;      //大于，則在右子樹上查找}else{T = T->rchild;}}return T;
}

二叉排序樹的遞歸查找算法，空間復雜度O(h)

//在二叉排序樹中查找值為key的結點（遞歸實現）
BSTNode *BST_Search_Recursion(BSTree T, int key){if(T == NULL){return NULL;    //查找失敗}if(key == T->key){return T;       //查找成功}else if(key < T->key){return BST_Search_Recursion(T->lchild, key);//在左子樹中找}else{return BST_Search_Recursion(T->rchild, key);//在右子樹中找}}

?3、二叉排序樹的插入

二叉排序樹是一顆動態樹，在查找過程中，當樹中不存在關鍵字值等于給定值的結點時進行插入。
若關鍵字的值小于根結點，則插入左子樹；反之，插入右子樹；
新插入的結點一定是一個葉節點，且是查找失敗時的查找路徑上訪問的最后一個結點的左孩子或右孩子
如圖，虛線表示查找路徑

在二叉排序樹中插入關鍵值為key的新結點（遞歸實現）

注：樹中存在相同關鍵字的結點會導致插入失敗

//在二叉排序樹中插入關鍵值為key的新結點（遞歸實現）
int BST_Insert(BSTree &T, int k){if(T == NULL){      //原樹為空，新插入的結點為根節點T = (BSTree)malloc(sizeof(BSTNode)); T->key = k;T->lchild = T->rchild = NULL;return 1;       //返回1，插入成功}else if(k == T->key){ //樹中存在相同關鍵字的結點，插入失敗return 0;}else if(k < T->key){   //插入到T的左子樹return BST_Insert(T->lchild, k);}else{                  //插入到T的右子樹return BST_Insert(T->rchild, k);}
}

在二叉排序樹中插入關鍵值為key的新結點（非遞歸實現）

//在二叉排序樹中插入關鍵值為key的新結點（非遞歸實現）
int BST_Insert2(BSTree &T, int key) {BSTNode *newNode = (BSTNode*)malloc(sizeof(BSTNode)); // 創建新節點newNode->key = key;newNode->lchild = newNode->rchild = NULL;if (T == NULL) {  // 如果樹為空，直接插入新節點作為根T = newNode;return 1; // 插入成功}BSTNode *parent = NULL;  // 用來記錄父節點BSTNode *current = T;    // 當前節點從根開始while (current != NULL) {parent = current;  // 記錄當前節點為父節點if (key == current->key) {free(newNode); // 如果樹中已有相同的key，插入失敗，釋放新節點return 0;  // 插入失敗}else if (key < current->key) {current = current->lchild;  // key 小于當前節點，移動到左子樹}else {current = current->rchild;  // key 大于當前節點，移動到右子樹}}// 在遍歷到NULL時，插入新節點if (key < parent->key) {parent->lchild = newNode;  // 插入到父節點的左子樹}else {parent->rchild = newNode;  // 插入到父節點的右子樹}return 1;  // 插入成功
}

4、二叉排序樹的構造

不同的輸入序列會得到不同的二叉排序樹
與二分查找判定樹不同，二分查找僅適用于有序的順序表，這也就意味著，同一個序列判定樹唯一。

//按照str[]中的關鍵字序列建立二叉排序樹
void create_BST(BSTree &T, int str[], int n){T = NULL;       //初始時T為空樹int i = 0;while(i < n){   //依次將每個關鍵字插入到二叉排序樹中BST_Insert(T, str[i]);i++;}
}

5、二叉排序樹的刪除

①若被刪除結點z是葉結點，則直接刪除，不會破壞二叉排序樹的性質;
②若結點z只有一棵左子樹或右子樹，則讓z的子樹替代z的位置；
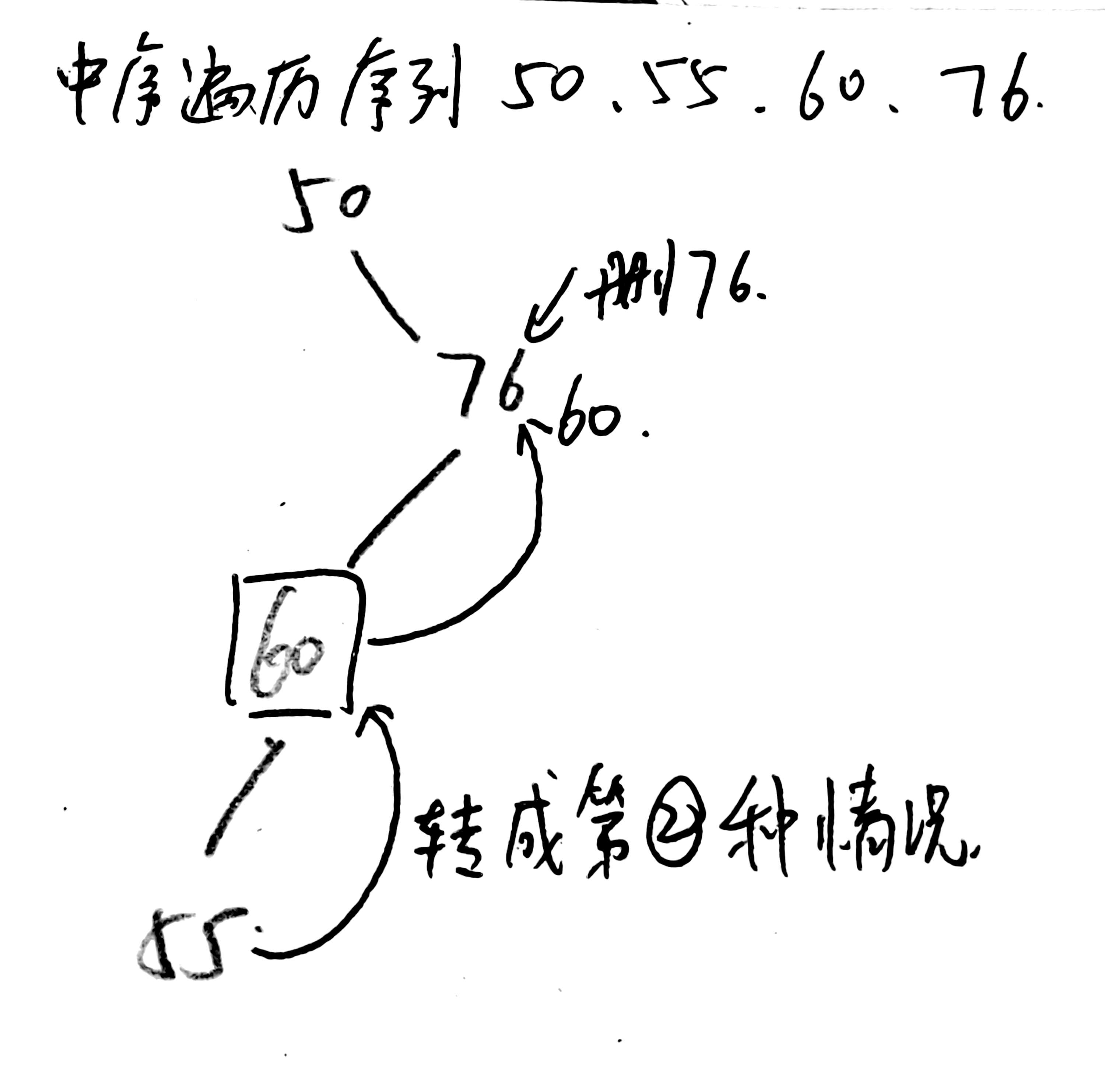
③若結點z有左、右兩棵子樹，則進行中序遍歷，讓z的直接后繼（或直接前驅）替代z，然后從二叉排序樹中刪去這個直接后繼（直接前驅），這樣就轉換成了第一或第二種的情況。

如圖，刪除76，為第③種情況，找到直接前驅，將直接前驅的值60替代76。而后轉變為刪除60，此時轉變成第②種情況，直接讓60的左子樹（55）替代60，并釋放55即可。

在二叉排序樹中刪除關鍵值為key的結點（遞歸實現）

// 查找二叉樹中的最小結點（即直接后繼）
BSTNode* findMin(BSTree T) {while (T && T->lchild) {T = T->lchild;}return T;
}// 查找二叉樹中的最大結點（即直接前驅）
BSTNode* findMax(BSTree T) {while (T && T->rchild) {T = T->rchild;}return T;
}// 在二叉排序樹中刪除關鍵值為key的結點（遞歸實現）
BSTree BST_Delete(BSTree T, int key) {if (T == NULL) {return T;  // 樹為空，直接返回}// 如果key小于當前結點的key，則在左子樹中刪除if (key < T->key) {T->lchild = BST_Delete(T->lchild, key);}// 如果key大于當前結點的key，則在右子樹中刪除else if (key > T->key) {T->rchild = BST_Delete(T->rchild, key);}// 找到要刪除的結點else {// 1. 刪除的是葉結點if (T->lchild == NULL && T->rchild == NULL) {free(T);  // 直接釋放該結點return NULL;  // 返回NULL，刪除該結點}// 2. 刪除的結點只有一個子樹else if (T->lchild == NULL) {  // 只有右子樹BSTNode* temp = T;T = T->rchild;  // 用右子樹替代free(temp);}else if (T->rchild == NULL) {  // 只有左子樹BSTNode* temp = T;T = T->lchild;  // 用左子樹替代free(temp);}// 3. 刪除的結點有兩個子樹else {// 找到當前結點的直接后繼（右子樹中的最小節點）BSTNode* temp = findMin(T->rchild);T->key = temp->key;  // 用后繼節點替代當前節點T->rchild = BST_Delete(T->rchild, temp->key);  // 刪除后繼結點}}return T;
}

6、二叉排序樹的查找效率分析

二叉排序樹的查找效率取決于樹的高度。
若二叉排序樹左右子樹的高度只差的絕對值不超過1（即平衡二叉樹），它的平均查找長度為O( $log_{2}n$ )成正比。
在最壞的情況下，若輸入序列為有序的，則會形成只有右孩子的單支樹，此時樹高為n，即平均查找長度為(n+1)/2

在查找方面，二叉排序樹和二分查找的性能差不多，但因為二叉排序樹與輸入序列有關，所以同一個序列兩種方法的平均查找長度（即效率）存在不同。
插入刪除結點維護有序性而言，二叉排序樹只需要移動指針，時間復雜度為O( $log_{2}n$ ）
而二分查找本身為有序順序表，插入或刪除需要移動大量元素，時間復雜度為O(n)

二、平衡二叉樹（AVL)

平衡因子=左子樹高-右子樹高
平衡二叉樹——平衡因子的絕對值不超過1

1、平衡二叉樹的插入

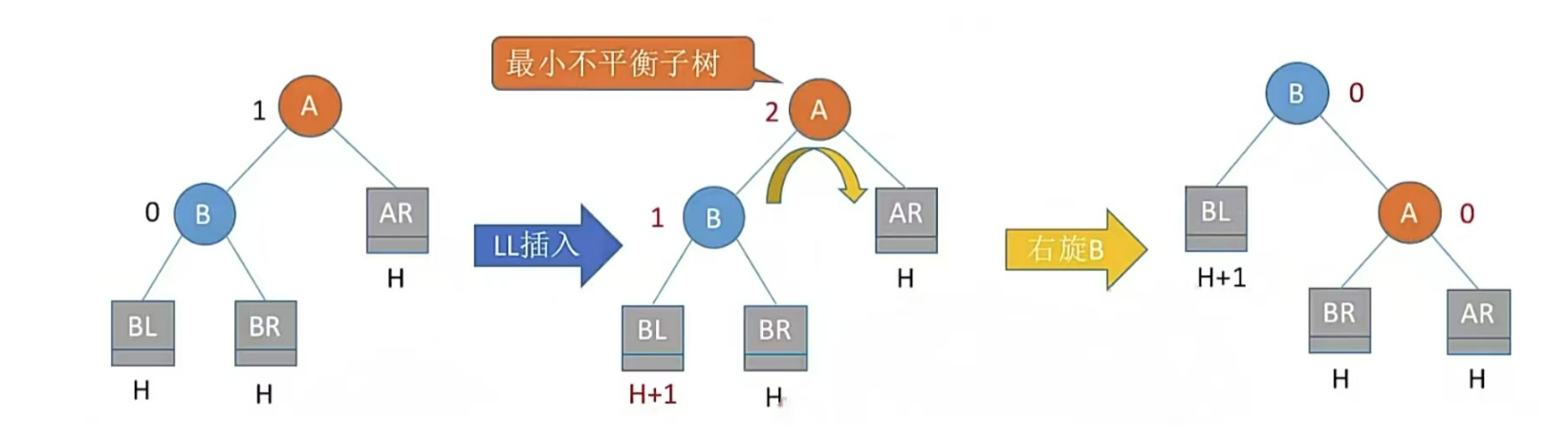
插入一個結點會造成4種情況，處理方法可使用口訣
只有左孩子右上旋，只有右孩子左上旋

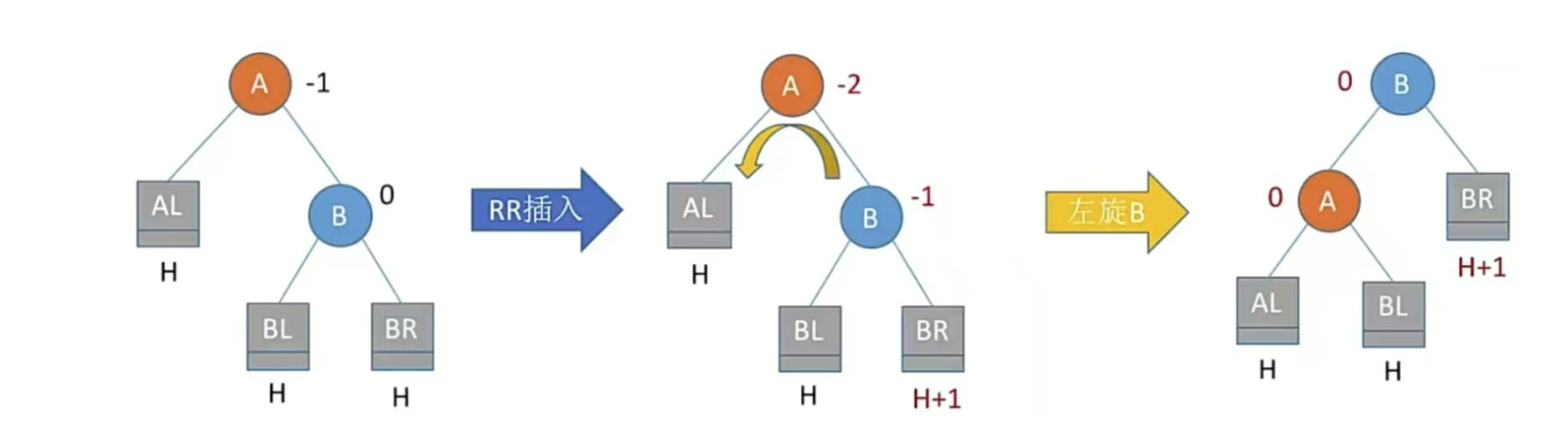
LL、RR兒子旋轉一次；LR、RL兒子、孫子各旋轉一次（共兩次）
RR型，右孩子的右子樹插入結點，即兒子右上旋轉
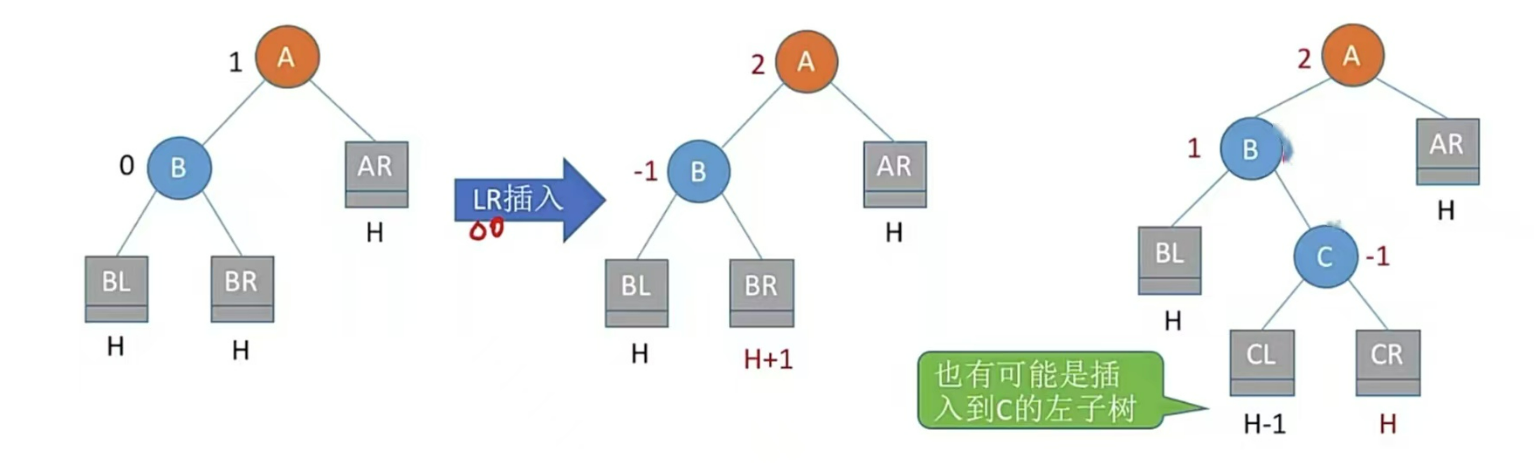
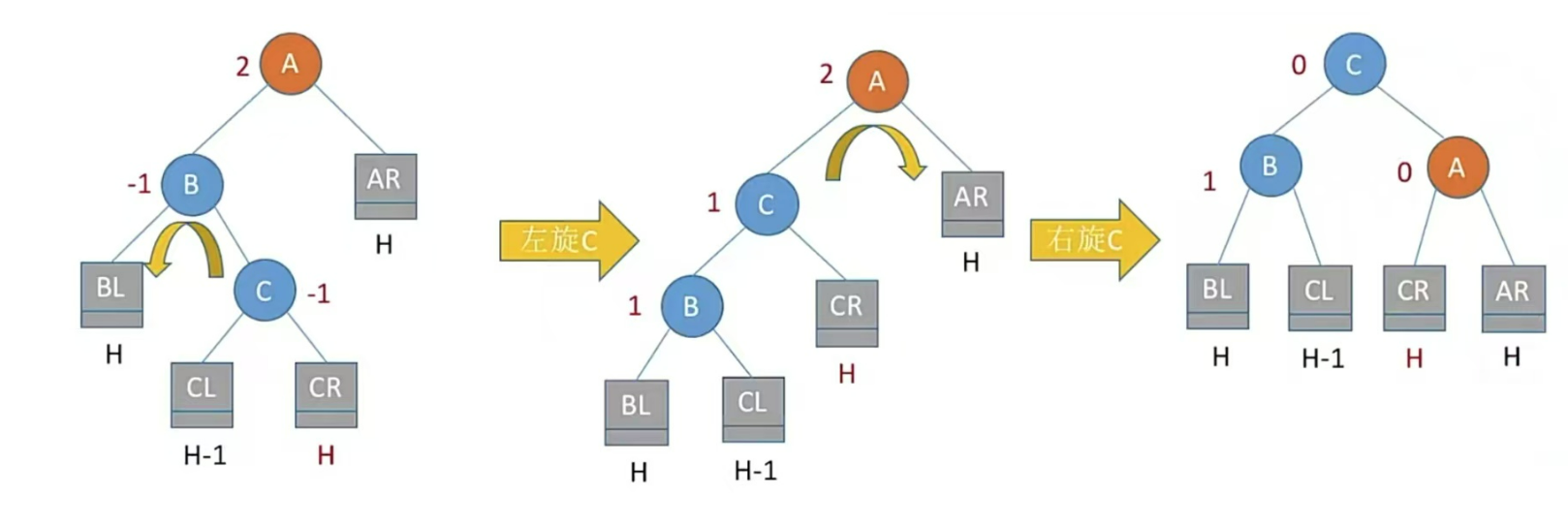
LR型，左孩子的右子樹插入結點，即孫子左上旋轉，兒子右上旋
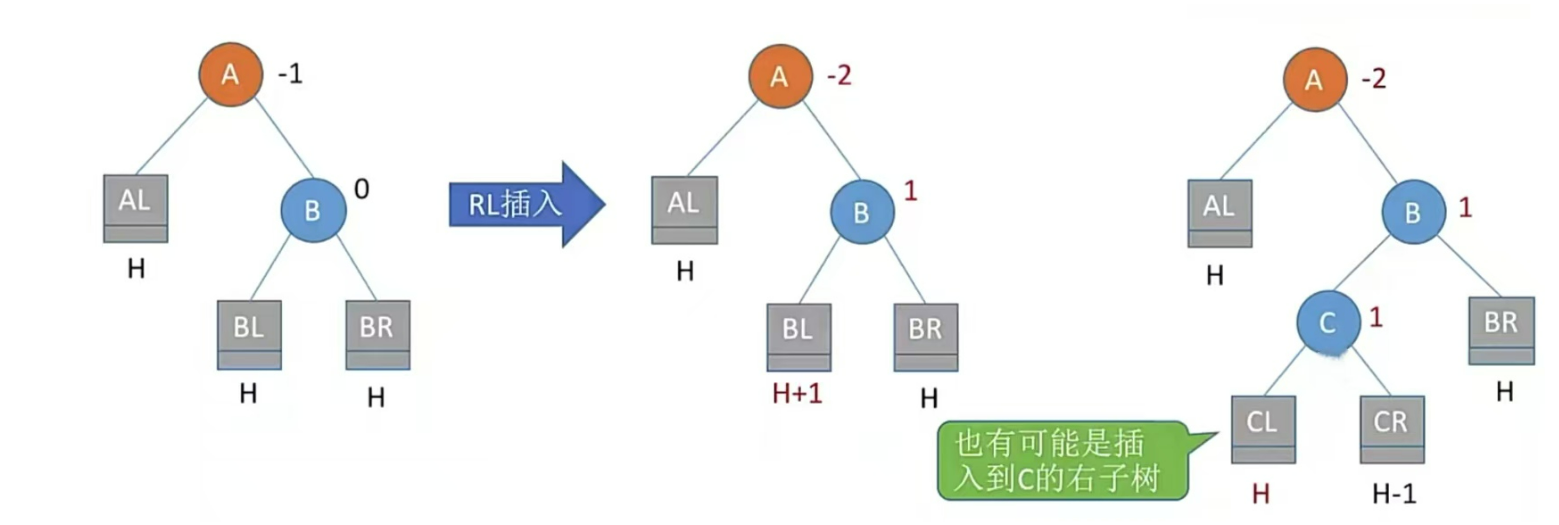
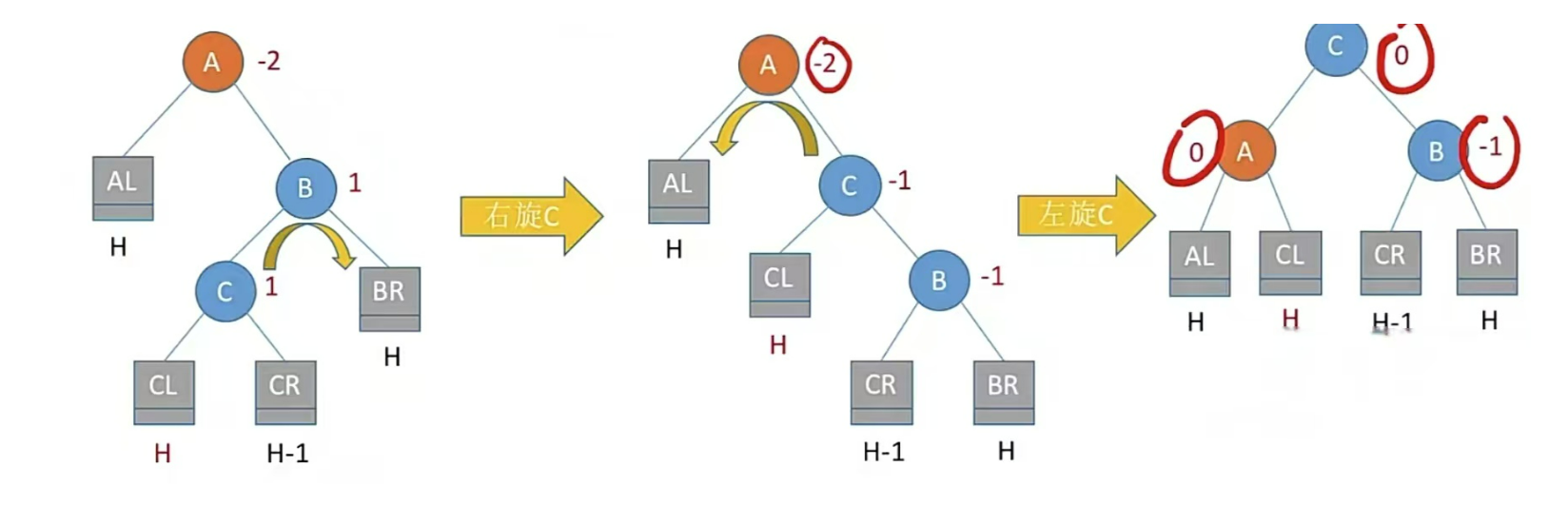
RL型，右孩子的左子樹插入結點，即孫子右上旋轉，兒子左上旋
注：LR和RL旋轉時，新結點究竟插入C的左子樹還是右子樹不影響旋轉結果。最終保證最底層沒有H+1

2、平衡二叉樹的刪除

刪除結點（方法同“二叉排序樹”）；
一路向北找到最小不平衡子樹，找不到就結束；
找最小不平衡子樹下，“個頭”最高的兒子、孫子；
根據孫子的位置，調整平衡（LL/RR/LR/RL）；
如果不平衡向上傳導，回到第2條。

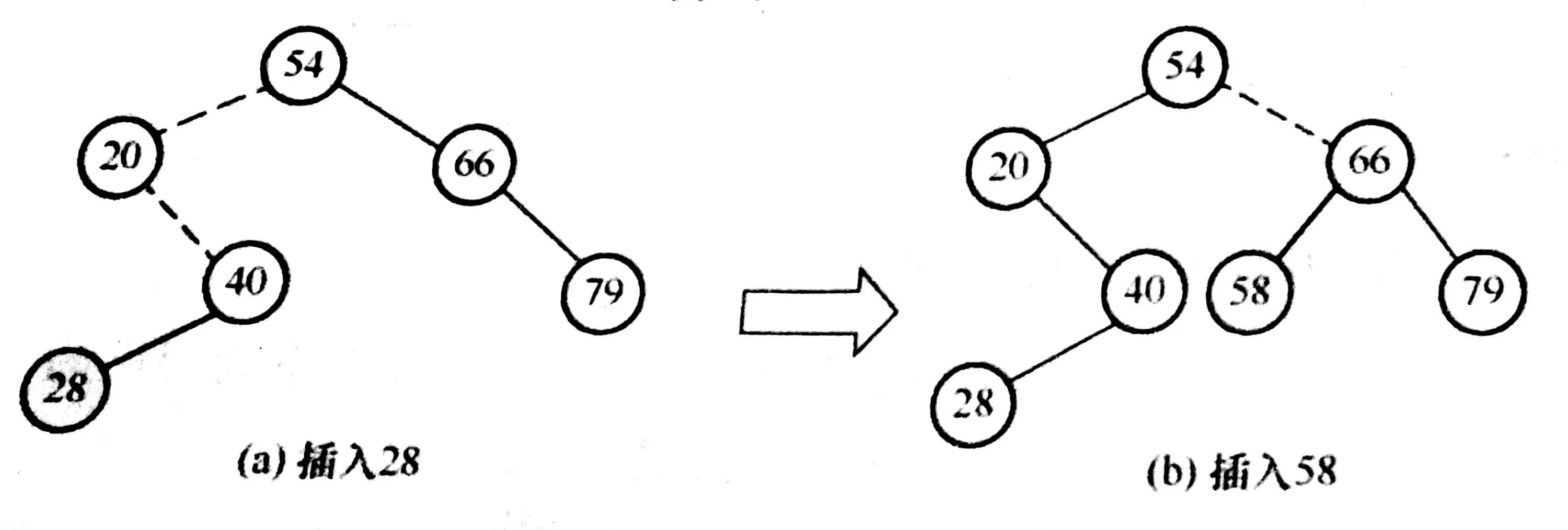
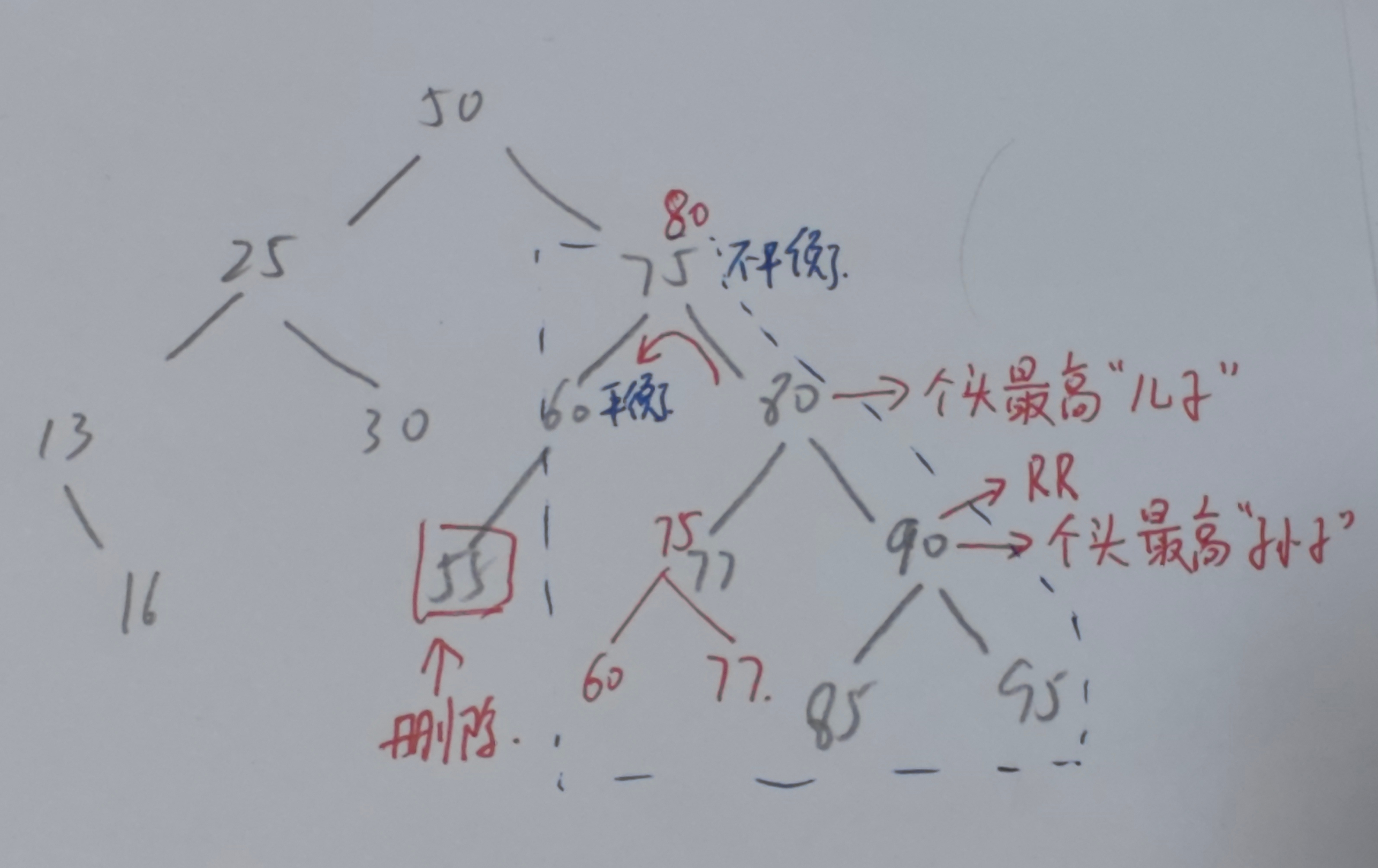
如圖，紅筆所示為刪除后的替換
若要刪除55，此時55為葉子結點，直接刪除
刪除之后一路向北，60仍然平衡，左右子樹均為空；75不平衡，左子樹高為1，右子樹高為3
找個頭最高的兒子為80，個頭最高的孫子為90
孫子90位于爺爺80的RR型，只需要兒子進行左上旋
調整完畢，向北探查，發現50也平衡，調整結束

3、平衡二叉樹的查找效率

假設以 $n_{h}$ 表示深度為h的平衡樹中含有的最少結點數，則：
有 $n_{0}$ = 0， $n_{1}$ = 1， $n_{2}$ = 2，并且有 $n_{h}$ ?= $n_{h-1}$ ?+ $n_{h-2}$ ?+ 1
含有n個結點的平衡二叉樹的最大深度有遞推式推出，即O( $log_{2}n$ ）
最小深度即滿二叉樹情況

三、紅黑樹

平衡二叉樹（AVL）：在執行插入或刪除操作時，容易破壞其平衡性，因此需要頻繁調整樹拓撲結構。例如，當插入操作導致不平衡時，系統需要先計算平衡因子，定位最小不平衡子樹（這一過程耗時較大），然后執行LL/RR/LR/RL等旋轉操作來恢復平衡。
紅黑樹（RBT）：在插入或刪除操作時，通常能夠保持其紅黑特性，因此不需要頻繁調整樹結構。即使需要調整，也往往能在常數時間內完成操作。
在實際使用中，平衡二叉樹適用于以查為主，很少插入/刪除的應用場景；而紅黑樹適用于頻繁插入/刪除的場景，實用性更強。

1、紅黑樹的定義

紅黑樹本質上是二叉排序樹
但是在插入時可以插入重復值

滿足如下性質的二叉排序樹即為紅黑樹：
滿足左子樹結點值 ≤ 根節點值 ≤ 右子樹結點值；
每個結點或是紅色的，或是黑色的；
根節點是黑色的；
葉結點（外部結點、NULL結點、失敗結點）均是黑色的；
不存在兩個相鄰的紅結點（即紅結點的父節點和孩子結點均是黑色）；
對每個結點，從該節點到任一葉結點的簡單路徑上，所含黑結點的數目相同。
左根右，根葉黑，不紅紅，黑路同

紅黑樹的結點定義

struct RBNode{          //紅黑樹的結點定義int key;            //關鍵字的值RBNode* parent;     //雙親結點指針RBNode* lchild;     //左孩子指針RBNode* rchild;     //右孩子指針int color;          //結點顏色，如：可用0/1表示黑/紅，也可以使用枚舉型enum表示顏色
};

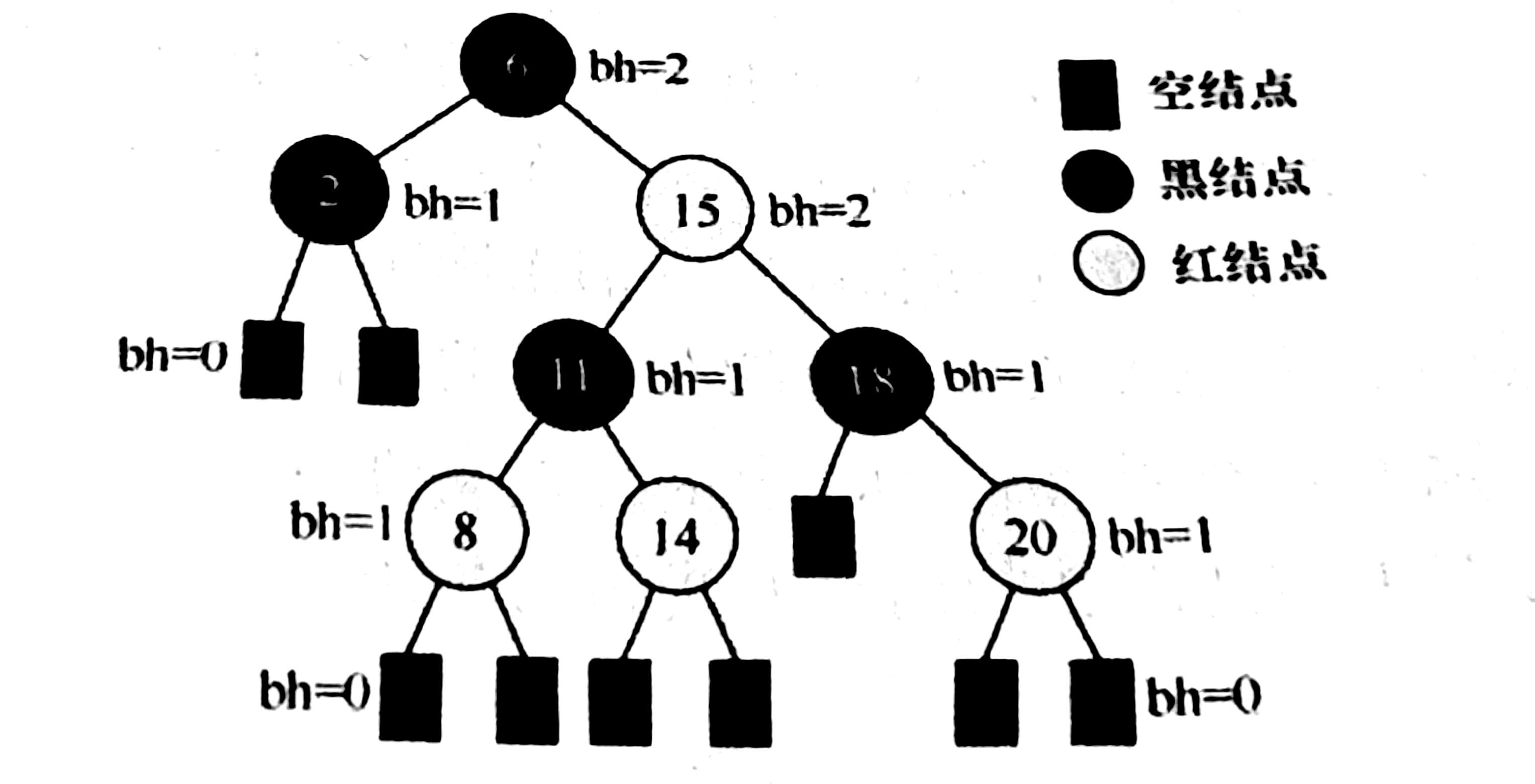
1、從某個結點（不包含該結點）出發，到達一個葉結點的任意一個簡單路徑上的黑結點總數稱為該結點的黑高。（由性質6黑路同確定）
2、從根結點到葉結點的最長路徑不大于最短路徑的兩倍。
3、根結點黑高為h，至少 $2^{h}-1$ 內部結點，即只有黑結點，并且滿樹的情況。（由性質56確定），最多是 $2^{2h}-1$
4、由于紅結點最多間隔插入黑結點，所以黑高 $h\geq \frac{h}{2}$ ，于是 $n\geq 2^{h/2}+1$

2、紅黑樹的插入

1、先查找，確定插入位置（原理同二叉排序樹），插入新結點
2、新結點是根——染為黑色
3、新結點非根——染為紅色
若插入新結點后依然滿足紅黑樹定義，則插入結束
若插入新結點后不滿足紅黑樹定義，需要調整，使其重新滿足紅黑樹定義
? ? ? ? ? ? ? ? ? 黑叔：旋轉+染色
? ? ? ? ? ? ? ? ? ? ? ? ? LL型：右單旋，父換爺+染色
? ? ? ? ? ? ? ? ? ? ? ? ? RR型：左單旋，父換爺+染色
? ? ? ? ? ? ? ? ? ? ? ? ? LR型：左、右雙旋，兒換爺+染色
? ? ? ? ? ? ? ? ? ? ? ? ? RL型：右、左雙旋，兒換爺+染色
? ? ? ? ? ? ? ? ? 紅叔：染色+變新
? ? ? ? ? ? ? ? ? ? ? ? ? 叔父爺染色，爺變為新結點

紅黑樹的插入，更多注意不紅紅的情況，而后是根葉黑，至于左根右、黑路同，在插入的時候規則就考慮了。

四、完整代碼實現

1、二叉排序樹部分

#include <iostream>
#include <cstdlib>using namespace std;//二叉排序樹的結點
typedef struct BSTNode{int key;struct BSTNode *lchild,*rchild;
}BSTNode, *BSTree;//二叉排序樹的非遞歸查找算法 
BSTNode *BST_Search(BSTree T, int key){while(T != NULL && key != T->key){ //若樹空或等于根節點值，則結束循環if(key < T->key){       //小于，則在左子樹上查找T = T->lchild;      //大于，則在右子樹上查找}else{T = T->rchild;}}return T;}//在二叉排序樹中查找值為key的結點（遞歸實現）
BSTNode *BST_Search_Recursion(BSTree T, int key){if(T == NULL){return NULL;    //查找失敗}if(key == T->key){return T;       //查找成功}else if(key < T->key){return BST_Search_Recursion(T->lchild, key);//在左子樹中找}else{return BST_Search_Recursion(T->rchild, key);//在右子樹中找}}//在二叉排序樹中插入關鍵值為key的新結點（遞歸實現）
int BST_Insert(BSTree &T, int k){if(T == NULL){      //原樹為空，新插入的結點為根節點T = (BSTree)malloc(sizeof(BSTNode)); T->key = k;T->lchild = T->rchild = NULL;return 1;       //返回1，插入成功}else if(k == T->key){ //樹中存在相同關鍵字的結點，插入失敗return 0;}else if(k < T->key){   //插入到T的左子樹return BST_Insert(T->lchild, k);}else{                  //插入到T的右子樹return BST_Insert(T->rchild, k);}
}//在二叉排序樹中插入關鍵值為key的新結點（非遞歸實現）
int BST_Insert2(BSTree &T, int key) {BSTNode *newNode = (BSTNode*)malloc(sizeof(BSTNode)); // 創建新節點newNode->key = key;newNode->lchild = newNode->rchild = NULL;if (T == NULL) {  // 如果樹為空，直接插入新節點作為根T = newNode;return 1; // 插入成功}BSTNode *parent = NULL;  // 用來記錄父節點BSTNode *current = T;    // 當前節點從根開始while (current != NULL) {parent = current;  // 記錄當前節點為父節點if (key == current->key) {free(newNode); // 如果樹中已有相同的key，插入失敗，釋放新節點return 0;  // 插入失敗}else if (key < current->key) {current = current->lchild;  // key 小于當前節點，移動到左子樹}else {current = current->rchild;  // key 大于當前節點，移動到右子樹}}// 在遍歷到NULL時，插入新節點if (key < parent->key) {parent->lchild = newNode;  // 插入到父節點的左子樹}else {parent->rchild = newNode;  // 插入到父節點的右子樹}return 1;  // 插入成功
}//按照str[]中的關鍵字序列建立二叉排序樹
void create_BST(BSTree &T, int str[], int n){T = NULL;       //初始時T為空樹int i = 0;while(i < n){   //依次將每個關鍵字插入到二叉排序樹中BST_Insert(T, str[i]);i++;}
}// 查找二叉樹中的最小結點（即直接后繼）
BSTNode* findMin(BSTree T) {while (T && T->lchild) {T = T->lchild;}return T;
}// 查找二叉樹中的最大結點（即直接前驅）
BSTNode* findMax(BSTree T) {while (T && T->rchild) {T = T->rchild;}return T;
}// 在二叉排序樹中刪除關鍵值為key的結點（遞歸實現）
BSTree BST_Delete(BSTree T, int key) {if (T == NULL) {return T;  // 樹為空，直接返回}// 如果key小于當前結點的key，則在左子樹中刪除if (key < T->key) {T->lchild = BST_Delete(T->lchild, key);}// 如果key大于當前結點的key，則在右子樹中刪除else if (key > T->key) {T->rchild = BST_Delete(T->rchild, key);}// 找到要刪除的結點else {// 1. 刪除的是葉結點if (T->lchild == NULL && T->rchild == NULL) {free(T);  // 直接釋放該結點return NULL;  // 返回NULL，刪除該結點}// 2. 刪除的結點只有一個子樹else if (T->lchild == NULL) {  // 只有右子樹BSTNode* temp = T;T = T->rchild;  // 用右子樹替代free(temp);}else if (T->rchild == NULL) {  // 只有左子樹BSTNode* temp = T;T = T->lchild;  // 用左子樹替代free(temp);}// 3. 刪除的結點有兩個子樹else {// 找到當前結點的直接后繼（右子樹中的最小節點）BSTNode* temp = findMin(T->rchild);T->key = temp->key;  // 用后繼節點替代當前節點T->rchild = BST_Delete(T->rchild, temp->key);  // 刪除后繼結點}}return T;
}// 在二叉排序樹中刪除關鍵值為key的結點（非遞歸實現）
BSTree BST_Delete2(BSTree T, int key) {BSTNode* parent = NULL;BSTNode* current = T;while (current != NULL && current->key != key) {parent = current;if (key < current->key) {current = current->lchild;} else {current = current->rchild;}}// 如果樹中沒有該結點if (current == NULL) {return T;  // 不刪除任何結點}// 刪除的結點有兩個子樹if (current->lchild != NULL && current->rchild != NULL) {// 找到右子樹中的最小結點作為后繼BSTNode* successorParent = current;BSTNode* successor = current->rchild;while (successor->lchild != NULL) {successorParent = successor;successor = successor->lchild;}// 替換當前結點的值為后繼結點的值current->key = successor->key;// 刪除后繼結點if (successorParent->lchild == successor) {successorParent->lchild = successor->rchild;} else {successorParent->rchild = successor->rchild;}free(successor);}// 刪除的結點沒有左子樹，只有右子樹else if (current->lchild == NULL) {if (parent == NULL) { // 如果刪除的是根結點T = current->rchild;} else if (parent->lchild == current) {parent->lchild = current->rchild;} else {parent->rchild = current->rchild;}free(current);}// 刪除的結點沒有右子樹，只有左子樹else if (current->rchild == NULL) {if (parent == NULL) { // 如果刪除的是根結點T = current->lchild;} else if (parent->lchild == current) {parent->lchild = current->lchild;} else {parent->rchild = current->lchild;}free(current);}return T;
}void inorderTraversal(BSTree T) {if (T != NULL) {inorderTraversal(T->lchild);cout << T->key << " ";inorderTraversal(T->rchild);}
}int main() {BSTree T = NULL;int keys[] = {50, 30, 70, 20, 40, 60, 80};int n = sizeof(keys) / sizeof(keys[0]);// 創建二叉排序樹create_BST(T, keys, n);// 打印樹的中序遍歷cout << "中序遍歷輸出：";inorderTraversal(T);cout << endl;// 查找某個元素int searchKey = 40;BSTNode* result = BST_Search(T, searchKey);if (result != NULL) {cout << "找到節點：" << result->key << endl;} else {cout << "未找到節點" << endl;}// 遞歸查找result = BST_Search_Recursion(T, searchKey);if (result != NULL) {cout << "遞歸查找找到節點：" << result->key << endl;} else {cout << "遞歸查找未找到節點" << endl;}// 刪除一個結點并展示中序遍歷int deleteKey = 70;cout << "刪除結點 " << deleteKey << endl;T = BST_Delete(T, deleteKey);inorderTraversal(T);cout << endl;return 0;
}