題目

邏輯表達式是計算機科學中的重要概念和工具，包含邏輯值、邏輯運算、邏輯運算優先級等內容。
在一個邏輯表達式中，元素的值只有兩種可能：0（表示假）和 1（表示真）。元素之間有多種可能的邏輯運算，本題中只需考慮如下兩種：“與”（符號為 &）和“或”（符號為 |）。其運算規則如下：
0&0=0&1=1&0=0，1&1=1；
0∣0=0，0∣1=1∣0=1∣1=1。
在一個邏輯表達式中還可能有括號。規定在運算時，括號內的部分先運算；兩種運算并列時，& 運算優先于 | 運算；同種運算并列時，從左向右運算。
比如，表達式 0|1&0 的運算順序等同于 0|(1&0)；表達式 0&1&0|1 的運算順序等同于 ((0&1)&0)|1。
此外，在 C++ 等語言的有些編譯器中，對邏輯表達式的計算會采用一種“短路”的策略：在形如 a&b 的邏輯表達式中，會先計算 a 部分的值，如果 a=0，那么整個邏輯表達式的值就一定為 0，故無需再計算 b 部分的值；同理，在形如 a|b 的邏輯表達式中，會先計算 a 部分的值，如果 a=1，那么整個邏輯表達式的值就一定為 1，無需再計算 b 部分的值。
現在給你一個邏輯表達式，你需要計算出它的值，并且統計出在計算過程中，兩種類型的“短路”各出現了多少次。需要注意的是，如果某處“短路”包含在更外層被“短路”的部分內則不被統計，如表達式 1|(0&1) 中，盡管 0&1 是一處“短路”，但由于外層的 1|(0&1) 本身就是一處“短路”，無需再計算 0&1 部分的值，因此不應當把這里的 0&1 計入一處“短路”。

輸入格式
輸入共一行，一個非空字符串 s 表示待計算的邏輯表達式。

輸出格式
輸出共兩行，第一行輸出一個字符 0 或 1，表示這個邏輯表達式的值；第二行輸出兩個非負整數，分別表示計算上述邏輯表達式的過程中，形如 a&b 和 a|b 的“短路”各出現了多少次。

輸入輸出樣例
輸入 #1
0&(1|0)|(1|1|1&0)
輸出 #1
1
1 2
輸入 #2
(0|1&0|1|1|(1|1))&(0&1&(1|0)|0|1|0)&0
輸出 #2
0
2 3
說明/提示
【樣例解釋 #1】
該邏輯表達式的計算過程如下，每一行的注釋表示上一行計算的過程：

0&(1|0)|(1|1|1&0)
=(0&(1|0))|((1|1)|(1&0)) //用括號標明計算順序
=0|((1|1)|(1&0)) //先計算最左側的 &，是一次形如 a&b 的“短路”
=0|(1|(1&0)) //再計算中間的 |，是一次形如 a|b 的“短路”
=0|1 //再計算中間的 |，是一次形如 a|b 的“短路”
=1
【數據范圍】

設 ∣s∣ 為字符串 s 的長度。

對于所有數據，1≤∣s∣≤10
6
。保證 s 中僅含有字符 0、1、&、|、(、) 且是一個符合規范的邏輯表達式。保證輸入字符串的開頭、中間和結尾均無額外的空格。保證 s 中沒有重復的括號嵌套（即沒有形如 ((a)) 形式的子串，其中 a 是符合規范的邏輯表達式）。

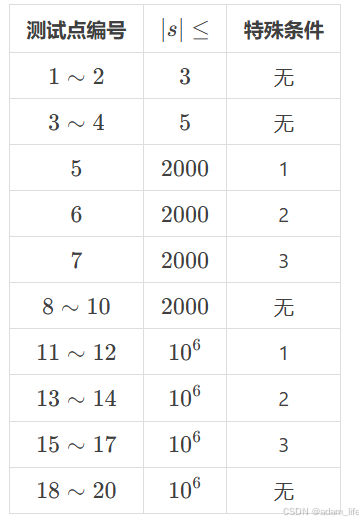
其中：
特殊性質 1 為：保證 s 中沒有字符 &。
特殊性質 2 為：保證 s 中沒有字符 |。
特殊性質 3 為：保證 s 中沒有字符 ( 和 )。

【提示】

以下給出一個“符合規范的邏輯表達式”的形式化定義：

字符串 0 和 1 是符合規范的；
如果字符串 s 是符合規范的，且 s 不是形如 (t) 的字符串（其中 t 是符合規范的），那么字符串 (s) 也是符合規范的；
如果字符串 a 和 b 均是符合規范的，那么字符串 a&b、a|b 均是符合規范的；
所有符合規范的邏輯表達式均可由以上方法生成。

代碼

#include <bits/stdc++.h>//萬能頭文件，包含c++標準庫中常用頭文件 
using namespace std;//使用std命名空間，使用標準庫中類型、函數時無需std::前綴 
int n_yu,n_huo; //與和或運算短路次數 
struct node{//二叉樹節點類型 char x;//操作符號'&'、'|'、'('、')' 、'0'、'1' bool k;//各邏輯運算結果 node *fa, *left, *right;//指向父、左、右節點的指針 node() : x('*'),fa(nullptr), left(nullptr), right(nullptr) {}//默認構造函數，初始化節點 node(char cx){//帶參構造函數，根據字符初始化節點 x=cx,fa=nullptr, left=nullptr, right=nullptr;if(cx=='1'||cx=='0')k=cx-'0';}
};
class Tree{public:node *root,*current;    // 根節點指針,當前操作節點指針(構建樹時用)// 構造函數：初始化根節點和當前節點Tree(){//構造函數，構造根節點為'r'（不變）,當前節點指向根 root=new node('r'), current=root;}~Tree() {// 析構函數：遞歸釋放整個語法樹節點內存clear(root);root = current = nullptr;}void insert(char x) {//根據字符類型，插入并構建語法樹     node* newNode = new node(x);// 創建新節點if(x=='0'||x=='1'||x=='('){//操作數和左括號 newNode->fa = current;//成為當前節點的子節點 if(!current->left)current->left = newNode;//當前節點左子節點空，就掛到左節點 else if(!current->right)current->right = newNode;//否則掛右節點 }else if(x==')'){//右括號時要歸攏，調整當前位置回到左括號處 current=current->fa;//下句無法越過當前的左括號，添加該句主動升一層 while(current->x!='(')current=current->fa;//循環一直找到左括號位置 newNode->fa=current;current->right=newNode;//左括號節點的右節點是右括號 newNode=newNode->fa;//左括號調整為當前節點位置 }else if(x=='|'){//優先級在|和&下，當前位置升到緊鄰左括號或者根前 while(current->fa->x!='('&&current->fa!=root)current=current->fa;current->fa->left=newNode;newNode->fa=current->fa;//|變成當前節點父節點的左子， current->fa=newNode;newNode->left=current;//當前節點變成|的左子 }else if(x=='&'){//如果父節點是|，則&優先級高，要下潛。否則遇到&就得上浮 if(current->fa->x=='|'){current->fa->right=newNode;newNode->fa=current->fa;//當前節點的父節點變成&的父節點， current->fa=newNode;newNode->left=current;//當前節點變成&節點的左節點 }else{while(current->fa->x=='&')current=current->fa;//父是&就得上浮，得父不是&得節點為當前節點 if(current->fa->left==current)current->fa->left=newNode;//當前節點是父節點的左子，掛父節點的左樹 else current->fa->right=newNode;//掛父節點的右樹 newNode->fa=current->fa;current->fa=newNode;newNode->left=current;//當前節點(&)掛插入節點的左樹 }}current=newNode;//插入的節點變成當前節點(括號選左括號) }void clear(node* x) {// 遞歸清除節點及其子節點if (!x) return;clear(x->left);clear(x->right);delete x;}void view1(node *x){cout<<x->x;if(x->left)view1(x->left);if(x->right)view1(x->right);}void view3(node *x){if(x->left)view3(x->left);cout<<x->x;if(x->right)view3(x->right);}void view2(node *x){cout<<x->x<<"["<<x->k<<"] ";if(x->left)view2(x->left);if(x->right)view2(x->right);}bool run(node *n){bool k1,k2; //左右樹運算結果 if(n->x=='r')return n->k=run(n->left);//根和左括號處結果僅源自左樹 if(n->x=='(')return n->k=run(n->left);//右括號不影響結果 if(n->x=='0'||n->x=='1')return n->k;//運算數 if(n->x=='&'){//與運算 k1=run(n->left);//先算左樹 if(k1==0){//如果左樹是0，直接返回0，不用算右樹 n_yu++;return n->k=0;}k2=run(n->right);return n->k=k1&&k2;}if(n->x=='|'){//或運算 k1=run(n->left);if(k1==1){//如果左樹是1，直接返回1，不用算右樹 n_huo++;return n->k=1;}k2=run(n->right);return n->k=k1||k2;}}
}tree;
int main(){//freopen("expr.in","r",stdin);string s;cin>>s;for(int i=0;s[i];i++){tree.insert(s[i]); //cout<<i<<" "<<s[i]<<"先序";tree.view1(tree.root);cout<<endl;}//cout<<"先序";tree.view1(tree.root);cout<<endl;//cout<<"中序";tree.view3(tree.root);cout<<endl;cout<<tree.run(tree.root)<<endl;cout<<n_yu<<" "<<n_huo<<endl;//cout<<"先序";tree.view2(tree.root);cout<<endl;return 0;
}

思路

1.構建二叉樹，n個字符n次操作，)、|和&需要上溯，最差情況是從當前節點回溯到根節點(n次),所以時間復雜度是o(n^2),這里n=10 ^6，結果是10 ^12，大于1秒的大約次數10 ^8次。有可能會超時——還好沒有。
遍歷邏輯表達式，每個字符建立一個指針空間節點
將所有節點連接成二叉樹
經過一些樣例數據的實操，得到邏輯關系
root
開始就有，用r標記，位置不變。后繼只有左沒有右
0、1、(
添(節點，或左或右
)
上溯，找到(節點,成為(節點的右節點，父(成當前節點。
先回溯一次,避免連續右括號時停留在當前(節點
|
添節點
上溯，直到父是根r或(,當前節點變成自己的左節點，自己成父的右節點
&
添節點
父是|，則當前節點(0、1)成為自己的左節點，自己成父(|)的右節點
父是&，則上溯直到父是|或者根或(，當前節點成左節點，自己成父的右節點
2.遞歸計算。run函數，，先左右再根，后序遍歷，至多每個節點算一次O(n)。
return k=run(left)&&run(right);感覺只算左(不知道原因)
須要分別計算
k1=run(left)
k2=run(right)
&運算，左是0是短路。|運算左是1是短路。(當然另一邊也存在這種情況，但是本題說了只是左)
有10^6個節點

作圖驗證

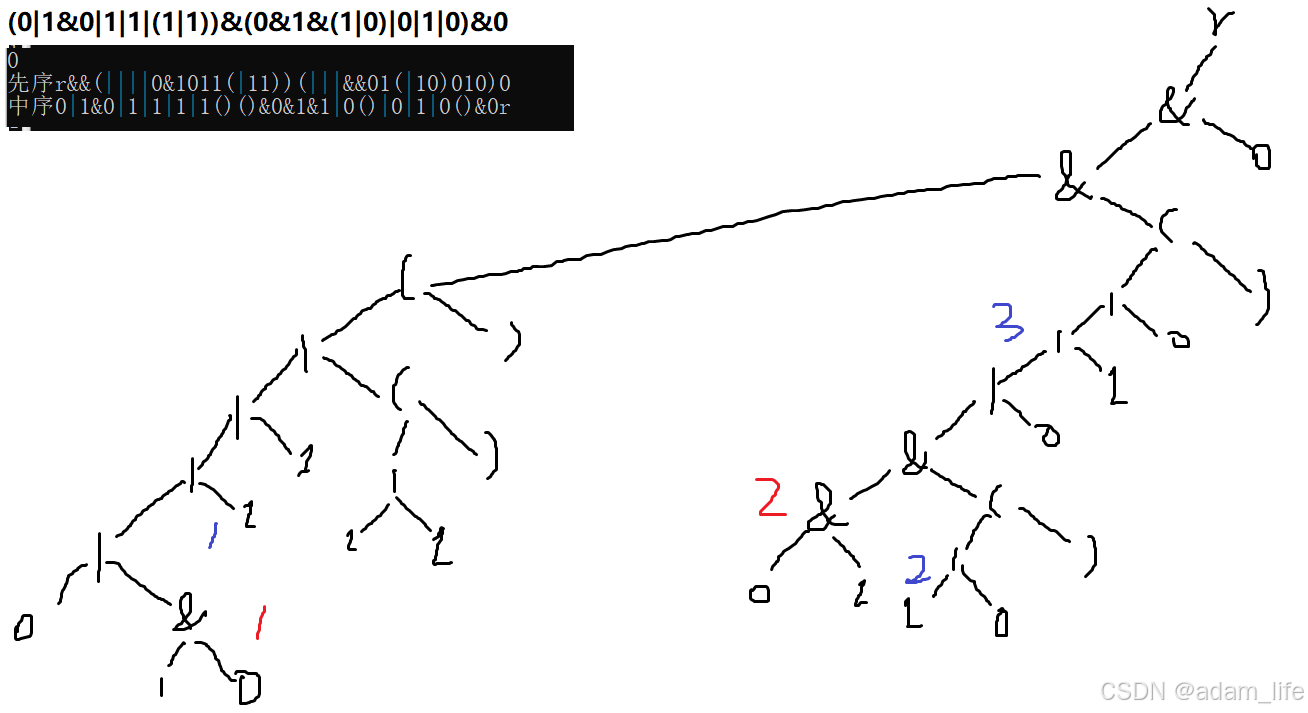
小結

冬麥需要9個月，夏玉米需要4個月。萬事萬物的生長成熟都需要足夠的時間！