在PyTorch中，nn.BatchNorm1d(128) 的作用是對 一維輸入數據（如全連接層的輸出或時間序列數據）進行批標準化（Batch Normalization），具體功能與實現原理如下：

1. 核心作用

• 標準話數據分布
  對每個批次的輸入數據進行歸一化，使其均值接近0、方差接近1，公式如下：
  $$\hat{\mathbf{x}}=\frac{\mathbf{x}?{\mu }_{batch}}{\sqrt{{\sigma }_{batch}^2+e}}$$
  其中：
  • ${\mu }_{batch}$:當前批次的均值
  • ${\sigma }_{batch}$:當前批次的方差
  • $e$: 防止除零的小常數（默認1e-5）
• 可學習的縮放與偏移：
  通過參數$\gamma$ （縮放）和 $\beta$（偏移）保留模型的表達能力：
  $$y=\gamma \hat{\mathbf{x}}+\beta$$

2. 參數解釋

3. 全連接網絡應用場景

import torch.nn as nnmodel = nn.Sequential(nn.Linear(64, 128),nn.BatchNorm1d(128),  # 對128維特征歸一化nn.ReLU(),nn.Linear(128, 10)
)

數學效果：
若輸入特征$\mathbf{x}\in {\mathbb{R}}^{m\times 128}$，輸出$y$滿足：
$$\mathbb{E}[y_{:j}]\approx 0,Var(y_{:,j})\approx 1$$

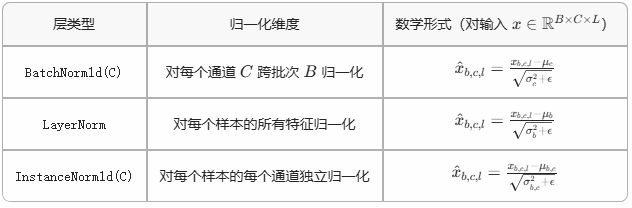
4. 與其他歸一化層的對比

5. 訓練與推理的差異

• 訓練階段
  使用當前批次的統計量${\mu }_{batch}$和${\sigma }_{batch}^2$,并更新全局統計量：
  $${\mu }_{runnning}\leftarrow {\mu }_{running}\times (1?momentum)+{\mu }_{batch}\times momentum$$
• 推理階段（測試階段）
  固定使用訓練積累的全局統計量${\mu }_{batch}$和${\sigma }_{batch}^2$
  KaTeX parse error: Undefined control sequence: \sigmma at position 54: …unning}}{\sqrt{\?s?i?g?m?m?a?^{2}_{running}+…

6. 代碼戰爭數學性質

import torch# 模擬輸入（batch_size=4, 128維特征）
x = torch.randn(4, 128) * 2 + 1  # 均值1，方差4bn = nn.BatchNorm1d(128, affine=False)  # 禁用γ和β
output = bn(x)print("輸入均值:", x.mean(dim=0).mean().item())   # ≈1
print("輸出均值:", output.mean(dim=0).mean().item())  # ≈0
print("輸入方差:", x.var(dim=0).mean().item())    # ≈4
print("輸出方差:", output.var(dim=0).mean().item())  # ≈1