一，圖的遍歷邏輯

1.之前我們學了圖的存儲，可以鄰接表存和鄰接矩陣存。現在我們要學習圖的遍歷操作和樹類似可以分為深度遍歷和廣度遍歷，而深度遍歷也是用遞歸實現，廣度遍歷是用隊列實現

2.深度遍歷(DFS)

a.確定起點

b.找到一條邊按順時針方向（準確來說存儲結構方向）來對這個節點進行處理

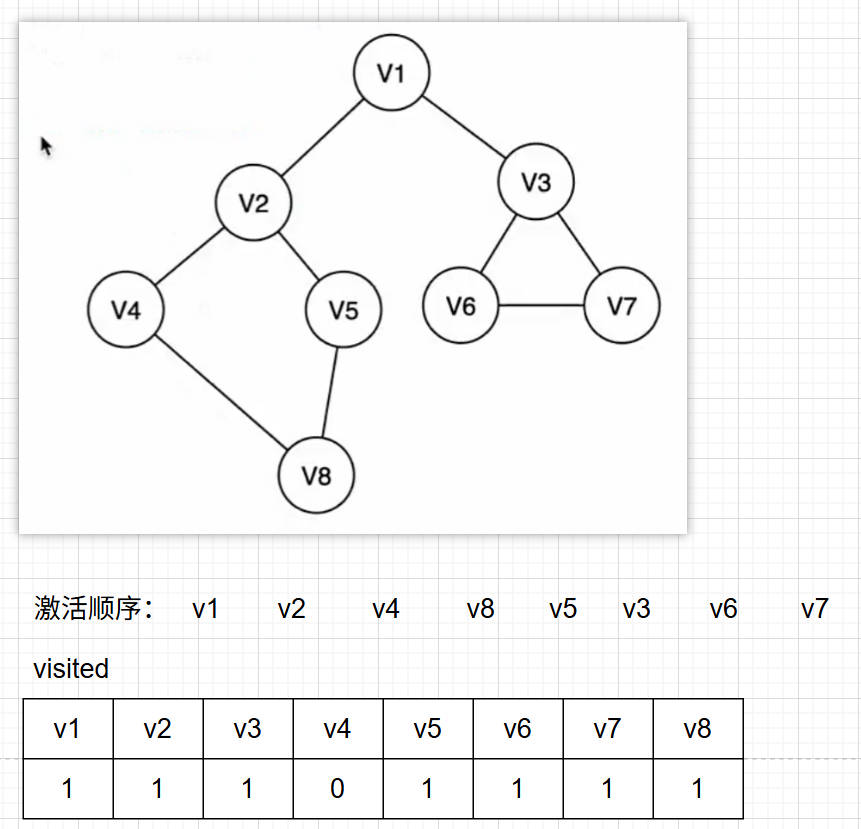如左圖當我們選擇v1為起點找到和v2的這條邊，此時激活了v2那么就需要處理v2的三條邊，但v1我們已經走過了。由于圖沒有樹那樣嚴格按照1：n的關系因此會有重復訪問的節點。因此我們可以引入一個已訪問節點的表

3.廣度遍歷（層次遍歷） (BFS)

廣度遍歷首先也是需要一個隊列，當我們訪問完一個節點就把激活的新節點入隊，然后每出隊一個節點就訪問它并把新激活的節點入隊。但是和樹不一樣，圖也是有可能重復訪問的，比如從v1開始訪問到v3，當我們訪問完v3會激活v1、v6、v7，但是v1已經被訪問過了，因此需要引入一個存儲已訪問節點的表

二，代碼實現

1.深度遍歷

static int MGraphVisited[MaxNodeNum]={0};
void DFSMGraph(MGraph *graph, int v) {//訪問節點visitMGraphNode(&graph->vex[v]);//將節點標記為已訪問MGraphVisited[v]=1;//激活連通的節點，排除已訪問的for (int i=0;i<MaxNodeNum;i++) {if (isEdge(graph->edges[v][i])&&MGraphVisited[i]==0) {//滿足條件遞歸DFSMGraph(graph,i);}}
}