LeetCode 530 二叉搜索樹的最小絕對差
題目鏈接:530. 二叉搜索樹的最小絕對差 - 力扣(LeetCode)
給你一個二叉搜索樹的根節點 root ,返回 樹中任意兩不同節點值之間的最小差值 。
差值是一個正數,其數值等于兩值之差的絕對值。
示例 1:
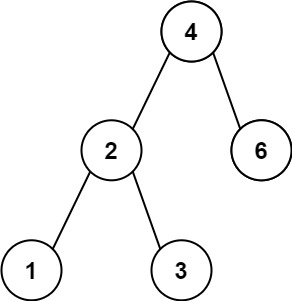
輸入:root = [4,2,6,1,3]
輸出:1
示例 2:
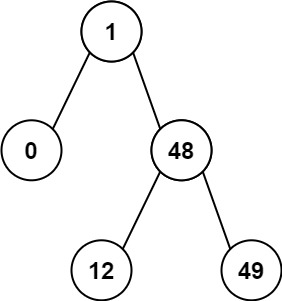
輸入:root = [1,0,48,null,null,12,49]
輸出:1
?首先將二叉搜索樹中序遍歷轉化為有序數組,其實在遍歷的過程中就可以直接計算了。
需要用一個pre節點來記錄當前節點的前一個節點。
遞歸法:
class Solution {int res=Integer.MAX_VALUE;TreeNode pre=null;public int getMinimumDifference(TreeNode root) {//遞歸if(root==null)return 0;getMinimumDifference(root.left);if(pre!=null)res=Math.min(res,root.val-pre.val);pre=root;getMinimumDifference(root.right);return res;}
}迭代法:
class Solution {public int getMinimumDifference(TreeNode root) {//迭代int res=Integer.MAX_VALUE;TreeNode pre=null;Stack<TreeNode> st=new Stack<>();st.push(root);while(!st.isEmpty()){TreeNode node=st.pop();if(node!=null){if(node.right!=null)st.push(node.right);st.push(node);st.push(null);if(node.left!=null)st.push(node.left);}else{TreeNode tmp=st.pop();if(pre!=null)res=Math.min(res,tmp.val-pre.val);pre=tmp;}}return res;}
}LeetCode 501 二叉搜索樹中的眾數
題目鏈接:501. 二叉搜索樹中的眾數 - 力扣(LeetCode)
給你一個含重復值的二叉搜索樹(BST)的根節點 root ,找出并返回 BST 中的所有 眾數(即,出現頻率最高的元素)。
如果樹中有不止一個眾數,可以按 任意順序 返回。
假定 BST 滿足如下定義:
結點左子樹中所含節點的值 小于等于 當前節點的值
結點右子樹中所含節點的值 大于等于 當前節點的值
左子樹和右子樹都是二叉搜索樹
示例 1:
輸入:root = [1,null,2,2]
輸出:[2]
示例 2:輸入:root = [0]
輸出:[0]
?最直觀的方法就是把整個樹遍歷了,用map統計頻率,把頻率排序,最后取前面高頻的元素的集合。
class Solution {public int[] findMode(TreeNode root) {Map<Integer,Integer> map=new HashMap<>();Stack<TreeNode> st=new Stack<>();if(root!=null)st.push(root);while(!st.isEmpty()){TreeNode node=st.pop();if(node!=null){if(node.right!=null)st.push(node.right);st.push(node);st.push(null);if(node.left!=null)st.push(node.left);}else{node=st.pop();if(!map.containsKey(node.val))map.put(node.val,0);else map.put(node.val,map.get(node.val)+1);}}int maxCount=0;List<Integer> list=new ArrayList<>();for(Integer obj:map.keySet()){if(map.get(obj)>maxCount)maxCount=map.get(obj);}for(Integer obj:map.keySet()){if(map.get(obj)==maxCount)list.add(obj);}int res[]=new int[list.size()];for(int i=0;i<list.size();i++){res[i]=list.get(i);}return res;}
}但既然是二叉搜索樹,它中序遍歷就是有序的,遍歷有序數組的元素出現頻率,從頭遍歷,那么一定是兩個相鄰元素作比較,然后把出現頻率最高的元素輸出就行了。
需要定義一個pre節點,是當前節點的前一個節點,每次將二者作比較。
if(pre==null)count=1;
else if(pre!=null&&tmp.val==pre.val)count++;
else count=1;
pre=tmp;
因為可能有多個眾數,所以應該要先遍歷一遍數組,找出最大頻率,然后再遍歷一遍數組把出現頻率為該最大頻率的元素放入結果中。這樣的方式需要遍歷兩次數組。
那如何只遍歷一遍呢?
如果當前元素出現頻率等于最大頻率,就把這個元素加入到結果集中;如果當前元素出現頻率大于最大頻率,先更新最大頻率,然后清空結果集,因為結果集之前的元素都失效了,然后再把當前元素加入結果集中。
完整代碼如下:
class Solution {public int[] findMode(TreeNode root) {int count=0;int maxCount=0;Stack<TreeNode> st=new Stack<>();List<Integer> list=new ArrayList<>();TreeNode pre=null;if(root!=null)st.push(root);while(!st.isEmpty()){TreeNode node=st.pop();if(node!=null){if(node.right!=null)st.push(node.right);st.push(node);st.push(null);if(node.left!=null)st.push(node.left);}else{TreeNode tmp=st.pop();if(pre==null)count=1;else if(pre!=null&&tmp.val==pre.val)count++;else count=1;pre=tmp;if(count==maxCount)list.add(tmp.val);else if(count>maxCount){maxCount=count;list.clear();list.add(tmp.val);}}}int[] res=new int[list.size()];for(int i=0;i<list.size();i++){res[i]=list.get(i);}return res;}
}遞歸寫法:
class Solution {List<Integer> list=new ArrayList<>();int count=0;int maxCount=0;TreeNode pre=null;public int[] findMode(TreeNode root) {//遞歸if(root==null)return null;findMode(root.left);if(pre==null)count=1;else if(pre!=null&&pre.val==root.val)count++;else count=1;pre=root;if(count==maxCount)list.add(root.val);else if(count>maxCount){maxCount=count;list.clear();list.add(root.val);}findMode(root.right);int[] res=new int[list.size()];for(int i=0;i<list.size();i++){res[i]=list.get(i);}return res;}
}LeetCode 236 二叉樹的最近公共祖先
題目鏈接:236. 二叉樹的最近公共祖先 - 力扣(LeetCode)
給定一個二叉樹, 找到該樹中兩個指定節點的最近公共祖先。
百度百科中最近公共祖先的定義為:“對于有根樹 T 的兩個節點 p、q,最近公共祖先表示為一個節點 x,滿足 x 是 p、q 的祖先且 x 的深度盡可能大(一個節點也可以是它自己的祖先)。”
示例 1:
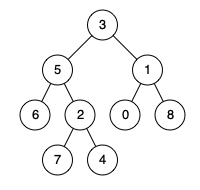
輸入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
輸出:3
解釋:節點 5 和節點 1 的最近公共祖先是節點 3 。
示例 2:
輸入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
輸出:5
解釋:節點 5 和節點 4 的最近公共祖先是節點 5 。因為根據定義最近公共祖先節點可以為節點本身。
示例 3:輸入:root = [1,2], p = 1, q = 2
輸出:1
條件:
- 樹中節點數目在范圍?
[2, 105]?內。-109 <= Node.val <= 109- 所有?
Node.val?互不相同?。p != qp?和?q?均存在于給定的二叉樹中。
?思路:首先想的是要是能自底向上查找就好了,這樣就可以找到公共祖先了。
那么如何自底向上查找?
回溯法,后序遍歷可以根據左右子樹的返回值來處理中節點的邏輯。
如何判斷一個節點是節點p和節點q的公共祖先?
如果找出一個節點,發現左子樹出現節點p,右子樹出現節點q,或者左子樹出現節點q,右子樹出現p,那么該節點就是節點p和q的最近公共祖先。
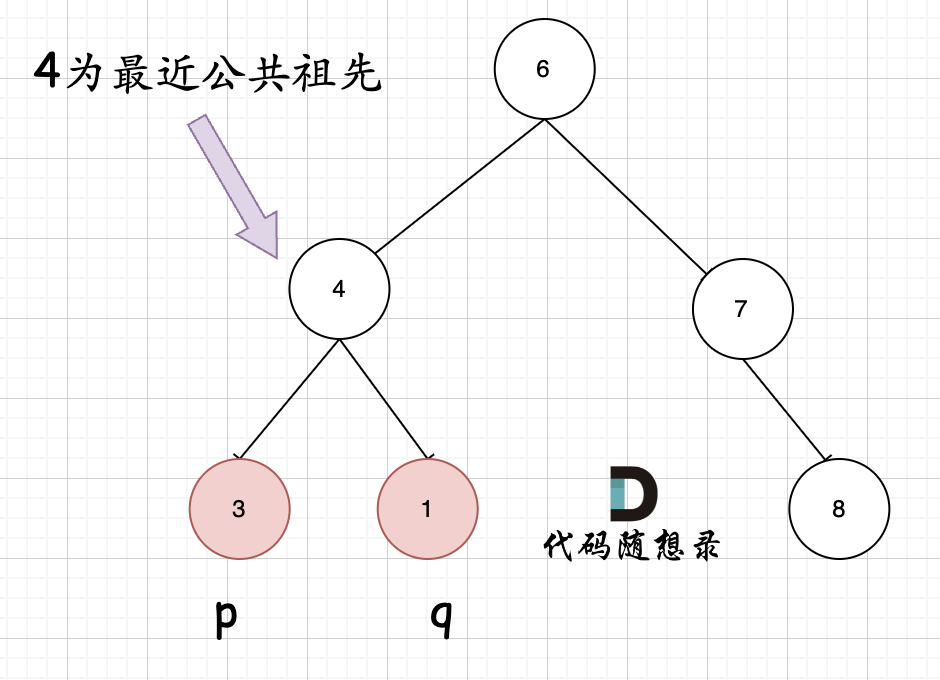
所以遞歸邏輯就是:如果遞歸遍歷遇到q,就返回q;遇到p,就返回p,那么如果左右子樹的返回值不為空,說明此時的中節點,一定是p和q的最近公共祖先。?
因為題目中說了二叉樹節點是不重復的,所以不用擔心會不會左子樹和右子樹都返回q或p這樣的問題。
實現代碼如下:
class Solution {public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {//遞歸if(root==null||root==p||root==q)return root;TreeNode left=lowestCommonAncestor(root.left,p,q);TreeNode right=lowestCommonAncestor(root.right,p,q);if(left!=null&&right!=null)return root;else if(left==null&&right!=null)return right;else if(left!=null&&right==null)return left;else return null;}
}如果left 和 right都不為空,說明此時root就是最近公共節點。這個比較好理解。
如果left為空,right不為空,就返回right,說明目標節點是通過right返回的,反之亦然。
為什么left為空,right不為空,目標節點就通過right返回?
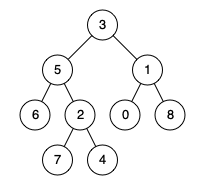
我們來看下面的圖:
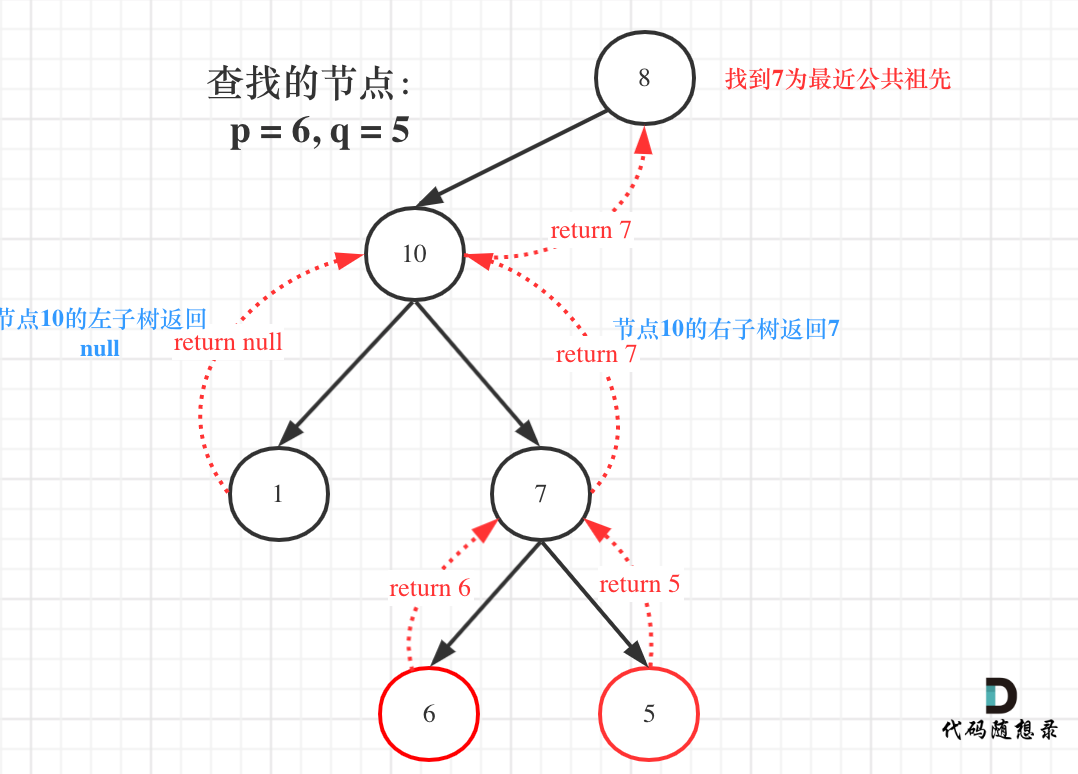
節點為10的左子樹返回null,右子樹返回7,那么此時節點10就要把右子樹的返回值返回上去。
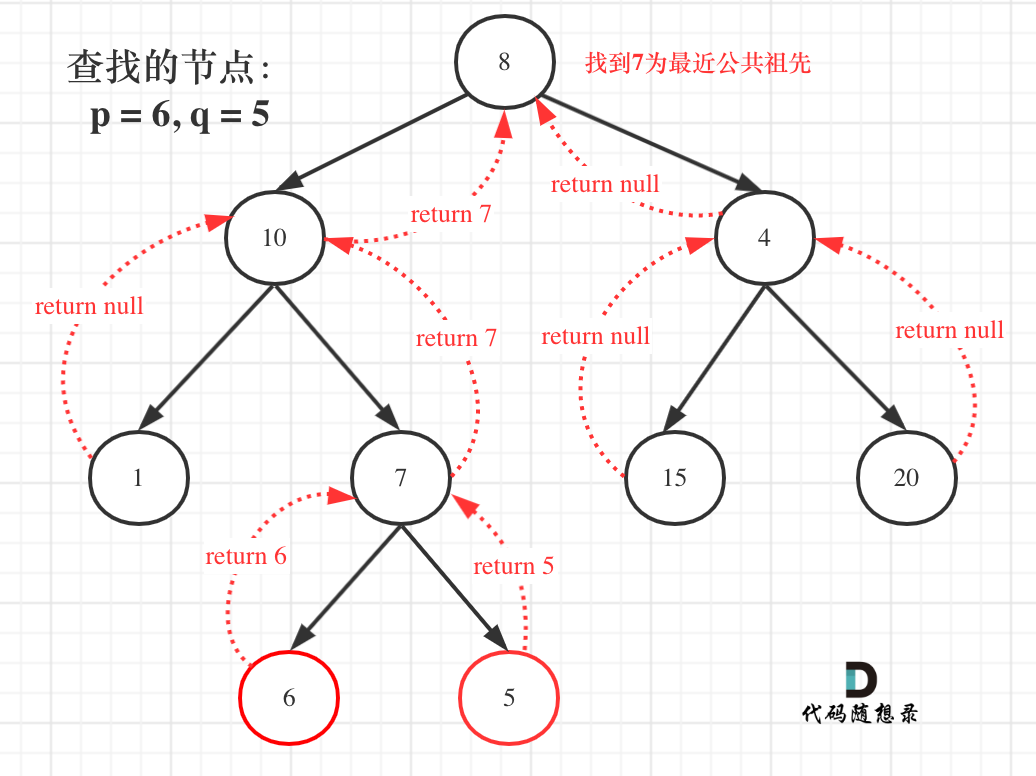
完整流程圖如下:
?




 單純享元模式和復合享元模式)


)






)




