0.理解遞歸、搜索與回溯

1.面試題 08.06.漢諾塔問題

1.1 題目

題目鏈接

1.2 思路

1.3 代碼

class Solution {
public:void hanota(vector<int>& a, vector<int>& b, vector<int>& c) {dfs(a, b, c, a.size());}void dfs(vector<int>& a, vector<int>& b, vector<int>& c, int n){if(n == 1){c.push_back(a.back());a.pop_back();return;}dfs(a, c, b, n - 1);c.push_back(a.back());a.pop_back();dfs(b, a, c, n - 1);}
};

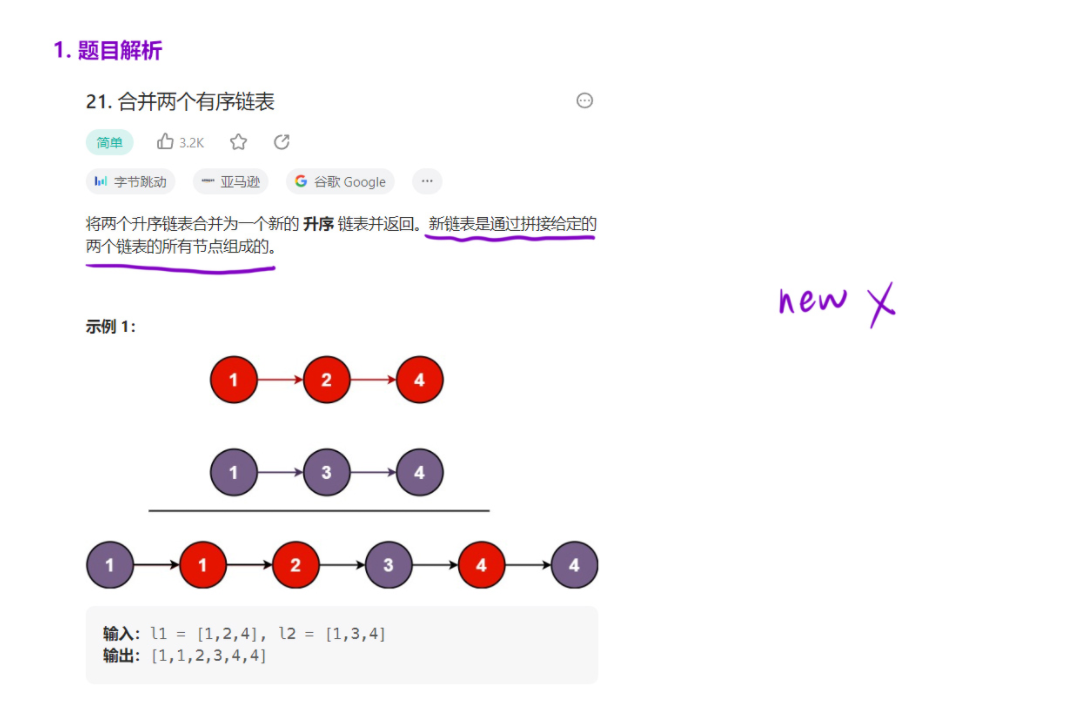
2. 合并兩個有序鏈表

2.1 題目

題目鏈接

2.2 思路

2.3 代碼

class Solution {
public:ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {if(l1 == nullptr) return l2;if(l2 == nullptr) return l1;if(l1->val < l2->val){l1->next = mergeTwoLists(l1->next, l2);return l1;}else{l2->next = mergeTwoLists(l1, l2->next);return l2;}}
};

3.反轉鏈表

3.1 題目

題目鏈接

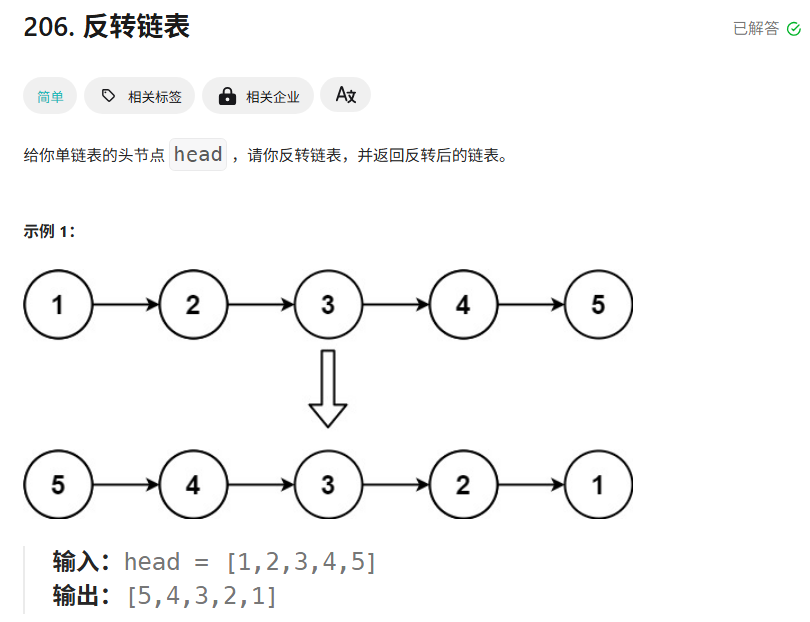
3.2 思路

3.3 代碼

class Solution {
public:ListNode* reverseList(ListNode* head) {if(head == nullptr || head->next == nullptr) return head;ListNode* newHead = reverseList(head->next);head->next->next = head;head->next = nullptr;return newHead;}
};

4.兩兩交換鏈表中的節點

4.1 題目

題目鏈接

4.2 思路

4.3 代碼

老方法-迭代

class Solution {
public:ListNode* swapPairs(ListNode* head) {if(head == nullptr || head->next == nullptr) return head;ListNode* newhead = new ListNode(0);newhead->next = head;ListNode* prev = newhead, * cur = head, * next = head->next, * nnext = next->next;while(cur && next){// 交換節點prev->next = next;next->next = cur;cur->next = nnext;// 移動prev、cur、next、nnextprev = cur;cur = nnext;if(cur) next = cur->next;if(next) nnext = next->next;}prev = newhead->next;delete newhead;return prev;}
};

新方法-遞歸

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode() : val(0), next(nullptr) {}*     ListNode(int x) : val(x), next(nullptr) {}*     ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* swapPairs(ListNode* head) {if(head == nullptr || head->next == nullptr) return head;ListNode* tmp = swapPairs(head->next->next);ListNode* newhead = head->next;head->next->next = head;head->next = tmp;return newhead;}
};

5. Pow(x, n) - 快速冪

5.1 題目

題目鏈接

5.2 思路

5.3 代碼

方法一

class Solution {
public:double myPow(double x, int N) {double ret = 1;long long int n = N;// 如果 n 是負數，將其轉換為正數（即取絕對值），并將底數 x 變為  1/xif(n < 0){n = -n;x = 1/x;}while(n){// 檢查 n 的最低位是否為 1（通過 n & 1 判斷）。如果是 1，則將當前的 x 乘到 ret 中。這是因為當前位對應的冪需要被累乘到結果中。if(n & 1)ret *= x;// 將 x 平方（即 x *= x），相當于將指數翻倍。// 將 n 右移一位（即 n >>= 1），相當于去掉當前最低位，處理下一位。x *= x;n >>= 1;}return ret;}
};

方法二 - 遞歸

class Solution {
public:double myPow(double x, int n) {// -2^31 <= n <= 2^31// 當n是負的很大的數時，會越界，所以需要將N強轉成long longreturn n > 0 ? Pow(x, n) : Pow(1/x, - (long long)n);     }double Pow(double x, int n){if(n == 0) return 1.0;double tmp = Pow(x, n/2);return n % 2 == 0 ? tmp * tmp : tmp * tmp * x;}
};