?總體引入
在計算機科學的算法領域中,排序是一項基礎且重要的操作。它旨在將一組無序的數據元素重新排列為有序序列,以滿足特定的順序要求,如升序或降序。常見的排序算法可分為不同類別,像插入排序,包含直接插入排序和希爾排序;選擇排序,有直接選擇排序和堆排序;交換排序,涵蓋冒泡排序和快速排序;還有歸并排序 。這些算法各有特點,適用于不同的應用場景,接下來讓我們深入了解它們。
?
插入排序引入
想象你整理撲克牌時,會從一堆牌里一張一張拿出來,按順序插到已經整理好的牌堆合適位置 。編程里的插入排序差不多也是這個道理。它把數據分成已排序和未排序兩部分,從 未排序部分取元素,在已排序部分找到合適位置插入,不斷重復,直到所有元素都排好序,就像把亂序的撲克牌整理成有序的一樣。

一、直接插入排序(Insertion Sort)
算法思想:
將數組分為“已排序”和“未排序”兩部分,逐個將未排序部分的元素插入到已排序部分的正確位置。
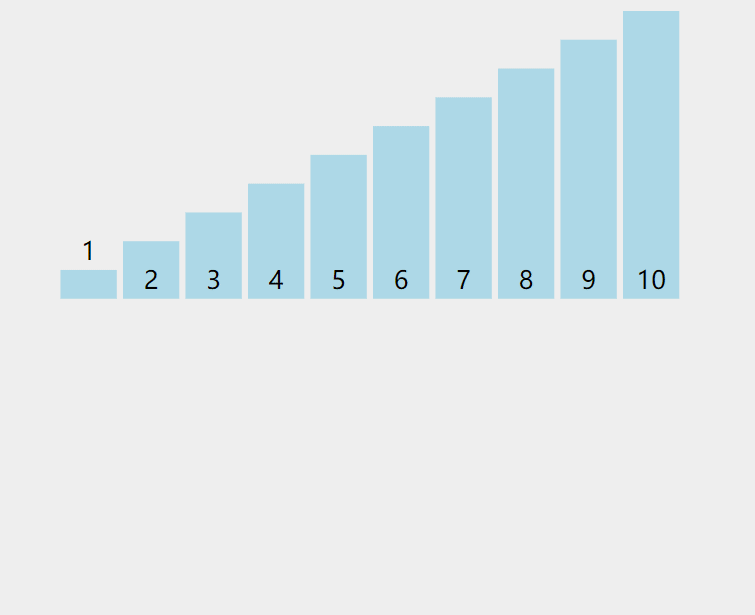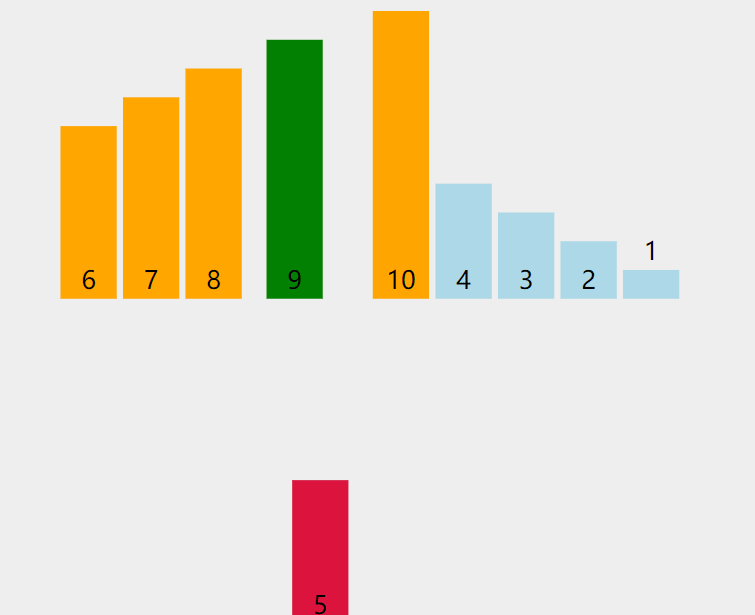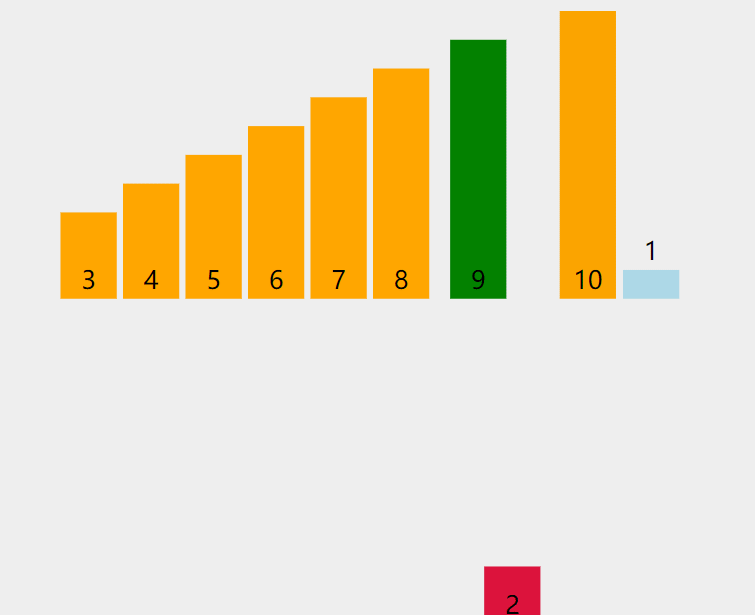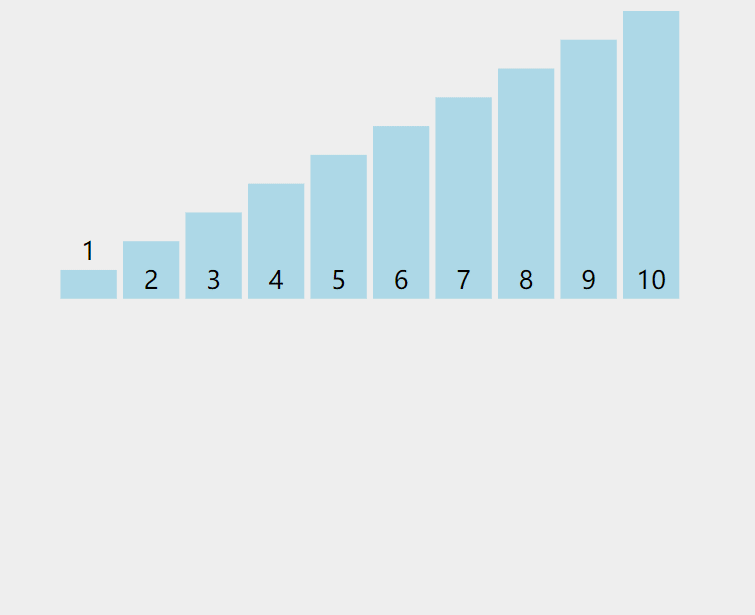
代碼解析:
void InsertSort(int* arr, int n) {for (int i = 0; i < n - 1; i++) { // 從第一個元素開始遍歷到倒數第二個元素int end = i; // 已排序部分的末尾索引int tmp = arr[end + 1]; // 待插入元素(未排序部分的第一個元素)while (end >= 0) { // 向前尋找插入位置if (arr[end] > tmp) { // 若當前元素大于待插入元素,則后移arr[end + 1] = arr[end];end--;} else { // 找到合適位置,退出循環break;}}arr[end + 1] = tmp; // 插入元素到正確位置}
}步驟說明:
-
外層循環:遍歷每個待插入元素(從第二個元素開始)。
-
內層循環:從后向前比較,若當前元素比待插入元素大,則將其后移。
-
插入操作:找到第一個比待插入元素小的位置,將元素插入其后。
復雜度分析:
-
時間復雜度:
-
最好情況(已有序):O(n),只需比較無需移動。
-
最壞情況(逆序):O(n2),每次插入需移動全部已排序元素。
-
-
空間復雜度:O(1),原地排序。
適用場景:
數據量小或基本有序時效率高,穩定且簡單。
二、希爾排序(Shell Sort)
算法思想:
希爾排序是對直接插入排序的一種改進算法,它通過將待排序的數組按照一定的間隔(稱為增量)進行分組,對每組分別進行直接插入排序,逐步縮小增量,當 gap > 1 時都是預排序,?的是讓數組更接近于有序。當 gap == 1 時,數組已經接近有序的了,這樣就會很快。這樣整體??,可以達到優化的效果。


代碼解析:
void ShellSort(int* arr, int n) {int gap = n; // 初始間隔設為數組長度while (gap > 1) { // 循環直到間隔為1(最后一次完整插入排序)gap = gap / 3 + 1; // 動態調整間隔(常見增量方式)for (int i = 0; i < n - gap; i++) { // 對所有間隔分組進行插入排序int end = i; // 當前組的已排序末尾int tmp = arr[end + gap]; // 待插入元素while (end >= 0) { // 組內插入排序if (arr[end] > tmp) { arr[end + gap] = arr[end];end -= gap; // 跨間隔移動} else {break;}}arr[end + gap] = tmp; // 插入元素}}
}步驟說明:
-
動態調整間隔:初始間隔較大,逐步縮小
(gap = gap/3 + 1)或者(gap = gap/2)。 -
分組插入排序:對每個間隔形成的子序列進行插入排序。
-
最終排序:當間隔為1時,退化為標準插入排序,此時數組已基本有序。
復雜度分析:
-
時間復雜度:約 O(n^1.3),依賴增量序列的選擇。
-
空間復雜度:O(1),原地排序。
適用場景:
中等規模數據,對穩定性無要求,優于直接插入排序。
測試案例
void test01() {int arr[] = {9, 8, 7, 6, 5, 4, 3, 2, 1, 0};int size = sizeof(arr) / sizeof(arr[0]);// InsertSort(arr, size);ShellSort(arr, size);for (int i = 0; i < size; i++) {printf("%d ", arr[i]); // 輸出:0 1 2 3 4 5 6 7 8 9}
}運行結果:
無論調用哪個排序函數,最終輸出均為有序數組 0 1 2 3 4 5 6 7 8 9。
總結
-
直接插入排序:簡單穩定,適合小數據或部分有序場景。
-
希爾排序:插入排序的高效改進,適合中等規模數據。
理解基礎排序算法的實現有助于掌握更復雜的排序技術,實際應用中可根據數據特征選擇合適的算法。






)







)


什么是裝飾器)

