前言
其實平面DP和正常的dp沒有什么本質上的區別,只不過是在二維的面上進行DP,而且,客觀的說,其實和遞推沒有什么區別,不要把他想的太難了
講解
本蒻雞思前想后,好像關于平面DP的理論知識好像沒有什么,所以我們直接上題,從題來入手
[NOIP2000 提高組] 方格取數
題目傳送門
題目背景
NOIP 2000 提高組 T4
題目描述
設有 N × N N \times N N×N 的方格圖 ( N ≤ 9 ) (N \le 9) (N≤9),我們將其中的某些方格中填入正整數,而其他的方格中則放入數字 0 0 0。如下圖所示(見樣例):
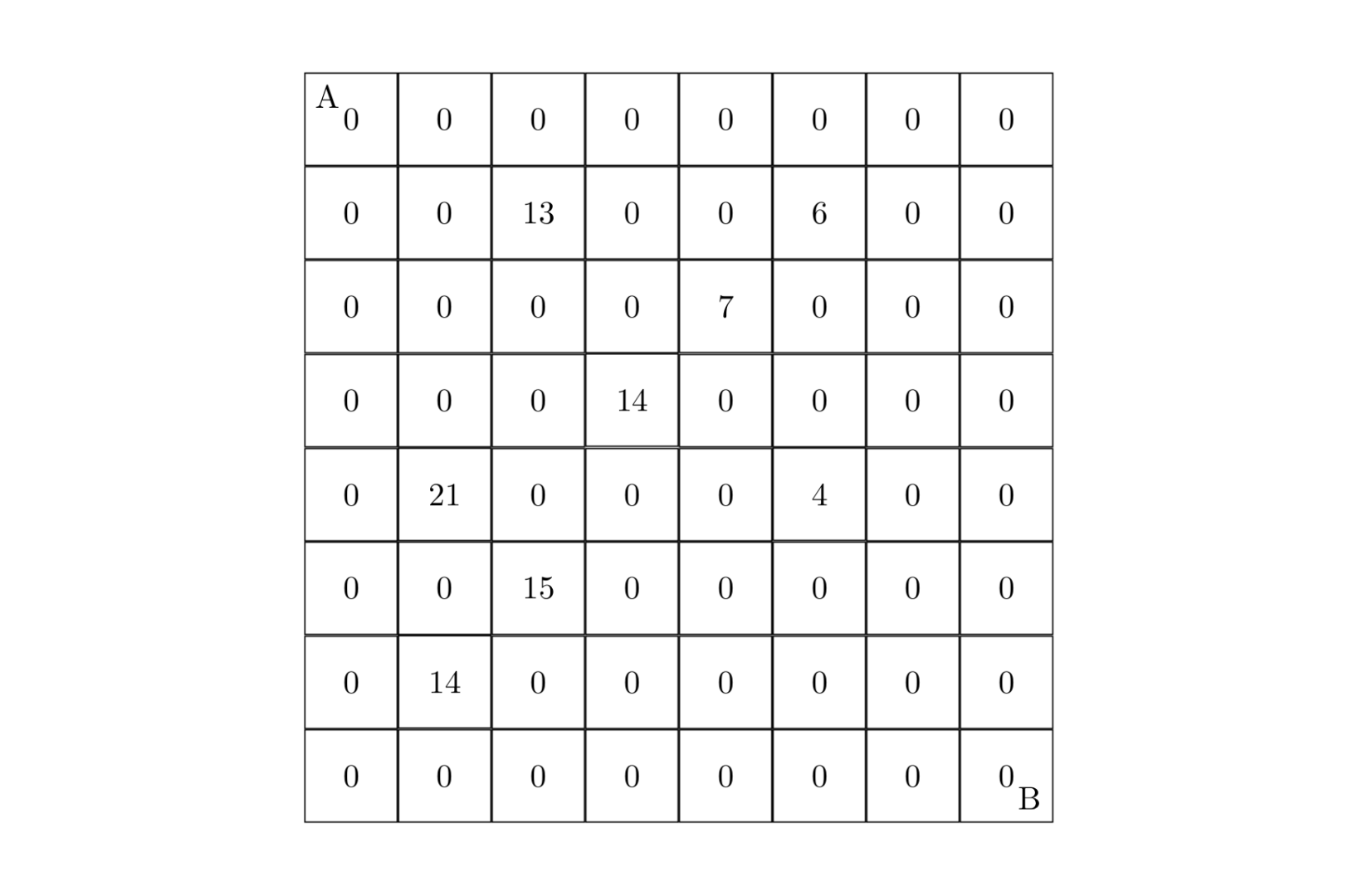
某人從圖的左上角的 A A A 點出發,可以向下行走,也可以向右走,直到到達右下角的 B B B 點。在走過的路上,他可以取走方格中的數(取走后的方格中將變為數字 0 0 0)。
此人從 A A A 點到 B B B 點共走兩次,試找出 2 2 2 條這樣的路徑,使得取得的數之和為最大。
輸入格式
輸入的第一行為一個整數 N N N(表示 N × N N \times N N×N 的方格圖),接下來的每行有三個整數,前兩個表示位置,第三個數為該位置上所放的數。一行單獨的 0 0 0 表示輸入結束。
輸出格式
只需輸出一個整數,表示 2 2 2 條路徑上取得的最大的和。
樣例 #1
樣例輸入 #1
8
2 3 13
2 6 6
3 5 7
4 4 14
5 2 21
5 6 4
6 3 15
7 2 14
0 0 0
樣例輸出 #1
67
提示
數據范圍: 1 ≤ N ≤ 9 1\le N\le 9 1≤N≤9。
思路
如果該題只取一次數或者取走一次之后原來的數還在,就是一道簡單的遞推的題,但是該題需要來回取兩次,如果我們按照貪心+遞推的思想,取完一次之后修改方格中的數,然后再取一次,那么很容易舉出反例,所以我們要思考其他辦法。
我們要知道,無論是從A–>B還是從B–>A,對于取數的答案是不會有影響的,我們不妨看做從A–>B取數取兩次,我們讓這兩次取數同時進行。
如果要同時表示表示這種狀態就需要開四維數組dp[i][j][k][l],表示分別走到點(i,j)和(k,l)的最優解。
這種的思路還是比較好想的,代碼如下
#include<bits/stdc++.h>
using namespace std;int mp[10][10],dp[10][10][10][10];
int main(){int n;cin>>n;while (1){int a,b,c;cin>>a>>b>>c;if (a==0&&b==0&&c==0)break;mp[a][b]=c;}for (int i=1;i<=n;i++){for (int j=1;j<=n;j++){for (int l=1;l<=n;l++){for (int k=1;k<=n;k++){dp[i][j][l][k]=max(max(dp[i-1][j][l-1][k],dp[i-1][j][l][k-1]),max(dp[i][j-1][l-1][k],dp[i][j-1][l][k-1]))+mp[i][j]+mp[l][k];if (i==l&&j==k)dp[i][j][l][k]-=mp[i][j];//如果相同則要減去一個}}}}cout<<dp[n][n][n][n];return 0;
}
因為這是2000年的題,那是的信息競賽的水平不高,所以范圍只有9,但是我們要有科學家鉆研的品格(我們老師的梗),所以我們來探尋一下O(n3)的方法
不難想到我們可以發現,每當我們走一步,那么x坐標和y坐標之間總會有一個數加1所以,我們可以用k來表示x坐標和y坐標的和,從而通過y坐標來計算出x坐標。由于k對于兩條同時處理的路徑可以是公共的,所以我們就可以用 f [ k ] [ y 1 ] [ y 2 ] f[k][y1][y2] f[k][y1][y2]來表示當前狀態。
#include<bits/stdc++.h>
using namespace std;int mp[700][700],dp[700][700][700];
int main(){int n;cin>>n;while (1){int a,b,c;cin>>a>>b>>c;if (a==0&&b==0&&c==0)break;mp[a][b]=c;}for (int i=1;i<=n+n;i++){for (int l=1;l<=min(i,n);l++){for (int k=1;k<=min(i,n);k++){dp[i][l][k]=max(max(dp[i-1][l-1][k],dp[i-1][l][k]),max(dp[i-1][l][k-1],dp[i-1][l-1][k-1]))+mp[i-l][l]+mp[i-k][k];if (l==k)dp[i][l][k]-=mp[i-l][l];}}}cout<<dp[n+n][n][n];return 0;
}
[NOIP2008 提高組] 傳紙條
題目傳送門
題目描述
小淵和小軒是好朋友也是同班同學,他們在一起總有談不完的話題。一次素質拓展活動中,班上同學安排坐成一個 m m m 行 n n n 列的矩陣,而小淵和小軒被安排在矩陣對角線的兩端,因此,他們就無法直接交談了。幸運的是,他們可以通過傳紙條來進行交流。紙條要經由許多同學傳到對方手里,小淵坐在矩陣的左上角,坐標 ( 1 , 1 ) (1,1) (1,1),小軒坐在矩陣的右下角,坐標 ( m , n ) (m,n) (m,n)。從小淵傳到小軒的紙條只可以向下或者向右傳遞,從小軒傳給小淵的紙條只可以向上或者向左傳遞。
在活動進行中,小淵希望給小軒傳遞一張紙條,同時希望小軒給他回復。班里每個同學都可以幫他們傳遞,但只會幫他們一次,也就是說如果此人在小淵遞給小軒紙條的時候幫忙,那么在小軒遞給小淵的時候就不會再幫忙。反之亦然。
還有一件事情需要注意,全班每個同學愿意幫忙的好感度有高有低(注意:小淵和小軒的好心程度沒有定義,輸入時用 0 0 0 表示),可以用一個 [ 0 , 100 ] [0,100] [0,100] 內的自然數來表示,數越大表示越好心。小淵和小軒希望盡可能找好心程度高的同學來幫忙傳紙條,即找到來回兩條傳遞路徑,使得這兩條路徑上同學的好心程度之和最大。現在,請你幫助小淵和小軒找到這樣的兩條路徑。
輸入格式
第一行有兩個用空格隔開的整數 m m m 和 n n n,表示班里有 m m m 行 n n n 列。
接下來的 m m m 行是一個 m × n m \times n m×n 的矩陣,矩陣中第 i i i 行 j j j 列的整數表示坐在第 i i i 行 j j j 列的學生的好心程度。每行的 n n n 個整數之間用空格隔開。
輸出格式
輸出文件共一行一個整數,表示來回兩條路上參與傳遞紙條的學生的好心程度之和的最大值。
樣例 #1
樣例輸入 #1
3 3
0 3 9
2 8 5
5 7 0
樣例輸出 #1
34
提示
【數據范圍】
對于 30 % 30\% 30% 的數據,滿足 1 ≤ m , n ≤ 10 1 \le m,n \le 10 1≤m,n≤10。
對于 100 % 100\% 100% 的數據,滿足 1 ≤ m , n ≤ 50 1 \le m,n \le 50 1≤m,n≤50。
【題目來源】
NOIP 2008 提高組第三題。
思路
這道題其實和上一道題差不多,所以我們直接寫代碼,值得注意的是,這里的每一個人都是正數,所以不用考慮走了一次后就不能走了的情況,基本上可以完全參照上一道題的寫法
#include<bits/stdc++.h>
using namespace std;long long mp[120][120],dp[120][120][120];
int main(){int n,m;cin>>n>>m;for (int i=1;i<=n;i++){for (int j=1;j<=m;j++){cin>>mp[i][j];}}for (int i=2;i<=n+m-1;i++){for (int l=1;l<=min(i,n);l++){for (int k=1;k<=min(i,n);k++){dp[i][l][k]=max(max(dp[i-1][l-1][k],dp[i-1][l][k]),max(dp[i-1][l][k-1],dp[i-1][l-1][k-1]))+mp[l][i-l+1]+mp[k][i-k+1];if (l==k)dp[i][l][k]-=mp[l][i-l+1];}}}cout<<dp[n+m-1][n][n];return 0;
}
但是話又說回來,如果這道題是有負數的呢?那么我們就要考慮如何排除又重復的情況了。其實解題思路是一樣的,只是狀態轉移方程不同,既然兩條路徑不能重疊,那么一定有一條路徑在上上,一條路徑在下方,這里我們始終讓i<j就行了,但是注意特判起點和終點。
#include<bits/stdc++.h>
using namespace std;long long mp[220][220],dp[420][220][220];
int main(){int n,m;cin>>n>>m;for (int i=1;i<=n;i++){for (int j=1;j<=m;j++){cin>>mp[i][j];}}dp[2][1][1]=mp[1][1];for (int i=2;i<=n+m;i++){for (int j=0;j<=n;j++){for (int k=0;k<=n;k++){dp[i][j][k]=INT_MIN;}}}dp[2][1][1]=mp[1][1];for (int i=2;i<=n+m;i++){for (int l=1;l<=n&&l<i;l++){for (int k=1;k<min(l,i);k++){dp[i][l][k]=max(max(dp[i-1][l-1][k],dp[i-1][l][k]),max(dp[i-1][l][k-1],dp[i-1][l-1][k-1]))+mp[l][i-l]+mp[k][i-k];}}}dp[n+m][n][n]=dp[n+m-1][n][n-1]+mp[n][m];cout<<dp[n+m][n][n];return 0;
}
最大加權矩形
題目傳送門
題目描述
為了更好的備戰 NOIP2013,電腦組的幾個穿黑絲的女孩子 LYQ,ZSC,ZHQ 認為,我們不光需要機房,我們還需要運動,于是就決定找校長申請一塊電腦組的課余運動場地,聽說她們都是電腦組的高手,校長沒有馬上答應他們,而是先給她們出了一道數學題,并且告訴她們:你們能獲得的運動場地的面積就是你們能找到的這個最大的數字。
校長先給他們一個 n × n n\times n n×n 矩陣。要求矩陣中最大加權矩形,即矩陣的每一個元素都有一權值,權值定義在整數集上。從中找一矩形,矩形大小無限制,是其中包含的所有元素的和最大 。矩陣的每個元素屬于 [ ? 127 , 127 ] [-127,127] [?127,127] ,例如
0 –2 –7 0 9 2 –6 2
-4 1 –4 1
-1 8 0 –2
在左下角:
9 2
-4 1
-1 8
和為 15 15 15。
幾個女孩子有點犯難了,于是就找到了電腦組精打細算的 HZH,TZY 小朋友幫忙計算,但是遺憾的是他們的答案都不一樣,涉及土地的事情我們可不能含糊,你能幫忙計算出校長所給的矩形中加權和最大的矩形嗎?
輸入格式
第一行: n n n,接下來是 n n n 行 n n n 列的矩陣。
輸出格式
最大矩形(子矩陣)的和。
樣例 #1
樣例輸入 #1
4
0 -2 -7 09 2 -6 2
-4 1 -4 1
-1 8 0 -2
樣例輸出 #1
15
提示
1 ≤ n ≤ 120 1 \leq n\le 120 1≤n≤120
首先可以看到這道題的數據范圍似乎不是很大,好像O(n4)就可以過,那么我們就先這樣去想想,是不是可以利用前綴和呢?答案是可以的,代碼如下
#include<iostream>
using namespace std;
int n,mx=INT_MIN;
int a[130][130],sum[130][130],qz[130][130];
int main(){cin>>n;for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){cin>>a[i][j];qz[i][j]=qz[i][j-1]+a[i][j];sum[i][j]=qz[i][j]+sum[i-1][j];}}for(int x1=1;x1<=n;x1++){for(int y1=1;y1<=n;y1++){for(int x2=1;x2<=n;x2++){for(int y2=1;y2<=n;y2++){if (x2<x1||y2<y1)continue;mx=max(mx,sum[x2][y2]+sum[x1-1][y1-1]-sum[x2][y1-1]-sum[x1-1][y2]);}}}}cout<<mx;return 0;
}
但是我們再想想,如果數據再大一點怎么辦呢?請聽下回分解~~~~





)



Develop Team)





)





