算法題型歸類整理及同類題型解法思路總結（持續更新）

1、最優路線

通用思路

1、遞歸

#案例1-最優路測路線

題目描述

評估一個網絡的信號質量，其中一個做法是將網絡劃分為柵格，然后對每個柵格的信號質量計算。

路測的時候，希望選擇一條信號最好的路線（彼此相連的柵格集合）進行演示。

現給出 R 行 C 列的整數數組 Cov，每個單元格的數值 S 即為該柵格的信號質量（已歸一化，無單位，值越大信號越好）。

要求從 [0, 0] 到 [R-1, C-1]設計一條最優路測路線。返回該路線得分。

規則：

路測路線可以上下左右四個方向，不能對角
路線的評分是以路線上信號最差的柵格為準的，例如路徑 8→4→5→9 的值為4，該線路評分為4。線路最優表示該條線路的評分最高。

輸入描述

一行表示柵格的行數 R

第二行表示柵格的列數 C

第三行開始，每一行表示柵格地圖一行的信號值，如5 4 5

輸出描述

最優路線的得分

備注

1 ≤ R，C ≤ 20
0 ≤ S ≤ 65535

用例1

輸入

輸出

說明

路線為：5→4→5→6→6

用例2

輸入

輸出

說明

路線為：3→4→6→3→4→7→7→8→9→4→3→8→8→3→4→4→6→5→4→3

代碼：

package algorithm.huawei;import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.Scanner;public class Test61ZuiyouLuxian {static int min = Integer.MAX_VALUE;static List<List<Path>> ll = new ArrayList<List<Path>>();public static void main(String[] args) {Scanner in = new Scanner(System.in);while (in.hasNextInt()) {int m = in.nextInt();in.nextLine();int n = in.nextInt();int[][] mn = new int[m][n];for(int i=0;i<m;i++){for(int j=0;j<n;j++){mn[i][j] = in.nextInt();}in.nextLine();}int min=mn[0][0];List<Integer> li = new LinkedList<Integer>();
//			數據準備完畢dfs(mn,m,n,0,0,min,li);System.out.println(li.get(0));}}private static void dfs(int[][] mn, int m, int n, int i, int j, int min, List<Integer> li) {if(i<0 || j<0 || i>m-1 || j>n-1 || mn[i][j]==-1){return;}if(li.size()>0 && min<=li.get(0)){return;}min = Math.min(min, mn[i][j]);if(i==m-1 && j==n-1){li.clear();li.add(min);}int temp=mn[i][j];mn[i][j] = -1;//禁止走回頭路dfs(mn,m,n,i-1,j,min,li);//向上dfs(mn,m,n,i+1,j,min,li);//向下dfs(mn,m,n,i,j-1,min,li);//向左dfs(mn,m,n,i,j+1,min,li);//向右mn[i][j] = temp;//回溯		}}

#案例2-可以組成網絡的服務器

在一個機房中，服務器的位置標識在n*m的整數矩陣網格中，1表示單元格上有服務器，0表示沒有。如果兩臺服務器位于同一行或者同一列中緊鄰的位置，則認為它們之間可以組成一個局域網，請你統計機房中最大的局域網包含的服務器個數。

輸入描述

第一行輸入兩個正整數，n和m，0<n,m<=100

之后為n*m的二維數組，代表服務器信息

輸出描述

最大局域網包含的服務器個數。

示例1

輸入：
2 2
1 0
1 1輸出：
3說明： [0][0]、[1][0]、[1][1] 三臺服務器互相連接，可以組成局域網。

代碼：

思路：

1）上下左右搜索，被搜索到的位置更新為0。

2）該題也可以使用并查集實現。【代碼附后方】

package algorithm.huawei;import java.util.Scanner;
/*案例：
3 6
1 0 1 1 0 1
1 1 1 0 0 1
1 0 1 1 0 1
9*/
/*
3 6
1 0 1 1 1 0
1 1 1 0 0 1
1 0 1 1 0 1
10*/
public class Test24Tu {public static void main(String[] args) {Scanner in = new Scanner(System.in);while (in.hasNextInt()) {int n = in.nextInt();int m = in.nextInt();in.nextLine();int[][] mn = new int[n][m];for(int i=0;i<n;i++){for(int j=0;j<m;j++){mn[i][j] = in.nextInt();}in.nextLine();}int max=0;for(int i=0;i<n;i++){for(int j=0;j<m;j++){if(mn[i][j]==0){continue;}max = Math.max(max, dfs(mn,m,n,i,j));}}System.out.println(max);}}private static int dfs(int[][] mn, int m, int n, int x, int y) {if(x<0 || y<0 || x>=n || y>=m || mn[x][y]==0){return 0;}int cnt=0;if(mn[x][y]==1){cnt=1;mn[x][y]=0;}int up=dfs(mn,m,n,x-1,y);//向上int down=dfs(mn,m,n,x+1,y);//向下int left=dfs(mn,m,n,x,y-1);//向左int right=dfs(mn,m,n,x,y+1);//向右return up+down+left+right+cnt;}}

package algorithm.huawei;import java.util.Arrays;
import java.util.Scanner;
/*案例：
3 6
1 0 1 1 0 1
1 1 1 0 0 1
1 0 1 1 0 1
9*/
/*
3 6
1 0 1 1 1 0
1 1 1 0 0 1
1 0 1 1 0 1
10*/
public class Test24Tu {public static void main(String[] args) {Scanner in = new Scanner(System.in);while (in.hasNextInt()) {int n = in.nextInt();int m = in.nextInt();in.nextLine();int[][] mn = new int[n][m];for(int i=0;i<n;i++){for(int j=0;j<m;j++){mn[i][j] = in.nextInt();}in.nextLine();}
//================方案1：遞歸求解====================//	/*int max=0;for(int i=0;i<n;i++){for(int j=0;j<m;j++){if(mn[i][j]==0){continue;}max = Math.max(max, dfs(mn,m,n,i,j));}}System.out.println(max);*///================方案2：并查集求解====================//			int[] us = new int[n*m];Arrays.fill(us, -1);for(int i=0;i<n;i++){for(int j=0;j<m;j++){int index=i*m+j;//數組下標if(mn[i][j]==1){boolean left = (j-1>=0 && mn[i][j-1]==1);//左側是否有1boolean up = (i-1>=0 && mn[i-1][j]==1);//上側是否有1if(left && up){//如果都有則進行合并,將上邊并查集合到左邊//找到左側的根int rootL = findRoot(us,index-1);//找到上側的根int rootU = findRoot(us,(i-1)*m+j);us[rootL]=us[rootL]+us[rootU]-1;us[rootU]=rootL;us[index] = rootL;}else if(left){//只有左側有則合并到左側//找到左側的根int root = findRoot(us,index-1);us[root]-=1;us[index] = root;}else if(up){//只有上側有則合并到上側//找到上側的根int root = findRoot(us,(i-1)*m+j);us[root]-=1;us[index] = root;}else{//都沒有則自己是新并查集的根us[index] = -1;}}}}int min=0;for(int i=0;i<us.length;i++){if(us[i]<0){min = Math.min(min, us[i]);}}System.out.println(-min);}}private static int findRoot(int[] us, int i) {while(us[i]>=0){i=us[i];}return i;}private static int dfs(int[][] mn, int m, int n, int x, int y) {if(x<0 || y<0 || x>=n || y>=m || mn[x][y]==0){return 0;}int cnt=0;if(mn[x][y]==1){cnt=1;mn[x][y]=0;}int up=dfs(mn,m,n,x-1,y);//向上int down=dfs(mn,m,n,x+1,y);//向下int left=dfs(mn,m,n,x,y-1);//向左int right=dfs(mn,m,n,x,y+1);//向右return up+down+left+right+cnt;}}

2、最長子串

滑動窗口、狀態打標

#案例1-出現偶數次最長子字符串的長度

題目描述

給你一個字符串 s，字符串 s 首尾相連成一個環形，請你在環中找出 'l'、'o'、'x' 字符都恰好出現了偶數次最長子字符串的長度。

輸入描述

輸入是一串小寫的字母組成的字符串

輸出描述

輸出是一個整數

1 ≤ s.length ≤ 5 * 10^5

s只包含小寫英文字母

代碼：

package algorithm.huawei;import java.util.Scanner;//思路
//經典的狀態壓縮動態規劃, 一般遇到要保存的狀態不多的問題時都可以通過狀態壓縮來解決
//注意到元音字母只有 5 個, 所以根據不同字母的奇偶性總共也就 32 個狀態
//狀態為 0 時代表[0,0,0,0,0], 表示所有元音字母都有偶數個
//狀態為 1 時代表[0,0,0,0,1], 表示只有 a 是奇數, 其余字母有偶數個
//狀態為 2 時代表[0,0,0,1,0], 表示只有 e 是奇數, 其余字母有偶數個
//...
//狀態為 31 時代表[1,1,1,1,1], 表示所有元音字母都有奇數個
//可以利用這一點, 存不同狀態下的最左邊下標, 并保存當前的狀態, 初始化狀態為 0, 因為此時各個元音字母都是 0 個, 即偶數個
//如果當前下標 i 對應的狀態已經有最左下標 j 了, 那么[j+1,i]這段區間的各個元音字母的數目一定是偶數個, 這樣才能保證 i 和 j 處的狀態相同, 如果其長度大于結果值就更新結果即可
//特別注意當狀態為 0 時本身就是合法的, 長度就是當前下標+1, 所以可以初始化該狀態的下標為-1, 這樣就可以和其他狀態下的邏輯一致了
//
public class Test12ZichuanChangdu {public static void main(String[] args) {Scanner sc = new Scanner(System.in);String input = sc.nextLine();System.out.println(getResult(input));}public static int getResult(String s) {int index = 0b000;
//    	每個下標代表一個狀態，值代表符合該狀態的第一個元素的下標int[] status = new int[8];status[0]=-1;int maxLen = 0;for (int i = 0; i < s.length() * 2; i++) {char c = s.charAt(i % s.length());switch (c) {case 'l':index ^= 0b100;break;case 'o':index ^= 0b010;break;case 'x':index ^= 0b001;break;}if (status[index] == 0) {status[index] = i;}else{maxLen = Math.max(maxLen, i-status[index]<=s.length()?i-status[index]:maxLen);}}return maxLen;}}

3、最長公共子串

動態規劃

4、最長序列

線段樹

5、四則運算

棧

6、進出問題

通用思路

隊列、棧、雙端隊列

#案例1-籃球游戲

幼兒園里有一個放倒的圓桶，它是一個線性結構，允許在桶的右邊將籃球放入，可以在桶的左邊和右邊將籃球取出。

每個籃球有單獨的編號，老師可以連續放入一個或多個籃球，小朋友可以在桶左邊或右邊將籃球取出，當桶里只有一個籃球的情況下，必須從左邊取出。

如老師按順序放入1、2、3、4、5 共5個編號的籃球，那么小朋友可以依次取出的編號為“1,2,3,4,5”或者“3,1,2,4,5”編號的籃球，無法取出 “5,1,3,2,4” 編號的籃球。

其中“3,1,2,4,5”的取出場景為：

連續放入1,2,3號
從右邊取出3號
從左邊取出1號
從左邊取出2號
放入4號
從左邊取出4號
放入5號
從左邊取出5號

簡單起見，我們以L表示左，R表示右，此時的籃球的依次取出序列為“ RLLLL ”

輸入描述

1、第一行的數字作為老師依次放入的籃球編號；

2、第二行的數字作為要檢查是否能夠按照放入順序取出的籃球編號；

其中籃球編號用逗號進行分隔。

輸出描述

對于每個籃球的取出序列，如果確實可以獲取，請打印出其按照左右方向的操作的取出順序，如果無法獲取則打印"NO" 。

補充說明：

1<=籃球的編號，籃球個數<=200；
籃球上的數字不重復；
輸出的結果中LR的必須為大寫；

示例1

輸入：
4,5,6,7,0,1,2
6,4,0,1,2,5,7輸出：
RLRRRLL說明：
籃球的取出順序依次為 “右，左，右，右，右，左，左”

示例2

輸入：
4,5,6,7,0,1,2
6,0,5,1,2,4,7輸出：
NO說明：
無法取出對應序列的籃球

示例3

輸入：
1,2,3,4
1,2,3,5輸出：
NO說明：
不存在編號為5的籃球，所以無法取出對應的編號數據

代碼：

package algorithm.huawei;import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.Deque;
import java.util.LinkedList;
import java.util.List;
import java.util.Scanner;public class Test126 {public static void main(String[] args) {Scanner in = new Scanner(System.in);while (in.hasNextLine()) {String[] sa = in.nextLine().split(",");Deque<Integer> que = new ArrayDeque<Integer>();for(int i=0;i<sa.length;i++){que.offer(Integer.parseInt(sa[i]));}String[] sa2 = in.nextLine().split(",");List<Integer> take = new ArrayList<Integer>();for(int i=0;i<sa2.length;i++){take.add(Integer.parseInt(sa2[i]));}LinkedList<Integer> ll = new LinkedList<Integer>();int takeIndex = 0;StringBuilder sb = new StringBuilder();while(!que.isEmpty() || ll.size()>0){while(que.size()>0 && (ll==null || !ll.contains(take.get(takeIndex)))){ll.add(que.poll());}if(ll.peekFirst()==take.get(takeIndex)){sb.append("L");ll.pollFirst();}else if(ll.peekLast()==take.get(takeIndex)){sb.append("R");ll.pollLast();}else{sb=new StringBuilder("NO");break;}takeIndex++;}System.out.println(sb.toString());}}}

#案例2-火車進出站

給定一個正整數N代表火車數量，0<N<10，接下來輸入火車入站的序列，一共N輛火車，每輛火車以數字1-9編號，火車站只有一個方向進出，同時停靠在火車站的列車中，只有后進站的出站了，先進站的才能出站。

要求輸出所有火車出站的方案，以字典序排序輸出。

數據范圍：1≤n≤10?

進階：時間復雜度：O(n!)?，空間復雜度：O(n)?

輸入描述：

第一行輸入一個正整數N（0 < N <= 10），第二行包括N個正整數，范圍為1到10。

輸出描述：

輸出以字典序從小到大排序的火車出站序列號，每個編號以空格隔開，每個輸出序列換行，具體見sample。

示例1

輸入：

3
1 2 3

復制輸出：

復制說明：

第一種方案：1進、1出、2進、2出、3進、3出
第二種方案：1進、1出、2進、3進、3出、2出
第三種方案：1進、2進、2出、1出、3進、3出
第四種方案：1進、2進、2出、3進、3出、1出
第五種方案：1進、2進、3進、3出、2出、1出
請注意，[3,1,2]這個序列是不可能實現的。

代碼：

import java.util.*;
// 隊列表示未進站的火車
// 棧表示已進站的火車
// 每次火車進站后有兩種選擇：1.直接出站 2.等待下列火車進站  使用遞歸考慮
// 記錄和打印的遞歸函數往往是void，如果遞歸完成后還存在后續邏輯，一般情況下當前輸入變量不應受到遞歸的影響（所以當函數參數為引用類型時，遞歸的參數應當重新new出來或者深拷貝出來）
public class Main {public static void main(String[] args) {Scanner sc = new Scanner(System.in);while (sc.hasNext()) {int n = sc.nextInt();// 未進站的火車Queue<Integer> queue = new LinkedList<>();// 已進站的火車Stack<Integer> stack = new Stack<>();for (int i = 0; i < n; i++) {queue.offer(sc.nextInt());}List<String> outQueueList = new ArrayList<>();// 獲取所有出站隊列保存到outQueueListprocessOutQueue(queue, stack, "", outQueueList);// 排序Collections.sort(outQueueList);for (String str : outQueueList) {System.out.println(str);}}}private static void processOutQueue(Queue<Integer> queue, Stack<Integer> stack,String outQueue, List<String> outQueueList) {// 如果隊列和棧都為空，則保存出站信息if (queue.isEmpty() && stack.isEmpty()) {outQueueList.add(outQueue.trim());return;}// 二：進棧if (!queue.isEmpty()) {// 先克隆,這里全部克隆的原因是因為遞歸完回來后，不能影響我的第二種選擇// processOutQueue前面的邏輯，遞歸越深的越晚執行；processOutQueue后面的代碼（下方的出棧代碼）遞歸越深的越先執行Queue<Integer> tempQueue = new LinkedList<>(queue);Stack<Integer> tempStack = (Stack<Integer>) stack.clone();tempStack.push(tempQueue.poll());processOutQueue(tempQueue, tempStack, outQueue, outQueueList);}// 隊列和棧有兩種情況：出棧或進棧// 一：出棧if (!stack.isEmpty()) {// 先克隆Queue<Integer> tempQueue = new LinkedList<>(queue);Stack<Integer> tempStack = (Stack<Integer>) stack.clone();String tempOutQueue = outQueue + (tempStack.pop() + " ");processOutQueue(tempQueue, tempStack, tempOutQueue, outQueueList);}}
}

7、最大匹配數問題

通用思路

匈牙利匹配算法（先到先得，能讓則讓）

#案例1-素數伴侶

題目描述
若兩個正整數的和為素數，則這兩個正整數稱之為“素數伴侶”，如2和5、6和13，它們能應用于通信加密。現在密碼學會請你設計一個程序，從已有的 N （ N 為偶數）個正整數中挑選出若干對組成“素數伴侶”，挑選方案多種多樣，例如有4個正整數：2，5，6，13，如果將5和6分為一組中只能得到一組“素數伴侶”，而將2和5、6和13編組將得到兩組“素數伴侶”，能組成“素數伴侶”最多的方案稱為“最佳方案”，當然密碼學會希望你尋找出“最佳方案”。

輸入:

有一個正偶數 n ，表示待挑選的自然數的個數。后面給出 n 個具體的數字。

輸出:

輸出一個整數 K ，表示你求得的“最佳方案”組成“素數伴侶”的對數。

數據范圍：?1≤n≤100??，輸入的數據大小滿足 2≤val≤30000?

輸入描述：

輸入說明
1?輸入一個正偶數 n
2?輸入 n 個整數

輸出描述：

求得的“最佳方案”組成“素數伴侶”的對數。

示例1

輸入：

4
2 5 6 13

復制輸出：

復制

示例2

輸入：

2
3 6

復制輸出：

代碼：

import java.util.*;// 注意類名必須為 Main, 不要有任何 package xxx 信息
// 遇到遞歸出現在循環里面的，終止條件則是想辦法讓越深層的遞歸循環次數越少，直到一次循環條件都不滿足則返回默認的值
public class Main {public static void main(String[] args) {Scanner in = new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的區別while (in.hasNextInt()) { // 注意 while 處理多個 caseint n = in.nextInt();in.nextLine();// 奇數數組List<Integer> odds = new ArrayList<Integer>();// 偶數數組List<Integer> events = new ArrayList<Integer>();for(int i=0;i<n;i++){int var = in.nextInt();if(var%2 == 0){events.add(var);}else{odds.add(var);}}int count = 0;int[] ifMatch = new int[events.size()];for(int i=0;i<odds.size();i++){boolean[] canuse = new boolean[events.size()];Arrays.fill(canuse,true);if(dfs(odds.get(i),events,ifMatch,canuse)){count++;};}System.out.println(count);}}public static boolean dfs(int x,List<Integer> events,int[] ifMatch,boolean[] canuse) {for(int i=0;i<events.size();i++){// 先到先得:如果該位置能用且符合素數且該位置沒被占用則可以占用if(canuse[i] && isPrime(x+events.get(i))){canuse[i] = false;//把位置改為不可用if(ifMatch[i]==0 || dfs(ifMatch[i],events,ifMatch,canuse)){//如果該位置沒被占用，或者被占用了但是占用的odd能重新找到其他event進行匹配，則可以使用ifMatch[i] = x;return true;}}}return false;}public static boolean isPrime(int x) {for(int i=2;i<=Math.sqrt(x);i++){if(x%i==0){return false;}}return true;}
}

#案例2-矩陣匹配

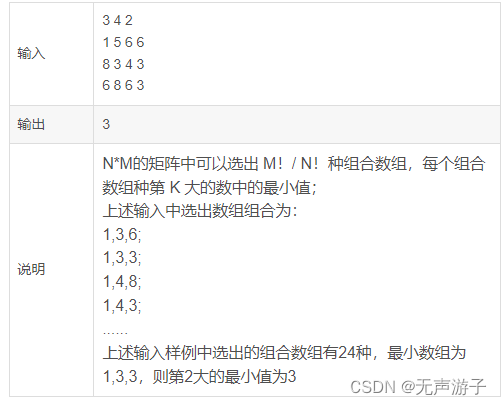
題目描述

從一個 N * M（N ≤ M）的矩陣中選出 N 個數，任意兩個數字不能在同一行或同一列，求選出來的 N 個數中第 K 大的數字的最小值是多少。

輸入描述

輸入矩陣要求：1 ≤ K ≤ N ≤ M ≤ 150

輸入格式：

N M K

N*M矩陣

輸出描述

N*M 的矩陣中可以選出 M! / N! 種組合數組，每個組合數組種第 K 大的數中的最小值。無需考慮重復數字，直接取字典排序結果即可。

備注

注意：結果是第 K 大的數字的最小值

代碼：

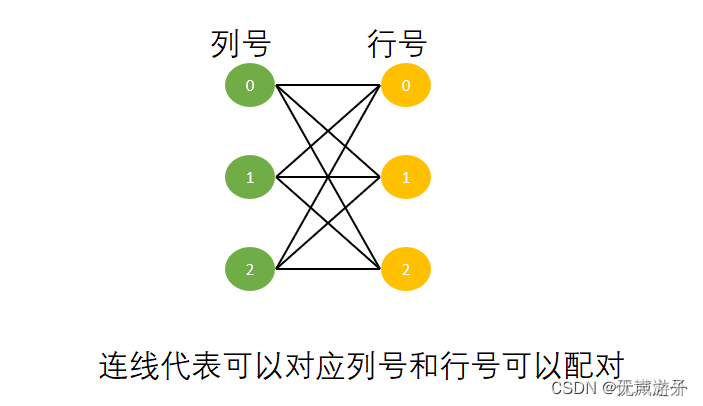
思路：每一個行號只能跟一個列號匹配，我們可以利用二分法枚舉第k大的值，然后通過匈牙利算法檢查符合條件的且小于這個值的匹配數量是否滿足要求，如果滿足則說明枚舉值kth給大了，如果不滿足說明枚舉值kth給小了。

import java.util.Arrays;
import java.util.Scanner;public class Main {static int n;static int m;static int k;static int[][] matrix;public static void main(String[] args) {Scanner sc = new Scanner(System.in);n = sc.nextInt();m = sc.nextInt();k = sc.nextInt();int min = 1;int max = Integer.MIN_VALUE;matrix = new int[n][m];for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {matrix[i][j] = sc.nextInt();max = Math.max(max, matrix[i][j]);}}// 二分枚舉第K大值while (min <= max) {// mid就是被枚舉出來的N個數中的第K大值int mid = (min + max) >> 1;// 檢查mid作為N個數中第K大值時，是否存在N-K+1個不大于它的值if (check(mid)) {max = mid - 1;} else {min = mid + 1;}}System.out.println(min);}public static boolean check(int kth) {// 利用二分圖最大匹配來求解，小于等于kth（第K大值）的元素個數（即二分圖最大匹配）int smallerCount = 0;// 記錄每個列號的匹配成功的行號int[] match = new int[m];// 初始時每個列號都處于未配對狀態，此時將列號配對的行號賦值為-1Arrays.fill(match, -1);// 遍歷行號，每個行號對互相心儀的列號發起配對請求for (int i = 0; i < n; i++) {// 記錄增廣路訪問過的列號boolean[] vis = new boolean[m];if (dfs(i, kth, match, vis)) smallerCount++;}return smallerCount >= n - k + 1;}public static boolean dfs(int i, int kth, int[] match, boolean[] vis) {// 行號 i 發起了配對請求// 遍歷每一個列號jfor (int j = 0; j < m; j++) {// 如果當前列號j未被增廣路探索過 && 當前列j行i可以配對（如果行列號位置(i,j)對應矩陣元素值小于等于kth（第K大值），則可以配對）if (!vis[j] && matrix[i][j] <= kth) {vis[j] = true;// 如果對應列號j未配對，或者，已配對但是配對的行號match[j]可以找到其他列號重新配對if (match[j] == -1 || dfs(match[j], kth, match, vis)) {// 則當前行號i 和 列號j 可以配對match[j] = i;return true;}}}return false;}
}

本案例參考&鳴謝：

華為OD機試 - 矩陣匹配（Java & JS & Python & C & C++）_od 矩陣匹配-CSDN博客

8、分配方案的最大效益問題

通用思路：

1）PriorityQueue：堆的使用。

2）動態規劃：不關心具體方案，只關心最值情況優先考慮動態規劃的可能。

#案例1-貪心歌手

一個歌手準備從A城去B城參加演出

按照合同，他必須在T天內趕到
歌手不能往回走
每兩座城市之間需要的天數都可以提前獲知。
歌手在每座城市都可以在路邊賣唱賺錢。經過調研，歌手提前獲知了每座城市賣唱的收入預期: 如果在一座城市第一天賣唱可以賺M，后續每天的收入會減少D(第二天賺的錢是M - D，第三天是M-2D…)如果收入減到0就不會再少了。
歌手到達后的第二天才能開始賣唱。如果今天賣過唱，第二天才能出發

貪心的歌手最多可以賺多少錢?

輸入描述

第一行兩個數字 T 和 N，中間用空格隔開 T 代表總天數; N 代表路上經過N座城市; 0 < T < 1000 ,0 < N < 100

第二行N+1個數字，中間用空格隔開代表每兩座城市之間耗費的時間。其總和<=T。

接下來N行，每行兩個數字M和D，中間用空格隔開.

代表每個城市的收入預期。

0< M <1000, 0 < D < 100

輸出描述

一個數字。代表歌手最多可以賺多少錢。以回車結束

示例1

輸入：
10 2
1 1 2
120 20
90 10輸出：
540說明：
總共10天，路上經過2座城市。 路上共花1+1+2=4天 剩余6天最好的計劃是
在第一座城市待3天，在第二座城市待3天 在第一座城市賺的錢:120+100+80=300 
在第二座城市賺的錢:90+80+70=240 
一共300+240 = 540

代碼：

思路：

1）每次都待預期收入最高的城市，待完更新該城市的最新預期。

2）數據結構堆的使用，每次放入數據都會按比較器定義的大小順序進行放入。

package algorithm.huawei;import java.util.ArrayList;
import java.util.List;
import java.util.PriorityQueue;
import java.util.Scanner;public class Test82 {public static void main(String[] args) {Scanner in = new Scanner(System.in);while (in.hasNextInt()) {int t = in.nextInt();//t天int n = in.nextInt();//n個城市in.nextLine();int route = 0;//路上耗時for(int i=0;i<n+1;i++){route+=in.nextInt();}in.nextLine();City[] citys = new City[n];PriorityQueue<City> pq = new PriorityQueue<City>((c1,c2)->c2.fee-c1.fee);for(int i=0;i<n;i++){int fee=in.nextInt();int q=in.nextInt();City city = new City(fee,q);pq.add(city);in.nextLine();}
//			Arrays.sort(citys,(c1,c2)->c2.fee-c1.fee);int max=0;int i=0;int k=0;//當前城市待的天數int lest = t-route;//剩余天數while(lest>0){lest--;City city = pq.poll();int fee=city.fee;int q=city.q;max+=fee;city.fee=fee-q;pq.add(city);}System.out.println(max);}}}class City{int fee;int q;public City(int fee, int q) {super();this.fee = fee;this.q = q;}}