論文閱讀 - Intriguing properties of neural networks

Intriguing properties of neural networks

經典論文、對抗樣本領域的開山之作

發布時間：2014

論文鏈接: https://arxiv.org/pdf/1312.6199.pdf

作者：Christian Szegedy, Wojciech Zaremba, Ilya Sutskever, Joan Bruna, Dumitru Erhan, Ian Goodfellow, Rob Fergus

寫在前面：該文章已經發表10年了，該領域的發展十分迅速，本文中的一些觀點可能并不準確

核心觀點

深度神經網絡是高度表達性 (highly expressive models) 的模型。由于其復雜和多層次的結構，深度神經網絡能夠捕捉到數據中極其微妙和復雜的模式。然而，這種復雜性同時也意味著網絡內部的決策過程很難被人類理解，對人們來說有些違反直覺 (counter-intuitive)。

在這篇論文中，作者介紹了兩個十分有趣的屬性：

通過不同的單元分析方法，高層單元本身 (individual high level units) 與它們的隨機線性組合 (random linear combinations of high level units) 在功能上看起來并無差別。這表明在神經網絡的高層中，包含語義信息的是空間，而不是單個單元。
深度神經網絡學習的輸入輸出映射在很大程度上是相當不連續的。通過施加幾乎察覺不到的擾動，就可以使網絡錯誤地分類一個圖像，這種擾動是通過最大化網絡的預測誤差找到的。此外，這些擾動的具體性質不是學習的隨機產物：相同的擾動可以導致另一個網絡（該網絡在數據集的不同子集上訓練）錯誤分類相同的輸入。

對觀點1的解釋

高層單元與隨機線性組合之間無區別："高層單元"指網絡中較靠近輸出層的那些單元。這意味著，如果取一些高層的單元，不論是單獨考慮還是將它們通過某種線性方式組合起來，從分析這些單元的角度來看，無法區分出它們之間的差別。這個觀察挑戰了我們通常認為的“特定單元負責特定高級特征”的理解。
語義信息的空間：由于單個單元和它們的組合在功能上沒有區別，這表明高層次的語義信息并不是儲存在單個神經元中，而是分布在整個空間中。這里的“空間”指的是由這些高層單元構成的多維空間，意味著信息是以某種分布的形式存在的，而不是局限于某個單個單元。
對深度學習的理解：神經網絡處理信息和提取特征的方式可能比我們之前理解的要復雜得多。而不是單個單元對應單一的、明確的特征，更多的是整個單元集合以一種分布的方式共同表達了高級的語義信息。

在深度神經網絡的高層中，重要的不是單個的單元，而是單元們形成的整體空間。這個空間以一種我們還不完全理解的方式，包含了輸入數據的抽象和高級的語義信息。

對觀點2的解釋

輸入輸出映射的不連續性：深度神經網絡將輸入數據（如圖像）映射到輸出（如分類標簽）的過程并不是平滑連續的。這意味著，即使是非常微小的改變也可能導致輸出結果的巨大變化。例如，一個圖像被正確分類為“貓”，但當這個圖像被稍微修改后，即使這種修改幾乎肉眼不可見，網絡可能會錯誤地將其分類為“狗”。
擾動的發現和影響：這些細微的擾動是通過優化 (optimization) 找到的，目的是最大化網絡的預測誤差。這表明可以系統地生成這樣的擾動，也表明深度神經網絡在其決策邊界周圍可能存在著“盲區”，即那些對擾動高度敏感的區域。
擾動的非隨機性和普遍性：這些導致誤分類的擾動并不是隨機產生的，也不是特定于某個網絡的。相同的或類似的擾動可以導致在不同數據集上訓練的其他網絡也產生錯誤的分類結果。這意味著這種脆弱性是深度學習模型普遍存在的問題，而不僅僅是個別模型的特定缺陷。

在安全性方面，攻擊者可能利用這一點生成擾動，以誤導模型做出錯誤的決策；在魯棒性方面，推動了對神經網絡魯棒性研究，即如何設計出能夠抵抗這類細微擾動影響的模型。

背景知識

泛化

局部泛化 (local generalization):
- 模型在訓練數據點附近的輸入空間進行有效預測的能力
- 基于假設：輸入空間中相互靠近的點（在某個小的鄰域內）應當具有相似的輸出
- 局部泛化反映了模型對于輕微擾動（如噪聲）的魯棒性，即這些小變動不會導致模型預測結果的顯著改變
非局部泛化 (non-local generalization):
- 模型在輸入空間中遠離訓練數據點的區域做出準確預測的能力
- 這涉及到對輸入空間的更廣泛區域的泛化，包括那些與訓練樣本在特征空間中相差較遠的點
- 非局部泛化需要模型在沒有直接數據支持的情況下推斷輸出，這通常依賴于模型對數據的高層次抽象和理解。例如，一個模型可能已經學習到“貓”的高級特征，如形狀和紋理，因此即使是在訓練數據中從未出現過的貓的新圖片，模型也能正確分類。

總的來說，局部泛化關注點是模型對訓練數據的微小變化的響應，而非局部泛化關注的是模型對于新的、可能在訓練數據中沒有直接例子的情況的處理能力。

特征提取 (feature extraction)

在傳統的計算機視覺系統中，顏色直方圖 (histogram of colors) 和量化的局部導數 (quantized local derivatives) 是常見的特征.

顏色直方圖：顏色直方圖是圖像中顏色分布的圖形表示。它統計了每種顏色在圖像中出現的頻率。由于顏色是視覺信息的直觀屬性，所以顏色直方圖提供了一種簡單的方式來描述和分析圖像的顏色組成。這使得比較不同圖像的顏色分布變得直觀，且不依賴于圖像的大小或者顏色在圖像中的具體位置。
量化的局部導數：局部導數，如圖像的邊緣，是通過檢測像素強度的變化來識別的。量化意味著這些導數值被簡化為有限的幾個級別。這些局部導數可以表示圖像中物體的邊界和紋理信息，是圖像分析的基本工具。

這些特征容易理解，因為它們是從人類的視覺經驗中抽象出來的基礎視覺屬性。顏色和邊緣是人類用來理解世界的基本視覺線索，所以這些特征可以與我們對圖像內容的直觀理解直接相連。在機器學習模型中使用這些特征可以幫助系統在一定程度上模仿人類的視覺識別過程。

Kernel methods

Kernel methods 是一類算法，在機器學習和統計學中被廣泛用于模式識別、分類和回歸問題。這些方法的核心思想是通過一個函數（即“核函數”）將輸入數據映射到一個高維特征空間，在這個高維空間中，數據點可能更容易被線性分割或分類。Kernel方法的一個關鍵特性是，它們能夠處理非線性關系而無需顯式地定義高維映射，這是通過核技巧（kernel trick）實現的。

Kernel技巧利用核函數來計算輸入數據點之間的相似度，核函數對應于高維特征空間中的內積。這允許算法在原始輸入空間中間接計算出高維特征空間中的關系，而不需要進行實際的映射，從而避免了直接在高維空間中計算的高昂計算成本。

最著名的kernel方法之一是支持向量機（SVM），它使用核函數來找到最佳的決策邊界，或者說超平面，該超平面可以將數據分割成不同的類別。

當文中提到“對于深度神經網絡，許多核方法所依賴的平滑性假設不成立”時，它可能是在指出與傳統的核方法（這些方法假設通過合適的核函數可以在高維空間實現平滑的決策邊界）相比，深度神經網絡在學習數據表示時表現出不同的特性。這暗示了深度網絡可能能夠學習出更復雜的模式或決策邊界，這些模式或邊界在核方法的傳統框架下可能無法捕捉。

盒約束優化問題 (box-constrained optimization problem)

在解決盒約束優化問題時，通常會使用一些特定的算法，如梯度投影法（projected gradient method）、有界限制的BFGS（L-BFGS-B）等，這些算法能夠在搜索最優解的同時保持所有變量在約束的范圍內。

框架與數據集

本論文在幾個不同的網絡和三個數據集上進行了大量的實驗：

MNIST dataset
- “FC”(Fully Connected)：由一個或多個隱藏層和一個Softmax分類器組成的簡單全連接網絡
- “AE”(Autoencoder)：在自動編碼器上訓練的分類器
ImageNet dataset
- AlexNet網絡：具體可參見論文：“Imagenet classification with deep convolutional neural networks”
來自 Youtube 的10M圖像樣本
- “QuocNet”：具有10億可學習參數的無監督訓練網絡

對于MNIST實驗，我們使用了帶有權重衰減 $λ$ 的正則化。此外，在一些實驗中，我們將MNIST訓練數據集分成兩個互不相交的數據集 $P_1$ 和 $P_2$ ，每個數據集包含30000個訓練樣本。

Units of: $φ (x)$

傳統計算機視覺通常依賴于特征提取 (feature extraction)，通常來說，一個簡單的特征很容易理解，就比如：顏色直方圖和量化的局部導數，這也使得人們可以將特征空間中的各個坐標與輸入域中的有意義的變化聯系起來。

在深度神經網絡中，類似的推理也被應用于嘗試解釋計算機視覺問題。在這些工作中，研究者們將隱藏單元的激活解釋為有意義的特征，并尋找能夠最大化這個單個隱藏單元激活值的輸入圖像。簡單地說，他們試圖找到哪些輸入圖像會引發神經網絡中某個特定單元的最強激活反應，這樣的激活被認為是捕捉到了某個重要特征，可以表示如下：
$x'=\underset{x \in \mathcal{I}}{\text{arg max}} \langle \phi(x), e_i \rangle$
$x^{'}$ 表示滿足（或接近）最大可達值(attainable value)的圖像視覺檢查

$e_i$ 表示第 $i$ 個隱藏單元相關聯的自然基向量

$\mathcal{I}$ 表示保留集，是從數據分布中選取的，但網絡沒有在其上訓練的圖像集合

$\text{arg max}_x f(x)$ 表示函數 $f (x)$ 取最大值時對應的自變量 $x$ 的值，在這個具體公式中表示，尋找集合 $\mathcal{I}$ 中的一個元素 $x$ ，使得內積 $\langle \phi(x), e_i \rangle$ 最大。換句話說，它找的是哪一個 $x$ 與向量 $e_i$ 有最大的“匹配度”或“相關性”。在深度學習的應用中，這通常意味著找到使某個特定神經網絡層的激活最大化的輸入 $x$ 。

3. 神經網絡中的盲點（尋找對抗樣本）

單位級別的檢查 (unit-level inspection) 幾乎沒什么作用，而全局的、網絡級別的檢查方法在解釋模型做出分類決策上可能會是有用的。就比如，用于識別輸入中能使得給定輸入實例進行正確分類的那部分（換言之，可以使用經過訓練的模型進行弱監督定位），這種全局分析使我們更好地理解訓練后的網絡所代表的從輸入到輸出的映射。

通常來說，神經網絡的輸出層單元是其輸入的一個高度非線性函數。當它使用交叉熵損失訓練時（使用Softmax激活函數），它代表了給定輸入（以及到目前為止呈現的訓練集）標簽的條件分布。有人認為，輸入與神經網絡輸出單元之間的深層非線性層堆疊是模型編碼輸入空間上的非局部泛化先驗的一種方式。換句話說，輸出單元能夠給輸入空間中那些沒有訓練示例在其附近的區域分配極小的概率。例如，從不同視角看相同對象，雖然這些視角在像素空間中距離相對較遠，但它們既共享標簽也共享原始輸入的統計結構。

具體解釋如下：

損失函數衡量的是模型預測的概率分布與真實標簽的概率分布之間的差異。在理想情況下，模型預測的概率分布應該與真實的分布完全一致，這時交叉熵損失會是最低的。所以，可以說對于分類問題，使用交叉熵損失，相當于用神經網絡來計算輸入圖像對應類別的條件分布。
非局部泛化先驗 (non-local generalization prior) 的概念指的是神經網絡能夠對那些在訓練數據中沒有直接出現過的輸入進行有效泛化的能力。這意味著，即使某個輸入（或輸入的某個區域）在訓練集中沒有直接的對應樣本，網絡仍然能夠基于它對整個輸入空間的學習，對這個新的、未見過的輸入做出合理的預測。輸入與神經網絡輸出單元之間的深層非線性層堆疊也有人理解為神經網絡在對輸入空間的非局部泛化先驗進行編碼。
輸出單元能夠給輸入空間中那些沒有訓練示例在其附近的區域分配極小但并非為0的概率 non-significant (and, presumably, non-epsilon) probabilities. 盡管這些輸入數據在特征上可能與某些類別有關聯，但根據模型通過訓練學到的信息，它認為這些數據屬于那個類別的可能性不高。這是模型嘗試對看到的和未看到的數據進行泛化和推理的一種表現，即使面對它在訓練數據中沒有直接遇到的新情況，也能做出合理的預測。
深度學習模型尤其是卷積神經網絡在圖像識別和分類中具有泛化能力。模型通過訓練，能夠識別與訓練樣本在像素層面大相徑庭的輸入，例如，能處理同一對象從未在訓練集中出現過的不同視角的圖像。這歸功于模型學習到的對象的一般性特征和統計結構，如形狀、紋理和顏色分布，而不僅僅是依賴特定的像素排列。即使是從新的、未見過的視角觀察到的對象，這些從不同角度拍攝的圖像雖然在像素級別上看似不同，但因為它們代表同一對象，所以共享相同的分類標簽和統計結構，使得網絡能夠將它們正確分類。這也展示了深度學習模型對輸入數據的深層次理解能力，它能夠識別和歸納超越像素相似性的圖像背后的抽象特征和模式。

上述論證中隱含著這樣一個論點：在非常接近訓練示例的情況下，局部泛化按照預期那樣正常工作。在這種假設下，如果給定一個很小的半徑 $\varepsilon>0$ 和輸入樣本 $x$ ，對于滿足 $r + x$ ， $||r||<\varepsilon$ ( $r$ ? 表示微小變化) 的輸入樣本依然有機會被正確的分類。這種平滑先驗通常對計算機視覺問題是有效的，即給圖像細微擾動通常不會改變它本來的類別。但是對于深層神經網絡，這篇文章的得到的結果是上述的平滑假設并不成立。并且可以通過簡單的優化過程找到對抗樣本(對正確分類的輸入圖像進行不明顯的微小擾動)，讓神經網絡不能再正確分類。

當提到局部泛化工作“如預期”的時候，它指的是在模型訓練的數據點的非常近的范圍內，模型能夠保持其預測的連貫性和準確性。而非局部泛化則是挑戰模型在遠離訓練數據點的范圍內仍能保持有效預測能力的問題。

對于深度神經網絡而言，我們發現許多核方法 (kernel methods) 所依賴的平滑性假設并不成立。具體來說，我們展示了通過使用一個簡單的優化過程，我們能夠找到對抗樣本，這些是通過對正確分類的輸入圖像進行微小的、幾乎察覺不到的擾動得到的，從而使得它不再被正確分類。

從某種意義上講，我們描述的是一種通過優化以高效方式遍歷神經網絡所代表的流形 (traverse the manifold)，并在輸入空間中找到對抗樣本 (adversarial examples) 的方法。

“traverse the manifold”（遍歷流形）是指在神經網絡所代表的數據空間（或稱為“流形”）內進行搜索或探索的過程。這里的“流形”是數學上的一個概念，用來描述在局部呈現出歐幾里得空間特性的空間。在深度學習中，神經網絡可以被看作是在高維數據空間中定義了一個復雜的流形，該流形通過網絡的層次結構將輸入數據映射到輸出結果。因此，“遍歷流形”具體指的是通過優化方法在這個高維空間內移動，以尋找那些能夠改變網絡輸出的特定輸入值，即尋找到能夠使神經網絡輸出錯誤結果的對抗樣本

對抗樣本代表了流形中這個高維空間的特定區域，這些區域的存在可能會導致模型的預測錯誤，但這些區域出現的概率很低，使得通過隨機采樣來發現這些區域變得非常困難。已經有許多計算機視覺模型在訓練過程中采用輸入變形（比如旋轉、縮放、剪切圖像），以提高模型的魯棒性和收斂速度。這些變形從統計上來看對于給定示例是低效的：它們高度相關，并且在整個模型訓練過程中都來自同一個分布。

然而，盡管這些輸入變形能增加數據的多樣性，但從統計學的角度來看，它們是低效的。原因是這些變形高度相關，而且整個訓練過程中，這些變形產生的數據都來自于同一個分布。這意味著，盡管數據通過變形在表面上看起來不同，但從根本上講，它們帶給模型學習的信息是有限的，因為這些變化是可預測的，且在整個訓練過程中沒有本質的變化。如果在訓練過程中一直重復使用相同的變形方法，模型可能會過于適應這些特定的變形而不是學會從根本上理解圖像的內容。

我們提出了一種方案，利用模型及其在訓練數據周圍局部空間建模方面的不足，使這一過程自適應。這種方法能夠識別出模型在理解訓練數據特別是數據的局部細節方面存在的問題或不足。利用這種識別出來的信息，該方法能夠自動調整訓練過程，使其更加針對性地解決這些問題，從而提高模型的性能。

我們的方案與硬負采樣（hard-negative mining）有密切的聯系，因為它們在想法上是接近的：在計算機視覺中，“硬負例”指的是那些模型錯判為負例（即非目標類）的正例樣本，或者說，它們是模型預測錯誤的案例，但按理應該被正確分類的。這些樣本對于模型來說是“難題”，因為模型很難準確地將它們分類到正確的類別中。即，被模型錯誤地判斷為低概率（即模型認為它們屬于某一類的可能性很低）的示例，但實際上，這些示例應該被判斷為高概率（即應該很容易被識別為某一類）。通過識別這些模型當前處理不好的示例，并在訓練集中對它們給予更多的重視（例如，通過增加它們的權重或更頻繁地將它們納入訓練批次中），可以促使模型更加關注于改進其在這些特定情況下的表現。正如所述的那樣，本工作提出的優化問題也以一種類似于硬負采樣的方式被使用。

4.1 正式描述

$f:\mathbb{R}^m \rightarrow \{1, \ldots, k\}$ 為分類器，接收一個 $m$ 維的圖像像素值向量作為輸入，將其映射到一個離散的標簽集 ${1 ... k}$ 中， $k$ ? 為類別數。

給定圖片 $\in \mathbb{R}^m$ 以及目標標簽 $\in \{1, \ldots, k\}$ ，我們想解決如下的盒約束優化問題 (box-constrained optimization problem)：

$\text{Minimize $||r||_2$ subject to:} \\ 1.f(x+r) = l \\ 2.x+r \in [0,1]^m$

存在約束：

找到一個擾動向量 $r$ ，使得擾動后的圖像 $x + r$ 被分類器 $f$ 識別為目標標簽 $l$
$\in [0,1]^m$ ：擾動后的圖像像素值在合理范圍

$D (x, l)$ 用來尋找距離原始圖像 $x$ 最近的、被分類器 $f$ 錯誤分類的圖像。最小值 $r$ 可能并不唯一，我們用 $x + r$ 表示通過 $D (x, l)$ 任意選擇的一個最小值。很明顯， $D (x, f (x)) = f (x)$ ，因此當 $f (x) \neq = l$ 時，這個任務才是有意義的?。

通常，$ D(x,l) $ 的精確計算是一個困難問題，因此我們使用盒約束L-BFGS (box-constrained L-BFGS) 對其進行近似。我們通過進行線性搜索來找到最小值 $c > 0$ ，對于該最小值，以下問題的極小值 $r$ 滿足 $f (x + r) = l$
$\text{Minimize } c|r| + \text{loss}_f(x + r, l) \quad \text{subject to } x + r \in [0, 1]^m$
在凸損失 (convex losses) 的情況下，這種懲罰函數方法 (penalty function method) 將給出精確解，但是神經網絡通常是非凸的，因此在這種情況下我們會得到一個近似值。

實驗結果

我們的最小失真 (minimum distortion) 函數 $D$ 具有以下有趣特性，我們將在本節中通過非正式證據和定量實驗加以說明:

在上述提及的神經網絡中，對于每個樣本，我們總是設法生成非常接近的，視覺上難以區分的，并且被原始網絡錯誤分類的對抗樣本，如下圖所示（注：2024.4 鏈接已失效）

跨模型泛化能力：在 A 模型上產生的對抗樣本，有很大一部分在 B 模型（和 A 模型結構相同，超參數不同）上也有效
跨數據集泛化能力：在 D1數據集訓練得到的模型上產生的對抗樣本，在 D2 數據集訓練得到的模型上也有效，D1 和D2 屬于不同的子集

上述結果表明，對抗樣本在某種程度上是普遍的，而不僅僅是過度擬合特定模型或特定選擇訓練集的結果。并且，將對抗樣本用于訓練可能會提高結果模型的通用性。我們的初步實驗也為MNIST提供了積極的證據來支持這一假設：我們通過保留一組對抗樣本作為隨機子集，成功地訓練了測試誤差低于1.2％的兩層100-100-10非卷積神經網絡，通過維護了一個動態對抗樣本池，在每次訓練迭代中，一部分對抗樣本會被新生成的對抗樣本替換。

我們使用了權重衰減 (weight decay)，但沒有使用 (dropout)。作為比較，僅通過權重衰減進行正則化，該規格的識別誤差為1.6％，但通過使用精心設計的 Dropout 可將其降低至1.3％左右。一個很關鍵的細節是在訓練過程中，針對每一層的輸出生成對抗樣本并用這些樣本來訓練該層以上的所有層。該網絡以交替的方式進行訓練，除了原始訓練集之外，還分別維護和更新每一層的對抗樣本庫。根據觀察，高層的對抗樣本似乎比輸入層或較低層的對抗樣本有用得多。在未來的工作中，我們計劃系統地比較這些影響。

出于空間考慮，我們只介紹我們執行的MNIST實驗的代表性子集（參見下表）的結果。此處顯示的結果與各種非卷積模型的結果一致。對于MNIST，我們尚無卷積模型的結果，但我們與 AlexNet 進行的首次定性實驗讓我們有理由相信卷積網絡的行為也可能相似。我們的每個模型都經過L-BFGS訓練直至收斂。前三個模型是具有不同權重衰減參數 $λ$ 的線性分類器，將二次權重衰減 $loss_{decay}=\lambda \sum w_i^2/k$ （ $k$ ? 是一層中單元的數量）填加至總損失中。

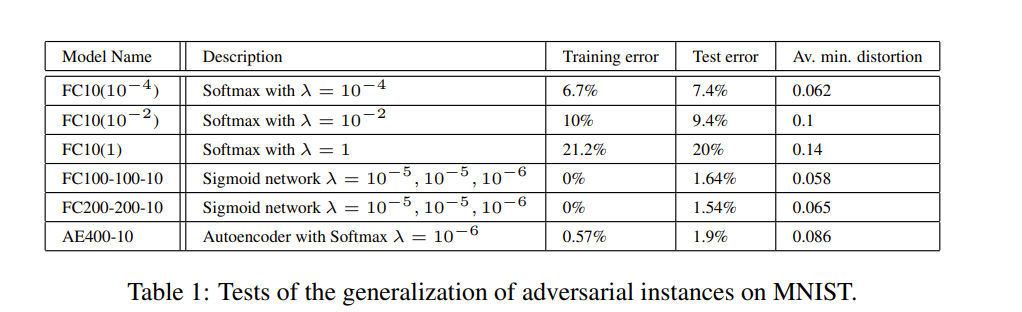
具體來看該表格，左側是具體的模型，前三個是沒有隱藏層的簡單 softmax 分類器 FC10( $λ$ ) , 其中 FC10(1) 表示以 $λ = 1$ 這種極端情況進行訓練，來測試是否仍然可以產生對抗樣本。另外兩個模型是具有兩個隱藏層和一個分類器的簡單 sigmoidal 神經網絡。最后一個模型AE400-10 是由具有Sigmoid型激活的單層稀疏自動編碼器 (sparse autoencoder) 和帶有 Softmax 分類器的400個節點組成的。該網絡已經過訓練獲得了非常高質量的第一層過濾器并且沒有對該層進行微調。

最后一列測量在訓練集上達到 0％精度所需的最小平均像素級別失真 (the minimum average pixel level distortion)，也就是100%分類失敗，這個失真是通過 $\sqrt{\frac{\sum(x_i'-x_i)^2}{n}}$ 來衡量的，其中 n 是圖像像素的數目，像素值縮放到 $[0 ， 1]$ 范圍內。

跨模型的泛化能力

在我們的第一個實驗中，我們為給定的網絡生成了一組的對抗樣本，并為每個其他網絡提供這些實例來測量誤分類實例的比例。結果如下，最后兩行用給定量的高斯噪聲所引起的失真誤差作為參考。除了一個模型以外的所有模型，即使標準差為0.1的噪聲也大于我們對抗性噪聲的標準差。圖7展示了該實驗中使用的兩個網絡生成的對抗樣本的可視化。總的來說，即使對于使用不同超參數訓練的模型，對抗樣本也有所影響。盡管基于自動編碼器的版本似乎可以對抗敵手，但也不能完全避免。

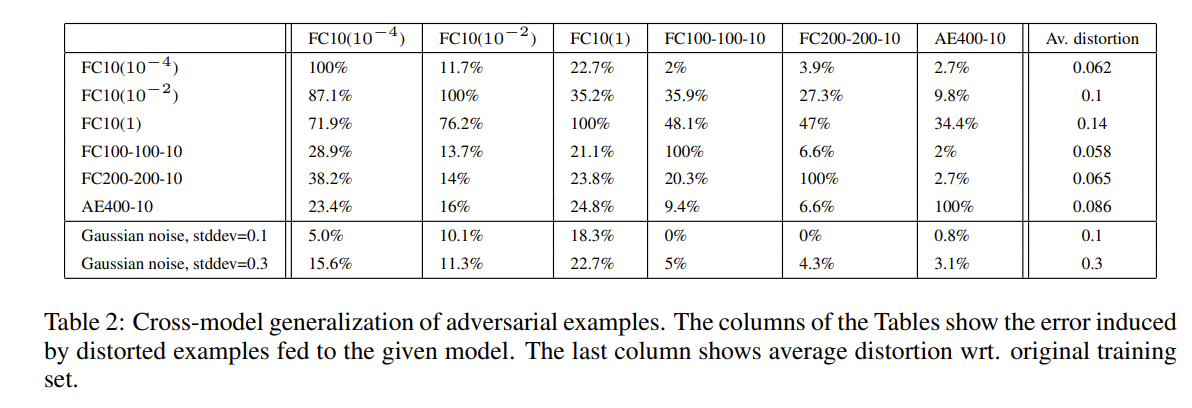
接下來研究有關數據集的問題，生成對抗樣本的難度是否僅取決于訓練集的特定選擇嗎，而且以上部分的使用都是在相同的數據集進行訓練的，那么對抗樣本的效果可以推廣到在完全不同的訓練集上訓練的模型嗎？

跨數據集泛化能力

為了研究交叉訓練集的泛化，我們將60000個MNIST訓練圖像劃分為30000個每組的 $P_1$ 和 $P_2$ 兩個部分，并訓練了三個具有 Sigmod 激活函數的非卷積網絡：在 $P_1$ 上訓練 FC100-100-10 和 FC123-456-10，在 $P_2$ 上訓練 FC100-100-10。在 $P_1$ 上訓練兩個網絡的原因是要研究同時更改超參數和訓練集的累積效應。FC100-100-10 和 FC100-100-10’ 共享相同的超參數：它們都是100-100-10網絡，而FC123-456-10 具有不同數量的隱藏單元。表3總結了有關這些模型的基本參數。

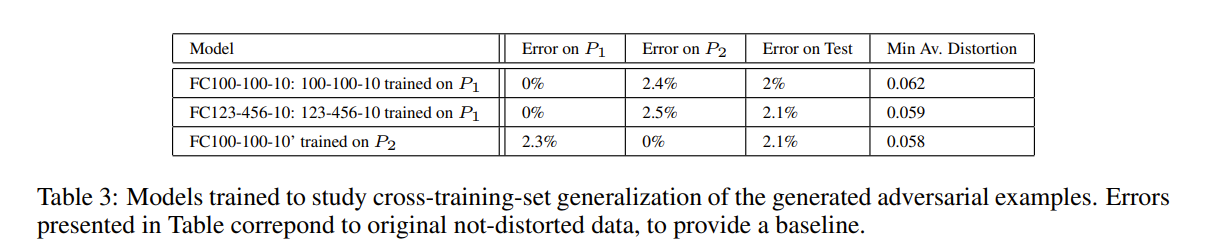
在為測試集生成具有100％錯誤率且失真最小的對抗樣本之后，我們將這些示例提供給每個模型。

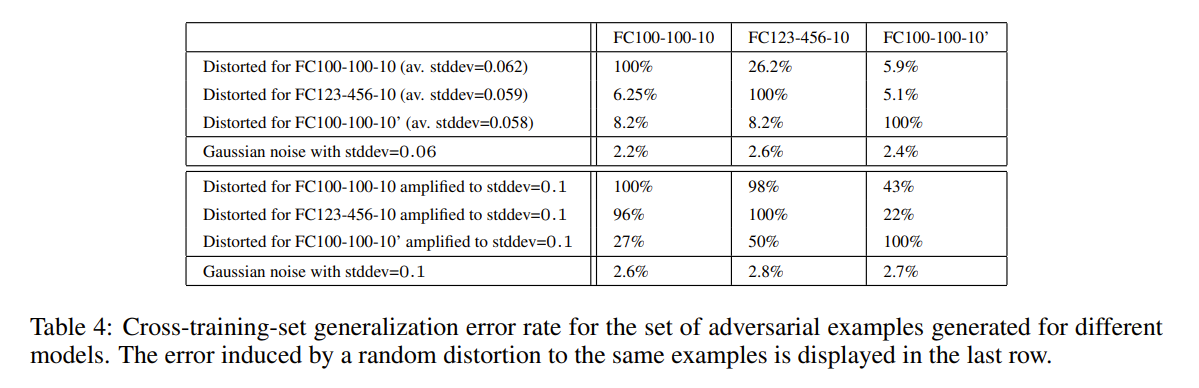
在最后的實驗中，我們衡量失真的效應為 $x+0.1\frac{x'-x}{||x'-x||_2}$ 而不是 $x^{'}$ 。這將失真平均提高了40％，stddev 從0.06擴大到 0.1。我們可以得出結論：即使在不相交的訓練集上訓練的模型，對抗樣本依舊也所影響，盡管其有效性大大降低。

神經網絡穩定性的頻譜分析

本部分涉及許多數學公式證明，一個專門講解這部分的證明過程的視頻鏈接如下：https://www.youtube.com/watch?v=df_NZyGeVXg

討論

文章證明了深度神經網絡在個體單元的語義含義以及在不連續性方面都表現出了一些違反直覺的屬性。對抗負例 (adversarial negatives) 的存在似乎與網絡達到高泛化性能的能力相矛盾。也確實是這樣，雖然這些樣例確實不太容易與常規樣例區分，但如果神經網絡真的泛化很好，怎么會被這些對抗樣本所混淆呢？一個可能的解釋是，對抗負例集的出現具有極低的概率，因此在測試集中從未（或很少）被觀察到，但它卻是稠密的（類似于有理數的分布），因此幾乎在每一個測試案例的附近都能找到對抗負例。然而，我們對其出現的頻率還缺乏深入理解，因此這個問題應該在未來的研究中得到關注。