0. 前言

圖生成算法是指用于創建模擬圖或網絡結構的算法，這些算法可以根據特定的規則和概率分布生成具有特定屬性的圖，用于模擬各種復雜系統，如社交網絡、生物網絡、交通網絡等。傳統圖生成技術已有數十年歷史，并可用作各種應用的基準，但這些技術在生成的圖類型上存在限制。這些方法大多數都專注于輸出特定的拓撲結構，因此不能簡單地模仿給定網絡。在本節中，我們將介紹兩種經典圖生成技術：Erd?s–Rényi 模型和小世界 (small-world) 模型。

1. 圖生成技術

圖生成是生成新圖的技術，并且希望所生成的圖具有真實世界中圖的性質。作為一個研究領域，它為了解圖如何工作和演化提供了新思路。它還可以直接應用于數據增強、異常檢測、藥物發現等領域。我們可以將圖生成分為兩種類型：一種是模仿給定圖生成具有類似性質的逼真圖數據 (例如，數據增強)，另一種是目標導向圖生成，即創建優化特定指標的圖(例如，分子生成)。

2. Erd?s–Rényi模型

Erd?s–Rényi 模型是最簡單、最流行的隨機圖 (random graph model) 模型，由匈牙利數學家 Paul Erd?s 和 Alfréd Rényi 于 1959 年提出，該模型有兩個變體： $G(n,p)$ 和 $G(n,M)$。
在 $G(n,p)$ 模型中：給定節點數量和節點連接的概率，嘗試隨機地將每個節點與其他節點連接起來，以創建最終的圖。這意味著存在 $C_2^n$ 種可能的連接。另一種理解概率 $p$ 的方式是將其視為改變網絡密度的參數。使用 networkx 庫可以直接實現 $G(n,p)$ 模型。

(1) 導入 networkx 庫：

import networkx as nx
import matplotlib.pyplot as plt

(2) 使用 nx.erdos_renyi_graph() 函數生成一個有 10 個節點 (n = 10)、邊創建概率為 0.5 (p = 0.5) 的圖 $G$：

G = nx.erdos_renyi_graph(10, 0.5)

(3) 使用 nx.circular_layout() 函數為生成的節點布局 pos，也可以使用其他布局，但這種布局便于比較不同的 p 值：

pos = nx.circular_layout(G) 

(4) 使用 nx.draw() 以 pos 布局繪制圖 $G$：

nx.draw(G, pos=pos)
plt.show()

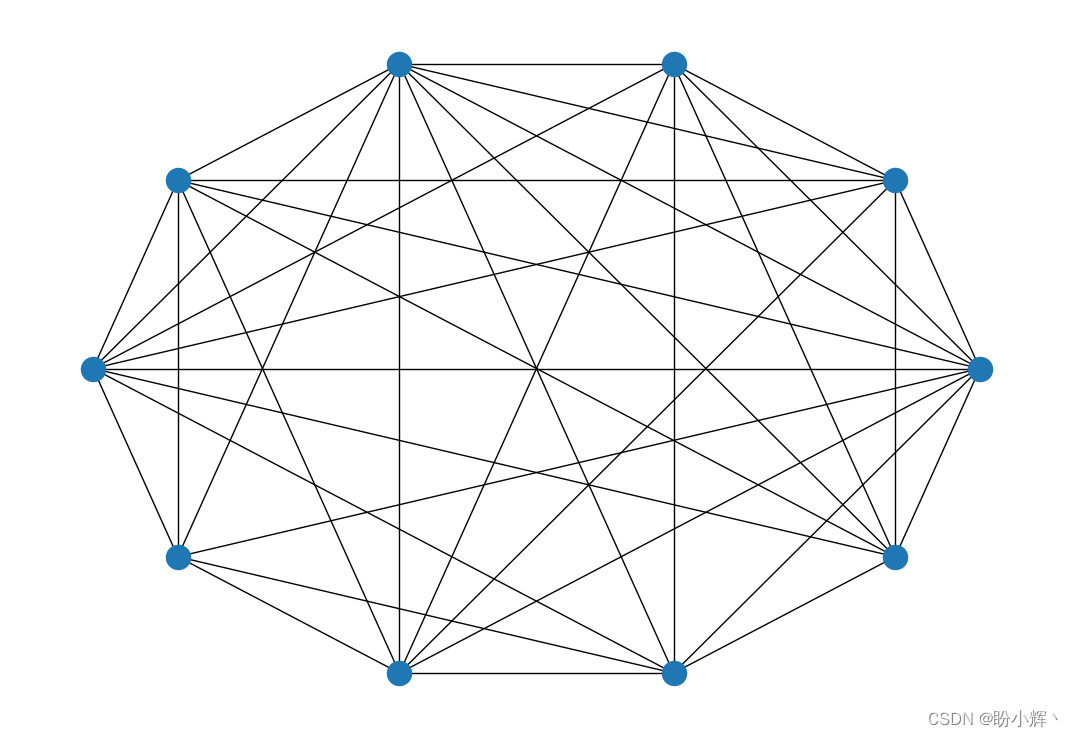
以 0.1 和 0.9 的概率重復以上過程：

G = nx.erdos_renyi_graph(10, 0.1)
pos = nx.circular_layout(G) 
nx.draw(G, pos=pos)
plt.axis('off')
plt.show()G = nx.erdos_renyi_graph(10, 0.9)
pos = nx.circular_layout(G) 
nx.draw(G, pos=pos)
plt.axis('off')
plt.show()

可以看到，當 $p$ 值較低時，存在許多孤立節點，而當 $p$ 值較高時，圖中的節點具有高度互聯性。
在 $G(n，M)$ 模型中，從所有具有 $n$ 個節點和 $M$ 條邊的圖中隨機選擇一個圖。例如，如果 $n=3$，$M=2$，則有三個可能的圖，如下圖所示，$G(n,M)$ 模型將隨機選擇其中一個圖。這是解決同一問題的不同方法，但通常不如 $G(n,p)$ 模型流行，因為一般情況下它更難以分析：

也可以使用 nx.gnm_random_graph() 函數在 Python 中實現 $G(n,M)$ 模型：

G = nx.gnm_random_graph(3, 2)
pos = nx.circular_layout(G) 
nx.draw(G, pos=pos)
plt.axis('off')
plt.show()

$G(n,p)$ 模型假設鏈接是獨立的，即它們不會相互干擾。然而，對于現實世界中的大多數圖而言，這一假設并不成立。

3. 小世界模型

小世界 (small-world) 模型于 1998 年由 Duncan Watts 和 Steven Strogatz 提出，旨在模仿生物和社交網絡的行為。其主要思想是，現實世界的網絡并非完全隨機(如 Erd?s–Rényi 模型)，但也并非完全規則(如網格)，通常拓撲結構介于兩者之間，因此我們可以使用系數對其進行插值。小世界模型生成的圖兼具以下特點：

• 路徑短：網絡中任意兩個節點之間的平均距離相對較小，這使得信息很容易在整個網絡中快速傳播
• 聚類系數高： 網絡中的節點往往彼此緊密相連，形成密集的節點集群

許多算法都具有小世界特性。接下來，我們將介紹最初的 Watts-Strogatz 模型，可以通過以下步驟實現：

1. 初始化一個有 $n$ 個節點的圖
2. 每個節點與其 $k$ 個最近的鄰居相連(如果 $k$ 為奇數，則與 $k?1$ 個鄰居相連)
3. 節點 $i$ 和 $j$ 之間的每個鏈接在 $i$ 和 $k$ ($k$ 為另一個隨機節點)之間重新連接的概率為 $p$

在 Python 中，可以通過調用 nx.watts_strogatz_graph() 函數實現：

G = nx.watts_strogatz_graph(10, 4, 0.5)
pos = nx.circular_layout(G) 
nx.draw(G, pos=pos)
plt.axis('off')
plt.show()

與 Erd?s–Rényi 模型一樣，可以用不同的概率 $p$ 重復相同的過程：

可以看到，當 $p=0$ 時，圖是完全規則的。相反，當 $p=1$ 時，由于每個鏈接都被重新連接，所以圖完全是隨機的。通過具有中心節點和局部聚類的平衡圖來在這兩個極端之間獲得一個圖。
然而，Watts-Strogatz 模型并不能產生真實的節點度分布。它還需要固定數量的節點，這意味著它不能用于網絡的增長。

小結

本節中，介紹了經典的圖生成算法，包括 Erd?s-Rényi 模型和小世界模型。Erd?s-Rényi 模型是最早的隨機圖模型之一，它根據一定的連接概率在節點之間添加邊，從而創建一個隨機圖。小世界模型通過重連邊的方式在規則網絡上引入隨機性，從而模擬了許多真實世界網絡的“小世界”特性，即短路徑長度和高聚類系數。并使用 networkx 實現了這兩種模型以生成圖數據。

系列鏈接

圖神經網絡實戰（1）——圖神經網絡(Graph Neural Networks, GNN)基礎
圖神經網絡實戰（2）——圖論基礎
圖神經網絡實戰（3）——基于DeepWalk創建節點表示
圖神經網絡實戰（4）——基于Node2Vec改進嵌入質量
圖神經網絡實戰（5）——常用圖數據集
圖神經網絡實戰（6）——使用PyTorch構建圖神經網絡
圖神經網絡實戰（7）——圖卷積網絡(Graph Convolutional Network, GCN)詳解與實現
圖神經網絡實戰（8）——圖注意力網絡(Graph Attention Networks, GAT)
圖神經網絡實戰（9）——GraphSAGE詳解與實現
圖神經網絡實戰（10）——歸納學習
圖神經網絡實戰（11）——Weisfeiler-Leman測試
圖神經網絡實戰（12）——圖同構網絡(Graph Isomorphism Network, GIN)
圖神經網絡實戰（13）——經典鏈接預測算法
圖神經網絡實戰（14）——基于節點嵌入預測鏈接
圖神經網絡實戰（15）——SEAL鏈接預測算法