前言:本文就前期學習快速排序算法的一些疑惑點進行詳細解答,并且給出基礎快速排序算法的優化版本

一.再談快速排序

快速排序算法的核心是分治思想,分治策略分為以下三步:

1. 分解:將原問題分解為若干相似,規模較小的子問題
2. 解決:如果子問題規模較小,直接解決;否則遞歸解決子問題
3. 合并:原問題的解等于若干子問題解的合并

應用到快速排序算法:

1. 分解:快速排序算法要實現的是對整個數組進行排序,但是規模較大,要想辦法減少規模;他的解決策略是"選擇一個基準元素,將數組劃分為兩部分,左邊都是小于基準元素,右邊都是大于基準元素",不斷的重復上述過程,就能完成對整個數組的排序.對整個數組完成一次這樣的操作后,再對左右兩個區間分別執行上述過程
2. 遞歸地對兩個子數組進行快速排序，直到每個子數組的長度為0或1，此時數組已經有序。
3. 由于在遞歸過程中子數組已經被分別排序，因此不需要再進行額外的合并步驟。

二.代碼實現和細節講解

快速排序的關鍵代碼在于如何根據基準元素劃分數組區間(parttion),分解的方法有很多,這里只提供一種方法挖坑法
代碼:

class Solution {public int[] sortArray(int[] nums) {quick(nums, 0, nums.length - 1);return nums;}private void quick(int[] arr, int start, int end) {if(start >= end) return;// 遞歸結束條件int pivot = parttion(arr, start, end);// 遞歸解決子問題quick(arr, start, pivot - 1);quick(arr, pivot + 1, end);}// 挖坑法進行分解private int parttion(int[] arr, int left, int right) {int key = arr[left];while(left < right) {while(left < right && arr[right] >= key) right--;arr[left] = arr[right];while(left < right && arr[left] <= key) ++left;arr[right] = arr[left];}arr[left] = key;return left;}}

---

細節解答:
1.為什么start>=end是遞歸結束條件?

不斷的分解子問題,最終子問題的規模大小是1,即只有一個元素,此時無需繼續進行分解,start和end指針同時指向該元素

2.為什么要right先走?而不是left先走?

具體誰先走取決于基準元素的位置,在上述代碼中,基準元素(key)是最左邊的元素,如果先移動left,left先遇到一個比基準元素大的元素,此時執行arr[right] = arr[left],由于沒有保存arr[right],這個元素就會丟失
如果先走right,right先遇到一個比基準元素小的元素,此時執行arr[left]=arr[right],因為此時left并沒有移動,還是pivot,但是pivot已經被我們使用key進行保存了

3.為什么是arr[right]>=key?>不行嗎

大于等于主要是為了處理重復元素問題
例如有數組[6,6,6,6,6]如果是>,right指針不會發生移動,left指針也不會發生移動,此時陷于死循環

4.為什么叫做挖坑法

當r指針遇到第一個<pivot的元素后停止,執行arr[r] = arr[l],此時l位置就空白出來,形成了一個坑

---

三.快速排序的優化

主要有兩個優化方向:

1. 基準值pivot的選取,可以證明的是當隨機選取基準值時,快速排序的時間復雜度趨近于O(N*logN),即最好的時間復雜度
2. 重復元素的處理:如果區間內部有大量的重復元素,上述版本的快速排序算法會對相同的元素重復執行多次;為了減少冗余的操作,使用數組分三塊的思想解決,同時如果遇到特殊的測試用例(順序數組或逆序數組)時間復雜度會退化到O(N^2)

先根據一道題目(顏色分類)了解什么是數組分三塊
分析

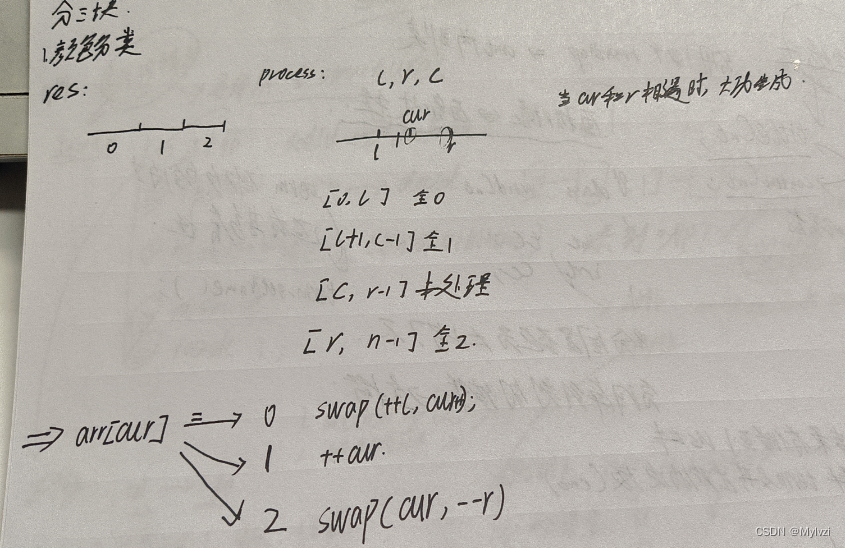
代碼:

class Solution {public void sortColors(int[] nums) {// 分治 --// 1.定義三指針int i = 0;// 遍歷整個數組int l = -1, r = nums.length;while(i < r) {if(nums[i] == 0) swap(nums,++l,i++);else if(nums[i] == 1) i++;else swap(nums,--r,i);}return;}private void swap(int[] nums,int x,int y) {int tmp = nums[x]; nums[x] = nums[y]; nums[y] = tmp;}
}

• 注意l,r的起始位置,第一個元素和最后一個元素在開始的時候屬于未處理狀態,所以`l,r不能指向這兩個元素,必須在區間之外
• 所謂的數組分三塊,就是使用三個指針去分別維護四個區間,其中的一個區間是未處理區間,隨著cur指針的不斷移動,所有的區間都被處理,最終也就只有三個區間

將上述思路應用于快速排序的parttion中,最終的結果就是劃分為三個區間

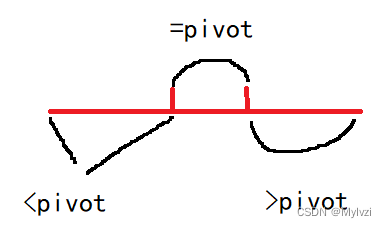
代碼實現:

class Solution {// 快速排序優化版// 分解--解決--合并public int[] sortArray(int[] nums) {qsort(nums, 0, nums.length - 1);return nums;}private void qsort(int[] nums, int start, int end) {if(start >= end) return;// 遞歸結束條件// 分解int pivot = nums[start];int l = start - 1, r = end + 1, i = start;while(i < r) {int cur = nums[i];if(cur < pivot) swap(nums, ++l, i++);else if(cur == pivot) ++i;else swap(nums, --r, i);}// [start, l]  [l+1, r-1]  [r, end]// 遞歸解決qsort(nums, start, l);qsort(nums, r, end);}private void swap(int[] nums,int i, int j) {int tmp = nums[i];  nums[i] = nums[j]; nums[j] = tmp;}
}

2.隨機選取基準值
采用隨機數的方式隨機選取基準值

        int pivot = nums[start + new Random().nextInt(end - start + 1)];//               起始位置      隨機產生的偏移量

完整的改進代碼:

class Solution {// 快速排序優化版// 分解--解決--合并public int[] sortArray(int[] nums) {qsort(nums, 0, nums.length - 1);return nums;}private void qsort(int[] nums, int start, int end) {if(start >= end) return;// 遞歸結束條件// 分解int pivot = nums[start + new Random().nextInt(end - start + 1)];int l = start - 1, r = end + 1, i = start;while(i < r) {int cur = nums[i];if(cur < pivot) swap(nums, ++l, i++);else if(cur == pivot) ++i;else swap(nums, --r, i);}// [start, l]  [l+1, r-1]  [r, end]// 遞歸解決qsort(nums, start, l);qsort(nums, r, end);}private void swap(int[] nums,int i, int j) {int tmp = nums[i]; nums[i] = nums[j]; nums[j] = tmp;}
}

• 效率明顯提升

四.快速選擇算法

快速選擇算法是基于快速排序優化版本的一種時間復雜度可達到O(N)的選擇算法,使用場景為第K大/前K大之類的選擇問題

01.數組中的第K個最大的元素
鏈接:https://leetcode.cn/problems/kth-largest-element-in-an-array/
分析

• 暴力解法就是直接使用sort進行排序,然后返回第K大即可
• 時間復雜度:O(N*logN)
• 空間復雜度:O(logN)遞歸產生的棧調用

接下來采用快速選擇算法,實現O(N)的時間復雜度
代碼:

class Solution {public int findKthLargest(int[] nums, int k) {return qsort(nums, 0, nums.length - 1, k);}private int qsort(int[] nums, int start, int end, int k) {if(start >= end) return nums[start];int pivot = nums[start + new Random().nextInt(end - start + 1)];// 數組分三塊  <pivot  ==pivot  >pivotint l = start - 1, r = end + 1, i = start;while(i < r) {if(nums[i] < pivot) swap(nums, ++l, i++);else if(nums[i] == pivot) ++i;else swap(nums, --r, i);}// [start, l]  [l+1, r - 1]  [r, end]int c = end - r + 1, b = r - 1 - (l + 1) + 1, a = l - start + 1;// 分情況討論  進行選擇if(c >= k) return qsort(nums, r, end, k);else if(b + c >= k) return pivot;else return qsort(nums, start, l, k - b - c);// 找較小區間的第(k-b-c)大}private void swap(int[] arr, int i, int j) {int tmp = arr[i]; arr[i] = arr[j]; arr[j] = tmp;}
}

• 快速選擇算法和快速排序的思想很像,不同點在于快速選擇算法只對每次parttion結果的一部分區間進行遞歸,而不是像快速排序一樣對整個區間進行遞歸,所以快速選擇算法的時間復雜度降到了O(N)