并查集
// 1.初始化
int fa[MAXN];
void init(int n)
{for (int i=1;i<=n;++i)fa[i]=i;
}// 2.查詢
找到的祖先直接返回,未進行路徑壓縮
int.find(int i){if(fa[i] == i)return i;// 遞歸出口,當到達了祖先位置,就返回祖先elsereturn find(fa[i]);// 不斷往上查找祖先
}// 3.合并
void unionn(int i,int j)int i_fa=find(i);// 找到i的祖先 int j_fa=find(j);// 找到j的祖先fa[i_fa]=j_fa;// i的祖先指向j的祖先。
}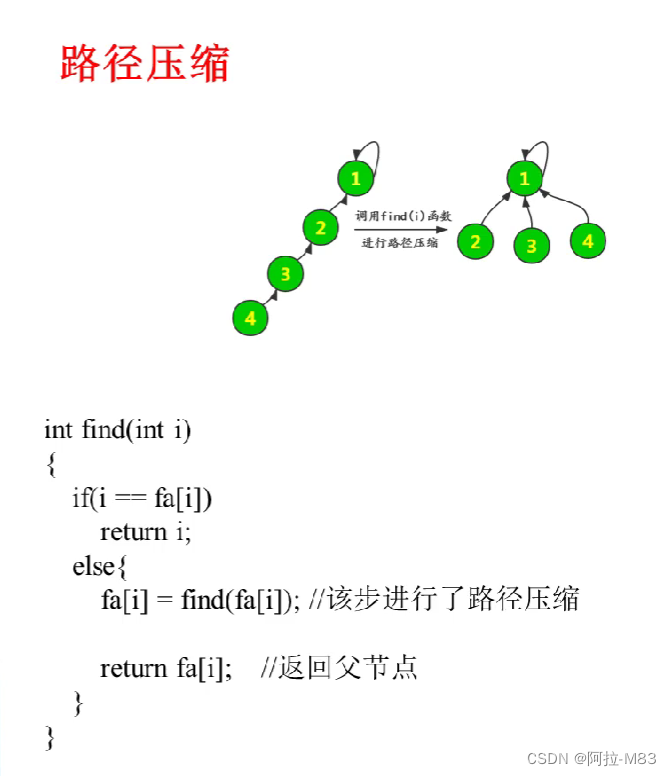
路徑壓縮,也就是在某一次find函數執行過程中,更新子節點的指向,直接指向頂級節點
107.尋找存在的路徑
題目:107. 尋找存在的路徑 (kamacoder.com)
思路:難道說,使用并查集的find函數,遍歷所有的邊,將節點的父親信息存起來,如果source和destination沒有指向同一個根節點,那么就說明不存在路徑
嘗試(不對)
import java.util.*;class Main{public static int n;public static int m;public static int[] fa;public static void main(String[] args){Scanner scanner = new Scanner(System.in);n = scanner.nextInt();m = scanner.nextInt();fa = new int[n];for(int i = 0; i<n; i++){fa[i] = i;}for(int i = 0; i<m; i++){int n1 = scanner.nextInt();int n2 = scanner.nextInt();union(n1,n2);}int source = scanner.nextInt();int destination = scanner.nextInt();if(source == find(destination)){System.out.println(1);}else{System.out.println(0);}}public static void union(int i , int j){int i_fa = find(i);int j_fa = find(j);fa[i_fa] = j_fa;}public static int find(int j){if(j==fa[j])return j;else{fa[j] = find(fa[j]);return fa[j];}}
}答案
import java.util.Scanner;public class Main {private static int[] father;public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt(); // 節點數量int m = scanner.nextInt(); // 邊的數量// 初始化并查集father = new int[n + 1];init(n);// 讀取邊并構建并查集for (int i = 0; i < m; i++) {int s = scanner.nextInt();int t = scanner.nextInt();join(s, t);}int source = scanner.nextInt(); // 起始節點int destination = scanner.nextInt(); // 目標節點// 判斷是否在同一個集合中if (isSame(source, destination)) {System.out.println(1);} else {System.out.println(0);}}// 并查集初始化private static void init(int n) {for (int i = 1; i <= n; i++) {father[i] = i;}}// 并查集里尋根的過程private static int find(int u) {if (u != father[u]) {father[u] = find(father[u]);}return father[u];}// 判斷 u 和 v 是否找到同一個根private static boolean isSame(int u, int v) {return find(u) == find(v);}// 將 v -> u 這條邊加入并查集private static void join(int u, int v) {int rootU = find(u);int rootV = find(v);if (rootU != rootV) {father[rootV] = rootU;}}
}







)




)

Bagging)



)

