一、題目描述
給你鏈表的頭結點?head?,請將其按?升序?排列并返回?排序后的鏈表?。
示例 1:
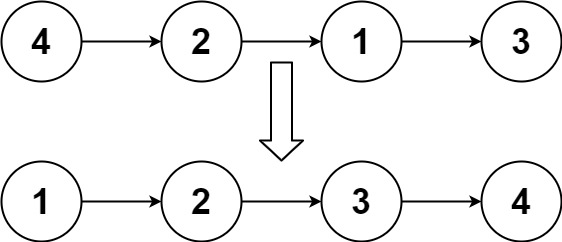
輸入:head = [4,2,1,3] 輸出:[1,2,3,4]
示例 2:
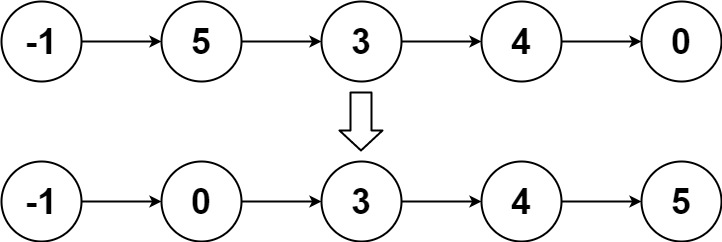
輸入:head = [-1,5,3,4,0] 輸出:[-1,0,3,4,5]
示例 3:
輸入:head = [] 輸出:[]
提示:
- 鏈表中節點的數目在范圍?
[0, 5 * 10^4]?內 -10^5?<= Node.val <= 10^5
二、解題思路
要解決這個問題,我們可以使用歸并排序,這是一種適合鏈表的排序算法,因為鏈表的元素在內存中不是連續存儲的,歸并排序不需要額外的存儲空間,且時間復雜度為O(n log n),是一種效率較高的排序算法。
歸并排序的基本思想是將鏈表分成兩半,分別對這兩半進行排序,然后將排序好的兩部分合并在一起。在鏈表中實現這一思想相對簡單,因為只需要改變節點的next指針即可完成排序。
以下是使用歸并排序對鏈表進行排序的步驟:
- 找到鏈表的中點,可以使用快慢指針法。
- 將鏈表從中點斷開,形成兩個子鏈表。
- 對兩個子鏈表分別進行遞歸排序。
- 將兩個已排序的子鏈表合并在一起。
三、具體代碼
class Solution {public ListNode sortList(ListNode head) {if (head == null || head.next == null) {return head;}// Step 1. 分割鏈表ListNode slow = head, fast = head.next;while (fast != null && fast.next != null) {slow = slow.next;fast = fast.next.next;}ListNode mid = slow.next;slow.next = null;// Step 2. 遞歸排序ListNode left = sortList(head);ListNode right = sortList(mid);// Step 3. 合并鏈表return merge(left, right);}private ListNode merge(ListNode l1, ListNode l2) {ListNode dummy = new ListNode(0);ListNode current = dummy;while (l1 != null && l2 != null) {if (l1.val < l2.val) {current.next = l1;l1 = l1.next;} else {current.next = l2;l2 = l2.next;}current = current.next;}if (l1 != null) {current.next = l1;} else {current.next = l2;}return dummy.next;}
}
四、時間復雜度和空間復雜度
1. 時間復雜度
- 分割鏈表:使用快慢指針找到中點的時間復雜度是O(n),其中n是鏈表的長度。
- 遞歸排序:將鏈表分割成兩半,每半的長度大約是n/2,因此遞歸的深度是O(log n),每次遞歸調用需要對兩個子鏈表進行合并,合并的時間復雜度是O(n),所以遞歸排序的總時間復雜度是O(n log n)。
- 合并鏈表:合并兩個有序鏈表的時間復雜度是O(n),因為每個節點最多被訪問一次。
- 綜上所述,整個算法的時間復雜度是O(n log n)。
2. 空間復雜度
- 遞歸棧空間:由于歸并排序是遞歸進行的,所以需要遞歸棧空間。遞歸的最大深度是O(log n),每個遞歸調用需要常數空間,所以遞歸棧空間的總空間復雜度是O(log n)。
- 合并鏈表:合并鏈表時,除了輸入的鏈表節點外,只需要一個啞節點和幾個指針,不需要額外的空間,因此合并鏈表的空間復雜度是O(1)。
- 綜上所述,整個算法的空間復雜度是O(log n),主要取決于遞歸棧的空間消耗。
綜合以上分析,歸并排序鏈表的算法時間復雜度是O(n log n),空間復雜度是O(log n)。
五、總結知識點
1. 鏈表的基本操作:
- 節點構成:鏈表由節點組成,每個節點包含數據和指向下一個節點的引用。
- 創建與遍歷:鏈表的創建通過連接節點實現,遍歷則是通過依次訪問節點的引用。
- 分割與合并:鏈表的分割通過調整節點的引用實現,合并則是將兩個鏈表的節點按特定順序連接。
2. 遞歸:
- 函數自調用:遞歸允許函數調用自身,用于解決可以分解為更小相似問題的大問題。
- 分治策略:在歸并排序中,遞歸用于將鏈表分成更小的部分,分別排序后再合并。
3. 快慢指針:
- 中點查找:快慢指針技術用于找到鏈表的中點,快指針每次移動兩步,慢指針移動一步。
- 鏈表分割:當快指針到達鏈表末尾時,慢指針所指即為鏈表的中點,從而實現鏈表的分割。
4. 歸并排序:
- 分治算法:歸并排序是一種分治算法,將數據分為兩半,分別排序后再合并。
- 時間復雜度:歸并排序的時間復雜度為O(n log n),適用于鏈表排序。
5. 合并有序鏈表:
- 比較與連接:合并兩個有序鏈表時,比較節點值,將較小的節點連接到結果鏈表中。
- 鏈表拼接:當一個鏈表為空時,將另一個鏈表的剩余部分接到結果鏈表的末尾。
6. 啞節點:
- 輔助節點:啞節點作為輔助節點,用于簡化鏈表操作的邊界條件處理。
- 處理頭節點:在合并鏈表時,使用啞節點作為結果鏈表的起始節點,避免處理頭節點的特殊情況。
以上就是解決這個問題的詳細步驟,希望能夠為各位提供啟發和幫助。
、封鎖協議(兩階段封鎖協議))






)
)
-- Sharding-JDBC 水平分庫 和 垂直分庫。)









)