引言

• 昨天主要是面試，然后剩下的時間都是用來對面試中不會的東西進行查漏補缺，順便和同學聚會。今天繼續把算法做了。

• 總覺得自己的進度還是太慢了，項目不整理出來，連簡歷都沒有辦法修改，這里得加快一下進度，然后今天除了刷算法，主要是干兩件事

  • 整理想去參加的暑期openday，記錄在表格中
  • 繼續準備項目，并且根據項目完善自己的簡歷。

• 動態規劃基本上已經全部做完了，今天能夠最后幾題收個尾，練了那么久，基本上都能夠做出來。

復習

新作

1143-最長公共子序列

題目鏈接

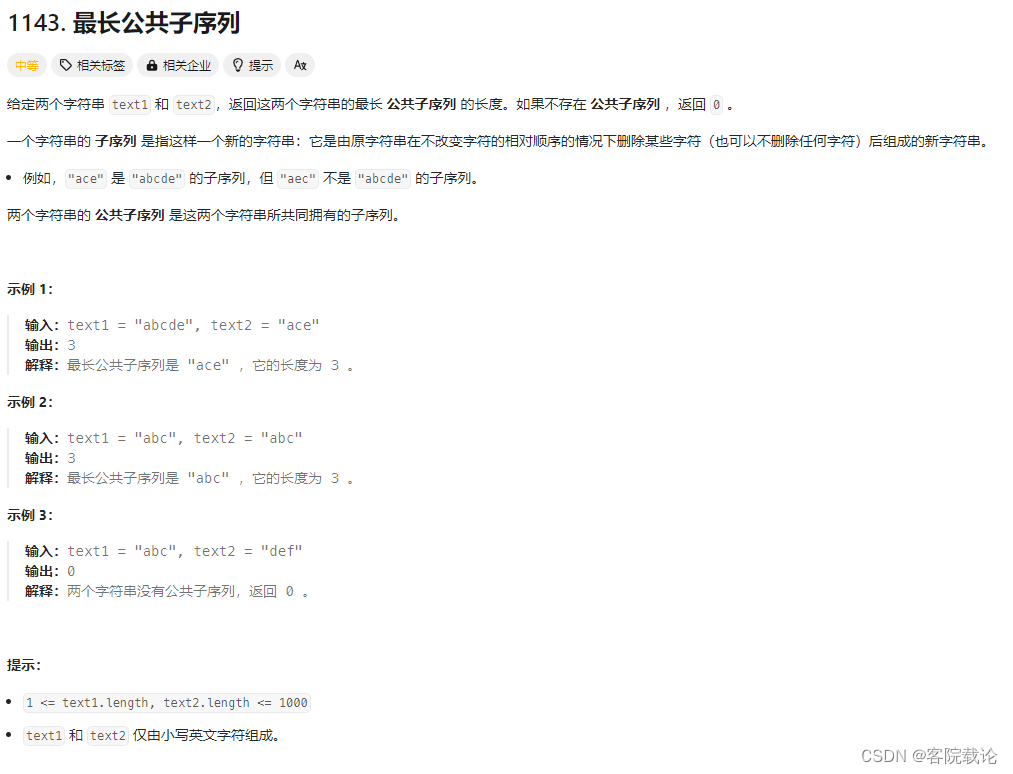
注意

• 都是小寫英文字母組成==》可以使用ACSCII碼進行操作
• 字符串的長度從1到1000==》注意邊界條件
• 子序列==》不改變原始序列中字符相對位置的情況下，刪除一部分的元素
  • abcde==》ade
• 返回最長公共子序列的長度，沒有返回零

個人實現

• 這道題不在之前任何一個模板里面，沒什么思路，只能自己使用集合的角度去考慮問題，想想看。

• 單純使用暴力搜索的算法是怎么做的？

  • 如何提取出一個字符串的子串？每一個字符存在兩種情況，加入或者不加入，假設有n個字符，那就是的2的n次方個字串了，這個問題規模太大了。何況是兩個字符串
  • 假設能夠將兩個字符串的所有子串都提取出來，那么再一個一個匹配，就是$2^n$ * $2^n$，然后在比較獲取最長的長度，這樣問題規模就已經爆炸了。

• 在轉換一下，最長的子串，肯定是建立在較短的字符子串上面的

  • 任何一個字符串新增加一個字母，都有可能會改變的最終匹配的字符串的長度
  • 如何從短的字符串過渡到長的字符串？使用什么方法？或者表達式？兩個字符串，是不是需要從兩個維度進行考慮f[i][j],分別表示的兩個字符串對應到對應索引的位置，然后最長的公共子串長度？但是有一個問題，就是你需要記錄的是匹配的字符串長度的索引，然后一旦后續有變化，在往后面的索引繼續增加就行了。

具體推導，看是看圖吧，如下圖，是我自己的推導

• 整理出來了，但是沒有使用集合的角度去分析，但是大概的邏輯是對的就行了，先做著吧。時間復雜度就是m*n

class Solution {
public:int longestCommonSubsequence(string t1, string t2) {int m = t1 n = t2;vector<vector<int>> f(t1,f(t2,0));vector<vector<int>> td1(t1,f(t2,0));vector<vector<int>> td2(t1,f(t2,0));// 遍歷對應的索引位置for(int i = 0;i < m;i ++){for(int j = 0;j < n;j ++){// 多種情況，分別是僅僅增加i、僅僅增加j或者兩者同時增加if(i) f[i][j] = max(f[i][j],f[i-1][j]+commonSeq(t1.substr(td1[i - 1][j],i),t2.substr(td2[i - 1][j],j)))if(j) f[i][j] = max(f[i][j],f[i][j-1]+commonSeq(t1.substr(td1[i][j-1],i),t2.substr(td2[i][j-1],j)))if(i && j) f[i][j] = max(f[i][j],f[i-1][j-1]+commonSeq(t1.substr(td1[i-1][j-1],i),t2.substr(td2[i-1][j-1],j)))// 還需要更新最后兩者索引相同的最后的索引，方便下次調用。// 這里得更新兩次，不過還是能做的，如果能夠寫完，還是對的。}}}
};

總結

• 整理思路加上畫圖，以及最后的寫代碼，差不多用了半個小時，還是沒寫完，不過嚴格按照時間限定出發，沒做出來，不過我覺得我的思路大體還是對的。
• 有一個問題
  • 單獨增加一個和單獨增加多個，沒有任何意義，因為能夠增加多個，就是表示兩個數組都沒有遍歷完，所以還是有問題的。

思路有問題，實現不了

參考實現

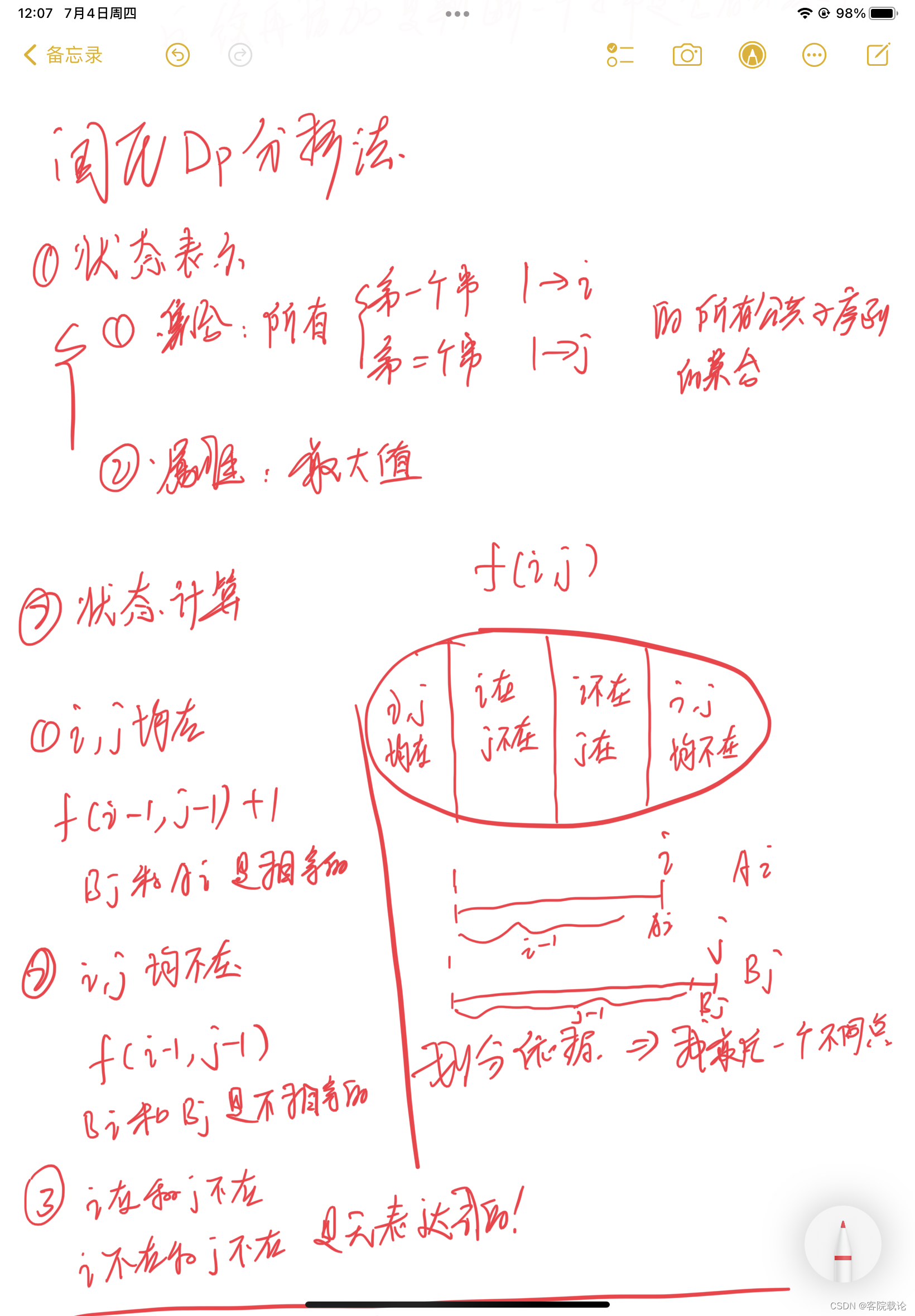
• 思路和我分析的還是比較相似的，只不過我有一個問題，就是沒有意識到如果相同就加一，不同就不變，然后任何一個狀態都是從最初的狀態一步一步迭代過來，就像我之前的推理一一樣，最基礎的這個問題的形態我沒有搞清楚。
• 狀態當成主要有兩個作用
  • f[i][j] = f[i - 1][j - 1] + 1這個是表示對應的相同的迭代情況。
  • 其余的不變就是， 是為了把狀態不斷延續下去，這個原理有的時候并不好想，也比較難想，我就是這里沒有想出來，確實是一個問題。

疑難解答

• 之前還是有一個問題，就是如何保證，A列表加入一個新元素之后，另外一個列表不增加新的元素，然后新增加的元素會帶來更多公共子串
• 不用擔心，這里正常每一個字符串都會相互匹配一次，下一次兩者 相同的時候，一定會加上這個情況
  • 對于那種單個邊相加的，只需要考慮上一個狀態是怎么計算的就行了。

下面是我參考他的思路寫的代碼

class Solution {
public:int longestCommonSubsequence(string t1, string t2) {int m = t1.size(), n = t2.size();vector<vector<int>> f(m + 1,vector<int>( n + 1,0));t1 = " " + t1;t2 = " " + t2;// 遍歷對應的索引位置for(int i = 1;i <= m;i ++){for(int j = 1;j <= n;j ++){// 這里是單邊相加if(t1[i] != t2[j]) f[i][j] = max(f[i][j-1],f[i-1][j]);else f[i][j] = f[i - 1][j - 1] + 1;}}return f[m][n];}
};

• 這里并不知道如何處理索引為0的情況，所以這里在開頭增加了一個空格

再參考修改

• 這里使用i- 1來判定是否相等就可，很聰明，跟之前個優先隊列的提前試探一樣。

class Solution {
public:int longestCommonSubsequence(string t1, string t2) {int m = t1.size(), n = t2.size();vector<vector<int>> f(m + 1,vector<int>( n + 1,0));// 遍歷對應的索引位置for(int i = 1;i <= m;i ++){for(int j = 1;j <= n;j ++){// 這里是單邊相加f[i][j] = max(f[i][j-1],f[i-1][j]);if(t1[i- 1] == t2[j - 1]) f[i][j] = f[i - 1][j - 1] + 1; }}return f[m][n];}
};

下面再leetcode上摘抄的一部分矩陣關系變化圖很有參考意義

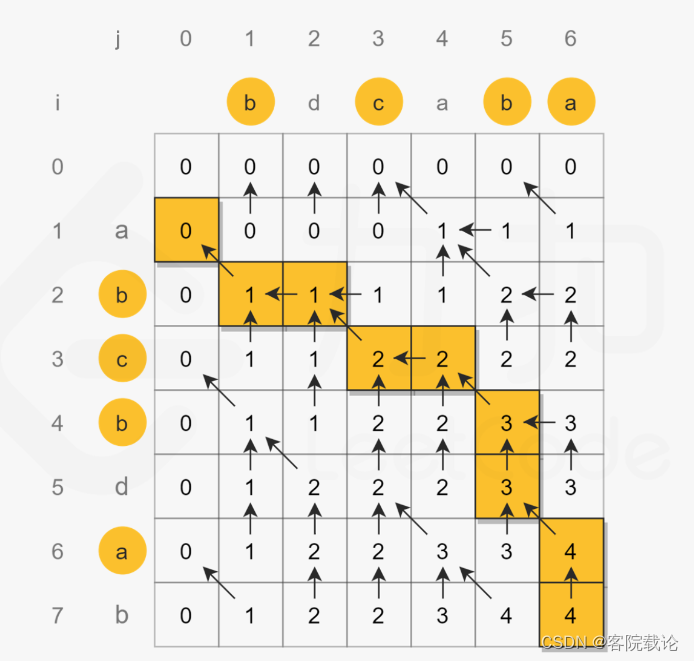
編輯距離

• 題目鏈接

注意

• 只有三種操作
  • 插入一個新的字符==》任何位置插入元素
  • 刪除原來的字符==》刪除任何位置的元素
  • 替換對應的字符
• 將一個單詞變成另外一個單詞的最小操作次數

個人實現

• 首先，如果對這道題的狀態限定一下，保證每一個操作之后都有固定的三種操作，就變成一個三叉樹，然后進行廣度優先遍歷深度，是可以解決問題的，但是現在是不限定的每一層的節點數或者分支數，這個是完全沒有辦法的使用類似的方法。

• 首先，我們先來看看最多操作，也沒有一個通用的算法，因為單詞的長度的不一樣。

  • 目標長度單詞小于當前的單詞，那就先刪除，保證長度是一致的，然后在替換，這個是最直接的。
  • 目標長度單詞大于當前的單詞，那就先添加，保證的長度一致的，然后再替換，結果最直接。

• 上述方法很好實現，除此之外，我還需要確定一件事，就是刪除元素之后，是否能夠保證后續的元素會自動跟上，如果是的話，那么這個問題就變了，刪除特定位置的元素，也能夠實現單詞轉換。

• 動態規劃，沒什么思路，甚至集合都不知道怎么操作，屬性表達式倒是很好說明

  • f[i][j],把字符串從i變成j，所有的方案各自的步驟數量
  • 屬性是最小的步驟數
  • 狀態轉換不知道了，不過和上面那道題有點像

下面的方法純屬胡扯了，沒有任何必要

class Solution {
public:int minDistance(string a, string b) {int m = a.size(),n = b.size();vector<vector<int>> f(m +1 ,vector<int>(n + 1,0));for(int i =1;i <= m; i++){for(int j = 1;j <= n;j ++){if(a[i-1] == a[j-1])// 相同的話，刪除中間所有的元素if(i != j)  f[i][j] = f[i - 1][j - 1] + abs(i - j);else// 不同直接刪除f[i][j] = f[i][j] = f[i - 1][j - 1] + 1;}}return f[m][n];}
};

忽然間有思路了，想起來了

• 計算最長公共子串的數量len，具有如下的等式關系
• 如果tar == len，直接返回sour - tar
• 如果tar > len,
  • sour > tar
  • sour < tar
• 如果tar < len,
  • sour > tar
  • sour < tar

上述幾種情況需要好好理理，應該是能夠解決這個問題的，但是今天又超過時間了，直接看解答。

參考實現

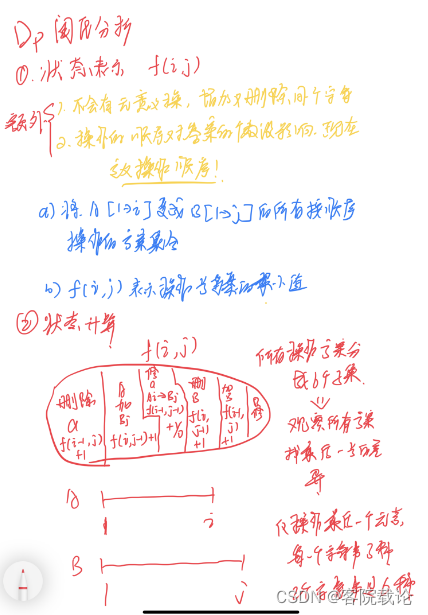
• 這道題就是屬于完全想的不對，但是這種雙類型的字符串的，都有一個訣竅，就是兩個維度，并且都是從最后的一個元素開始考慮的，而且之前的所有元素，都是已經滿足條件的，不要有額外的特殊情況。
• 這里就是假設除了最后一個元素都是匹配的，所以要對最后一個元素進行討論和考慮，按照順序執行三種操作即可
  • 刪除最后一個元素，就能保證兩個字符串匹配，所以被刪除的字符串的前面的所有字符串都是匹配的，f[i][j] = f[i - 1][j] + 1
  • 增加一個新的元素，就能保證最后兩個字符串是匹配的，并且添加地元素就是目標的最后一個元素，Bj，所以狀態轉移就是f[i][j] = f[i ][j- 1] + 1
  • 替換掉對應的元素，兩個元素都不相等
  • 兩個元素相等，無操作

實現代碼

class Solution {
public:int minDistance(string a, string b) {int m = a.size(),n = b.size();vector<vector<int>> f(m +1 ,vector<int>(n + 1,INT_MAX));a = " " + a;b = " " + b;// 初始化邊界條件for(int i = 0;i <= m;i ++)  f[i][0] = i;     // 目標字符串是空的，刪除操作若干次for(int i = 1;i <= n;i ++)  f[0][i] = i;  // 當前字符串是空的，目標字符串的是有長度的，添加若干次for(int i =1;i <= m; i++){for(int j = 1;j <= n;j ++){f[i][j] = min(f[i-1][j],f[i][j-1]) + 1;int t = a[i] != b[j];f[i][j] =min(f[i][j], f[i - 1][j - 1] + t);}}return f[m][n];}
};

總結

• 為什么總是寫不出來，我覺得是因為我看問題的角度和他的不一樣，他的問題角度是最后一個元素就能保證當前狀態完全成立，但是我會被困在中間狀態，改變不了，還是改變一下。
• 這里的邊界條件處理也很特殊，需要根據實際情況盡心處理。

貪心——買股票的最佳時機

題目鏈接

注意

• 計算能夠獲取的最大利潤
• 當天買入，然后后續的某一天賣出，計算差價

個人實現

• 這道題就是爽題，單純是一道狀態機模型，是DP，爽題。

class Solution {
public:int maxProfit(vector<int>& prices) {vector<int> buy(prices.size() + 1,-1e6); // 持有狀態：vector<int> sell(prices.size() + 1,-1e6);  // 無持有狀態buy[0] = 0 - prices[0];sell[0] = 0;for(int i = 1;i < prices.size();i ++){buy[i] = max(sell[i -1] - prices[i],buy[i-1]);sell[i] = max(sell[i - 1],buy[i - 1] + prices[i]);}return sell[prices.size()-1];}
};

給我整麻了，看錯題了，這里是只能買入一次，然后賣出一次，不是可以操作多次

• 只能操作一次，那么直接暴力搜索就行了，平方的時間復雜度，會超時，在想想哈.

弄成下面這樣，慘不忍睹

class Solution {
public:int maxProfit(vector<int>& prices) {int res = 0;vector<pair<int,int>> f(prices.size());for(int i = 0;i < prices.size();i++) {if(i + 1 < prices.size() && prices[i] == prices[i + 1]) continue;f.push_back({prices[i],i});}sort(f.begin(),f.end(),[](auto a,auto b){return a.first > b.first;});for(int i = 0;i < prices.size();i ++){if(i + 1 < prices.size() && prices[i] == prices[i + 1]) continue;// 找到往后小的元素for(auto x : f) if(x.second > i ) {res = max(res,x.first - prices[i]);break;}  }return res;}
};

參考實現

• 這個思路感覺很清晰，但是我沒有想到，感覺就是差點，
• 找到對于第i天的歷史最低點，然后計算利潤即可。遍歷一次是可以記錄歷史最低點的，然后反復計算對應的利潤就行了

class Solution {
public:int maxProfit(vector<int>& prices) {int minPrice = INT_MAX,maxPrift = 0;for(int i = 0;i < prices.size();i ++){if(prices[i] < minPrice)    minPrice = prices[i];else{maxPrift = max(maxPrift,prices[i] - minPrice);}}return maxPrift;}
};

貪心——55-跳躍游戲

題目鏈接

注意

• 一開始位于第一個下標
• 數組的值表示你最多可以跳的次數，你可以選擇[0,value]的任意一個數值作為你跳的步驟
• 數組長度邊界值為一，可以跳過
• 每一個值可以為零，最大沒有越界

個人實現

• 從當前的位置出發能不能到達目標點，直接使用暴力進行搜索可以試試看，遍歷所有情況，如果能夠找到目標點，就返回true
• 時間復雜度：最多是$10^9$，應該會超時，但是可以進行剪枝，先寫出來再說
• 使用dfs遞歸實現，具體實現如下

十五分鐘寫成這樣，超時，只能通過一半的樣例，不行

class Solution {
public:bool dfs(vector<int> nums,int idx){// 等于目標值，直接返回if(idx == nums.size() - 1)  return true;for(int i = nums[idx];i >= 1;i --){if(idx + i < nums.size() && dfs(nums,idx + i))   return true; }return false;}bool canJump(vector<int>& nums) {if(nums.size() == 1)    return true;if(nums[0] == 0 )   return false;// 正常情況，第一個數值不為零，并且長度超過了一return dfs(nums,0);}
};

可以將問題拆解一下，先拆成到中間某一個節點的情況

是不是思路有問題，不應該使用模擬的方式。發現了，特殊情況時針對0而言的，只要有一個非零的數字，就能夠一直往下走，所以按照零進行分段就行。

class Solution {
public:// 遞歸調用bool dfs(vector<int> nums,int idx){// 等于目標值，直接返回if(idx == nums.size() - 1)  return true;for(int i = nums[idx];i >= 1;i --){if(idx + i < nums.size() && dfs(nums,idx + i))   return true; }return false;}bool canJump(vector<int>& nums) {if(nums.size() == 1)    return true;if(nums[0] == 0 )   return false;int dis = 0,sp = 0;for(int i = 0;i < nums.size() -1;i ++){if(nums[i] != 0) dis = max(dis,nums[i]);else{cout<<i<<sp<<endl;if(i - sp > dis)  { return dfs(nums,i - 1);}                else sp = i;}}return true;}
};

寫的這個還是有問題，不倫不類的，將兩個都結合了，還有問題，不過我發現，判斷還是有問題的，其實不需要看整個，只需要看，零前面的那個數字是多少就行了，能不能蓋過零。綜合來判定，我的思路沒考慮到，時間不夠，認輸

參考做法

• 這里跟我的思路很想，但是我沒有考慮地很周全，是計算每一個點所能夠訪問的最遠距離，如果i超過了能夠訪問的最遠距離，就表示訪問不到，直接跳過。
• 最遠距離更新方式
  • 判定當前的i是否可以訪問到
  • j = max(i + nums[i],j);

很直觀的做法，沒考慮到

class Solution {
public:bool canJump(vector<int>& nums) {for(int i = 0,j = 0;i < nums.size();i ++){// i超過了最遠距離，不能訪問了if(i > j)   return false;// 沒有超過最遠距離，需要進行更新j = max(i + nums[i],j);}return true;}
};

總結

• 今天的進度有點慢了，為什么會這么慢，上午就刷了兩道題，是因為什么？中間洗了一下衣服，然后刷了一會視頻，不行，還是有點來不及。下午吃飯快點，多留點時間。
• 真的難呀，一天天的，不如開機重啟！
• 難受呀，晚上兩道題，沒有一道題是按時AC的，那道簡單題還看錯題目了，然后花了很多時間，結果簡答的思路都沒有考慮到。不過無所謂了，學到了，練習到了，今天又刷了四道題，明天繼續加油！