目錄
The Impact of Management Training
Adjusting with Regression
之前學習了如何使用線性回歸調整混雜因素。此外,還向您介紹了通過正交化去偏差的概念,這是目前最有用的偏差調整技術之一。不過,您還需要學習另一種技術--傾向加權。這種技術涉及對治療分配機制進行建模,并利用模型的預測對數據重新加權,而不是像正交化那樣建立殘差
本文內容更適合于有二元或離散干預的情況。不過,我還是會展示一種擴展方法,讓你可以將傾向加權用于連續干預。
The Impact of Management Training
科技公司的一個普遍現象是,有才華的個人貢獻者(IC)會向管理層發展。但是,由于管理層所需的技能往往與他們成為優秀個人貢獻者的技能大相徑庭,因此這種轉變往往絕非易事。不僅對新任管理者,而且對他們所管理的人員來說,都要付出高昂的個人代價。
一家大型跨國公司希望減少這種過渡的痛苦,決定投資對新任經理進行經理培訓。同時,為了衡量培訓的效果,該公司嘗試隨機挑選經理人參加這一項目。我們的想法是,比較那些經理參加了培訓的員工與那些經理沒有參加培訓的員工的敬業度得分。通過適當的隨機化,這種簡單的比較就能得出培訓的平均干預效果。
遺憾的是,事情并沒有那么簡單。有些經理不想參加培訓,就干脆不來了。還有一些人即使沒有被指定接受培訓,也設法接受了培訓。結果,本來是一項隨機研究,到頭來卻變成了觀察研究。
現在,作為一名必須閱讀這些數據的分析師,你必須通過調整混雜因素,使治療和未治療的數據具有可比性。為此,你會得到有關公司經理的數據以及描述他們的一些協變量:
import pandas as pdimport numpy as npdf = pd.read_csv("data/management_training.csv")df.head()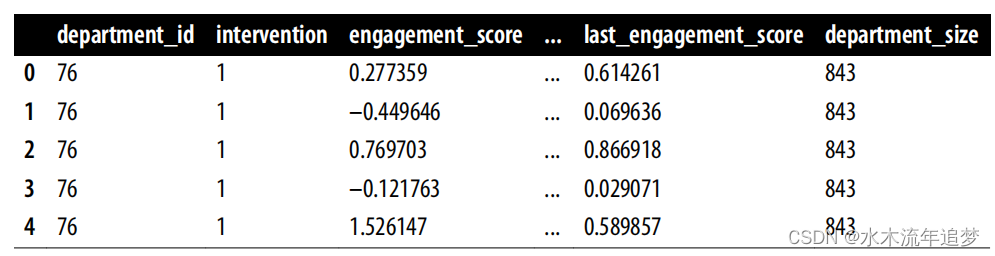
處理變量是intervention,您感興趣的結果是 engagement_score,即該經理的員工的平均標準化敬業度得分。除了干預和結果之外,該數據中的協變量還有
Adjusting with Regression
在進行傾向加權之前,我們先用回歸法來調整混雜因素。一般來說,在學習新知識時,最好能有一些值得信賴的基準進行比較。這里的想法是檢查傾向加權估計值是否至少與回歸估計值一致。現在,讓我們開始吧。
首先,如果只是比較治療組和對照組,您會得到以下結果:
import statsmodels.formula.api as smfsmf.ols("engagement_score ~ intervention",data=df).fit().summary().tables[1]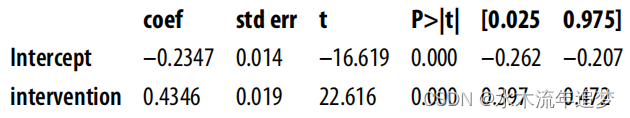
但話說回來,這個結果很可能是有偏差的,因為干預并非完全隨機。為了減少這種偏差,您可以根據數據中的協變量進行調整,估計出以下模型:
其中,X 為所有混雜因素,加上一列常數作為截距。此外,性別和角色都是分類變量,因此您必須在 OLS 公式中用 C() 將它們包起來:
model = smf.ols("""engagement_score ~ intervention + tenure + last_engagement_score + department_score+ n_of_reports + C(gender) + C(role)""", data=df).fit()print("ATE:", model.params["intervention"])print("95% CI:", model.conf_int().loc["intervention", :].values.T)ATE: 0.267790857667685695% CI: [0.23357751 0.30200421]請注意,這里的效果估計值比您之前得到的效果估計值要小得多。這在一定程度上表明存在正偏差,即員工參與度已經較高的經理更有可能參加了經理培訓項目。好了,前言到此為止。讓我們來看看傾向加權是怎么回事。






)

)


![安卓請求服務器[根據服務器的內容來更新spinner]](http://pic.xiahunao.cn/安卓請求服務器[根據服務器的內容來更新spinner])







