1. 二分查找（704）

題目描述：

算法原理：
暴力解法就是遍歷數組來找到相應的元素，使用二分查找的解法就是每次在數組中選定一個元素來將數組劃分為兩部分，然后因為數組有序，所以通過大小關系舍棄一部分數組，最終不斷重復這個過程完成查找，時間復雜度可以達到logN。
代碼如下：

class Solution {public int search(int[] nums, int target) {int left = 0;int right = nums.length-1;while (right >= left) {int mid = left + (right - left) / 2;if (nums[mid] > target) {right = mid - 1;} else if (nums[mid] < target) {left = mid + 1;} else {return mid;}}return -1;}
}

題目鏈接

2. 在排序數組中查找元素的第一個和最后一個位置（34）

題目描述：

樸素二分查找：
這題我們可以先使用樸素二分查找的方法取找到等于target的元素下標，此時再分別使用兩個循環去比較左右兩邊元素是否與target相等，如果相等則分別向左和向右移動，最終返回對應的下標即可，這個過程很好理解。
代碼如下：

class Solution {public int[] searchRange(int[] nums, int target) {int left = 0, right = nums.length - 1;int index1 = -1, index2 = -1;while (left <= right) {int mid = left + (right - left) / 2;if (nums[mid] < target) {left = mid + 1;} else if (nums[mid] > target) {right = mid - 1;} else {index1 = mid;index2 = mid;while (index1 - 1 >= 0 && nums[index1] == nums[index1 - 1]) {index1--;}while (index2 + 1 < nums.length && nums[index2] == nums[index2 + 1]) {index2++;}break;}}return new int[] { index1, index2 };}
}

優化樸素二分查找：
首先我們去尋找target的左邊界，為了便于理解我們給出圖1，數組的元素可以分為兩個部分，前半部分是小于target的元素，后一部分是大于等于target的部分。
圖1

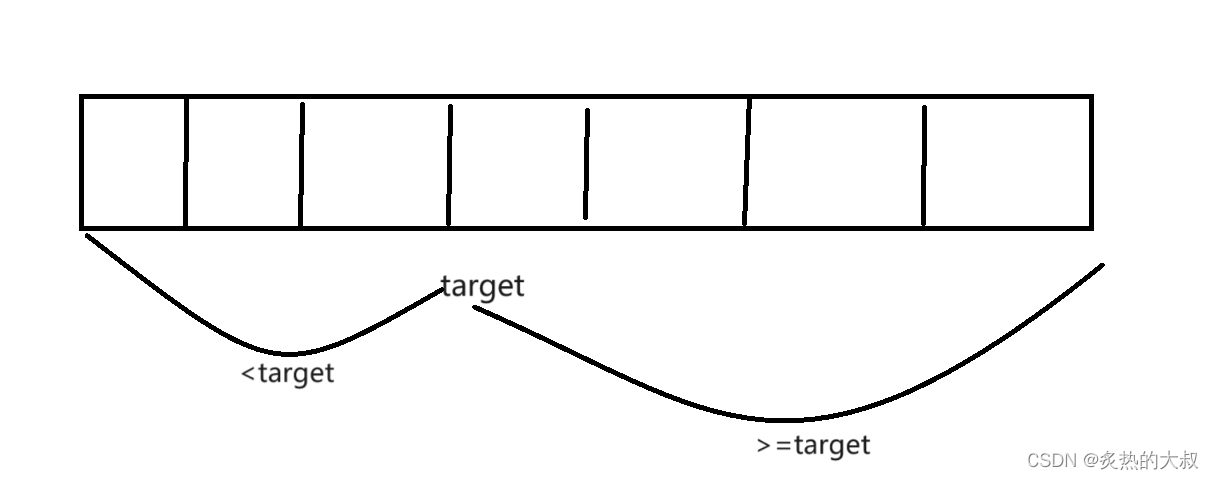
如圖2，當我們的nums[mid]也就是x落入前半部分的時候，為了去接近target需要使得left=mid+1，當我們的x落入后半部分的時候，此時我們不能夠使right=mid-1，因為如果說此時x是等于target的并且是左邊的最后一個target，那么將right-1后面就直接再也找不到正確的target了。綜上，如果x落入圖1的第二段區間，那么就使得right=mid。很好理解的一點就是通過這樣的操作，left在不斷的向右移動，right在不斷的向左移動但是它的下標也不會超出圖1第二段區間的左邊，這樣我們就能夠找到連續target的左邊界。
圖2

然后我們來處理兩個細節問題，第一個問題就是這樣使用二分查找，它的循環條件是使用left<right還是left<=right。我們樸素二分查找是使用后者的，但是在這里要使用前者。為什么呢，這里先分三種情況：
（1）target在right和left區間之內
在這種情況下，最終right會等于left，此時跳出循環即可，直接得到的下標就是正確答案，根本不需要去額外在循環當中去分三種情況> < ==。
（2）left和right區間內都是小于target的
此時left不斷的加一最終和right相等跳出循環即可，然后判斷nums[right]是否等于target。
（3）left和right區間內都是大于target
此時right不斷向右最終和left相等跳出循環。
以上是選擇left<right的原因之一，另一個原因就是使用left<=right會造成死循環，當我們使用圖2中的方法來處理最終得到結果時，此時left等于right，如果使用left<=right下一次不會跳出而是會進入死循環，這一點還是很好理解的。
綜上三種情況，我們使用left<right這樣的循環條件，是因為當跳出循環時我們可以進行判斷nums[right]是否等于target從而直接得到結果，另外可以防止死循環。
第二個細節問題就是中點的選擇，一般是有兩種方式來計算中點如圖3。
圖3

圖3中兩種計算中點的方式在樸素二分查找中都是可以適用的，但是這里也就是按照圖2的計算方式來說兩種方式是有差別的，如果我們使用第二種計算方式，如果我們將left和right的區間縮小到兩個元素，也就是left+1等于right這種情況，此時mid計算為right，nums[mid]等于target，right=mid，后面的循環mid經過計算又等于原來的值，由此進入死循環，為了避免這種情況我們就需要使用第一種計算中點的方式。
以上就是求連續的target左邊界的分析，對于右邊界的分析也是類似的，唯一需要注意的就是此時計算中點的方式要選擇第二種否則會造成死循環。
優化后代碼如下：

class Solution {public int[] searchRange(int[] nums, int target) {int left1 = 0, right1 = nums.length - 1;if (right1 == -1) {return new int[] { -1, -1 };}int[] ret = new int[2];while (left1 < right1) {int mid1 = left1 + (right1 - left1) / 2;if (nums[mid1] < target) {left1 = mid1 + 1;} else {right1 = mid1;}}if (nums[right1] == target) {ret[0] = right1;} else {ret[0] = -1;}int left2 = 0, right2 = nums.length - 1;while (left2 < right2) {int mid2 = left2 + (right2 - left2 + 1) / 2;if (nums[mid2] > target) {right2 = mid2 - 1;} else {left2 = mid2;}}if (nums[left2] == target) {ret[1] = left2;} else {ret[1] = -1;}return ret;}
}

解題模板：

下面出現減一上面就需要加一。
題目鏈接

3. 搜索插入位置（35）

題目描述：

算法原理：
根據題目知道，這里的數組是一個升序并且無重復元素的數組，并且如果數組內包含target就求出target的下標，如果數組中不包含target就求出第一個大于target的數的下標，這就是題目的要求。那么我們就可以將數組分為兩部分，第一部分是小于target的部分，第二個部分是大于等于target的部分，那么我們直接求出第二部分的左邊界即可。前面的題目我們也給出了模板以及解題的思路，具體看代碼。
代碼如下：

class Solution {public int searchInsert(int[] nums, int target) {int left = 0, right = nums.length - 1;if (nums[right] < target) {return right + 1;}while (left < right) {int mid = left + (right - left) / 2;if (nums[mid] < target) {left = mid + 1;} else {right = mid;}}return right;}
}

題目鏈接

4. x 的平方根 （69）

題目描述：

算法原理：
根據題目我們知道可以將1到x就當成數組中的數，然后我們需要去找到一個數n去滿足n*n等于x，這個n就可以使用二分查找來進行尋找，將1到x分為兩部分，一部分是數的平方小于等于x另一部分是數的平方大于x，顯然我們只需要找到第一部分的右邊界即可。不過這題提交的時候要注意數據溢出的問題，要確定好數的類型。
代碼如下：

class Solution {public int mySqrt(int x) {if (x == 0) {return 0;}int right = x, left = 1;while (left < right) {long mid = left + (right - left + 1) / 2;if (mid * mid <= x) {left = (int) mid;} else {right = (int) mid - 1;}}return left;}
}

題目鏈接