什么是子序列

在計算機科學和數學中，子序列（Subsequence）是指從一個序列中刪除一些元素（可以是零個或多個），但不改變其余元素相對順序后形成的新序列。

子序列的特點

元素的相對順序保持不變。
可以刪除零個或多個元素。
一個序列的子序列可以為空序列，即不包含任何元素。

舉例說明

設有序列 S = [A, B, C, D, E]，則其子序列可以有：
刪除零個元素：[A, B, C, D, E]（即自身）
刪除一個元素：[A, B, C, D]、[A, B, C, E]、[A, B, D, E]、[A, C, D, E]、[B, C, D, E]
刪除兩個元素：[A, B, C]、[A, B, D]、[A, B, E]、[A, C, D]、[A, C, E]、[A, D, E]、[B, C, D]、[B, C, E]、[B, D, E]、[C, D, E]
刪除三個元素：[A, B]、[A, C]、[A, D]、[A, E]、[B, C]、[B, D]、[B, E]、[C, D]、[C, E]、[D, E]
刪除四個元素：[A]、[B]、[C]、[D]、[E]
刪除所有元素：[]（空序列）

常見問題

子序列問題在算法設計和編程競賽中非常常見。以下是幾種經典問題：
最長公共子序列（LCS）：給定兩個序列，找出它們的最長公共子序列。動態規劃是解決這個問題的常用方法。
最長遞增子序列（LIS）：給定一個序列，找出其中最長的遞增子序列。可以使用動態規劃或貪心算法結合二分查找解決。
子序列和問題：給定一個序列，找出所有和為特定值的子序列。可以使用回溯法或動態規劃解決。

根據我上面的介紹，可以總結，大多數子序列問題其實都可以用DP的算法來解決。

關于子序列問題的幾個例題

1.最長遞增子序列

題目鏈接
題目：

樣例 輸出和輸入：

首先根據上述子序列的描述，這道題就很容易理解了，就是 讓我們求給定數組的最長的遞增子序列。
算法原理：
狀態表示：dp[i]表示以i位置為結尾的所有子序列中最長的那個子序列的長度。
狀態轉移方程：

首先我們要求狀態轉移方程就要看i位置的狀態，我們要確定i位置的狀態，是不是應該將0到i-1位置遍歷一遍，然后將當中的最長子序列求出來然后再加上當前位置的長度1就可以了，這是當子序列長度大于1的時候，還有一種情況是長度等于1的時候，長度等于1的時候，可以默認看做一個子序列，所以dp[i]就等于1，當長度大于1的時候，這種情況，我們先用一個變量j將0到i-1位置的最長子序列遍歷出來，然后再+1，所以狀態轉移方程：dp[i] = max(dp[j]+1,dp[i])。
初始化：因為單獨一個元素就可以看做一個遞增的子序列，所以DP表中的值可以全部初始化為1.
代碼展示：

class Solution {
public:int lengthOfLIS(vector<int>& nums) {int n = nums.size();vector<int> dp(n,1);int dpmax = 1;for (int i = 1;i < n;i++){for (int j = i-1;j >= 0;j--){if (nums[j] < nums[i]){dp[i] = max(dp[j]+1,dp[i]);}dpmax=max(dp[i],dpmax);}}return dpmax;}
};

運行結果：

2.擺動序列

題目鏈接
題目：

樣例 輸出和輸入：

這道題讓我們求擺動序列的最長的子序列的長度，首先我們要搞清楚，什么是擺動序列：

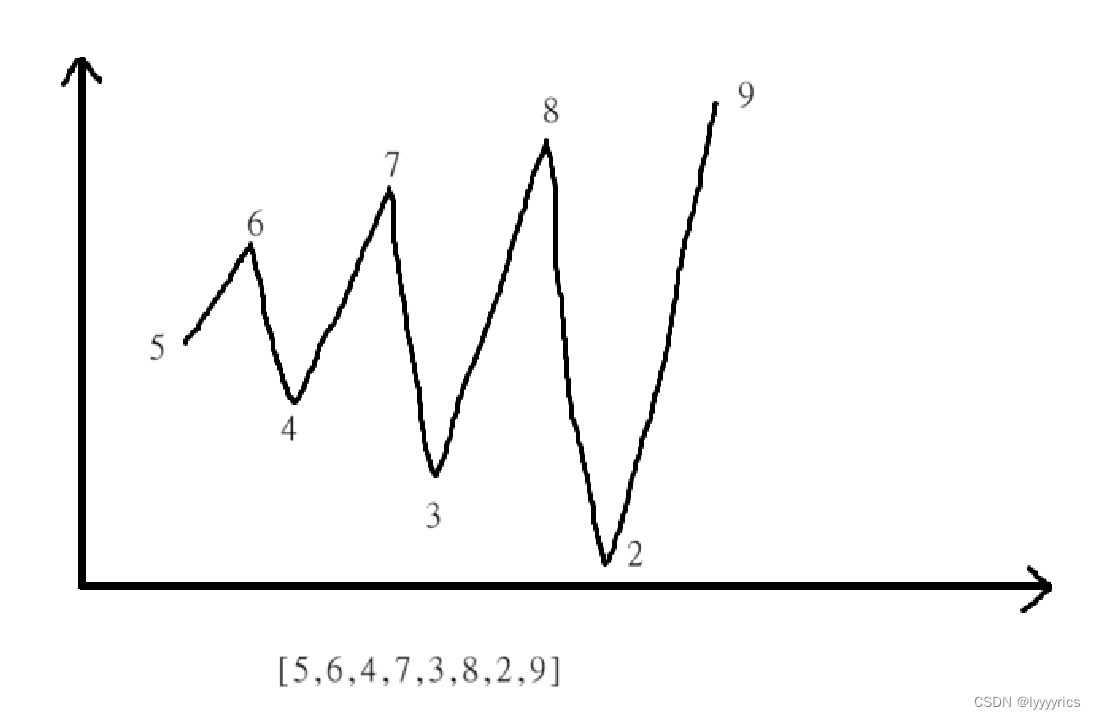
上面就是一個擺動序列。
算法原理：
這道題首先要求擺動序列，我們上個專題已經做過類似的題了，就像湍流數組一樣，這道題很顯然，我們需要兩個狀態，一個狀態是向下的狀態，一個狀態是向上的狀態，這里定義f[i]是向上的狀態，g[i]是向下的狀態。
狀態表示：f[i]是以i位置為結尾的子序列中長度最長且最后一個狀態是向上的最長子序列的長度，g[i]表示以i位置為結尾最后的子序列中最后一個狀態向下的最長子序列的長度。
狀態轉移方程：首先對f[i]分析：
所以這里f[i]的狀態轉移方程：f[i] = max(g[j] + 1, f[i])，同理也可以求出g[i]的狀態轉移方程：g[i] = max(f[j] + 1, g[i])
代碼展示：

class Solution {
public:int wiggleMaxLength(vector<int>& nums) {int n = nums.size();vector<int> f(n,1), g(n,1);int dpmax = 1;for (int i = 1;i < n;i++){for (int j = i - 1;j >= 0;j--){if (nums[j] > nums[i]){g[i] = max(f[j] + 1, g[i]);}else if (nums[j] < nums[i]){f[i] = max(g[j] + 1, f[i]);}dpmax = max(max(dpmax, f[i]), g[i]);}}return dpmax;}
};

運行結果：

3.最長遞增子序列的個數

題目鏈接
題目：

樣例 輸出和輸入：

這道題相對于第一道題換了一個問法。這道題是求最長子序列的個數
算法原理：
狀態表示：首先我們先定義一個狀態，看這個狀態能推下去嗎，dp[i]表示以i位置為結尾的所有子序列中，最長子序列的個數。
狀態轉移方程：首先這里就出問題了 ，這里我們根本不知道最長的子序列是什么，因為根本沒有記錄的，所以這里根本就推不出來，所以還得加一個len[i]，len[i]表示以i位置為結尾的所有子序列中最長子序列的長度，將dp[i]改為count[i]，count[i]表示以i位置為結尾的所有子序列中最長的子序列的個數。接下來來推狀態轉移方程，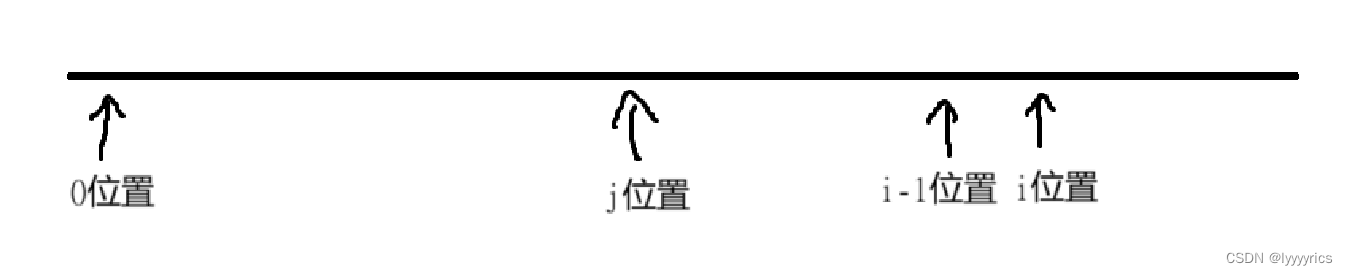
有三種情況，當我們遍歷的len[j]+1==len[i]，意思就是0到i-1位置的子序列中加上當前的長度和之前的最長的子序列是相同的，這里我們應該把以j位置為結尾的最長子序列的個數全部加到count[i]]中。這里畫圖表示

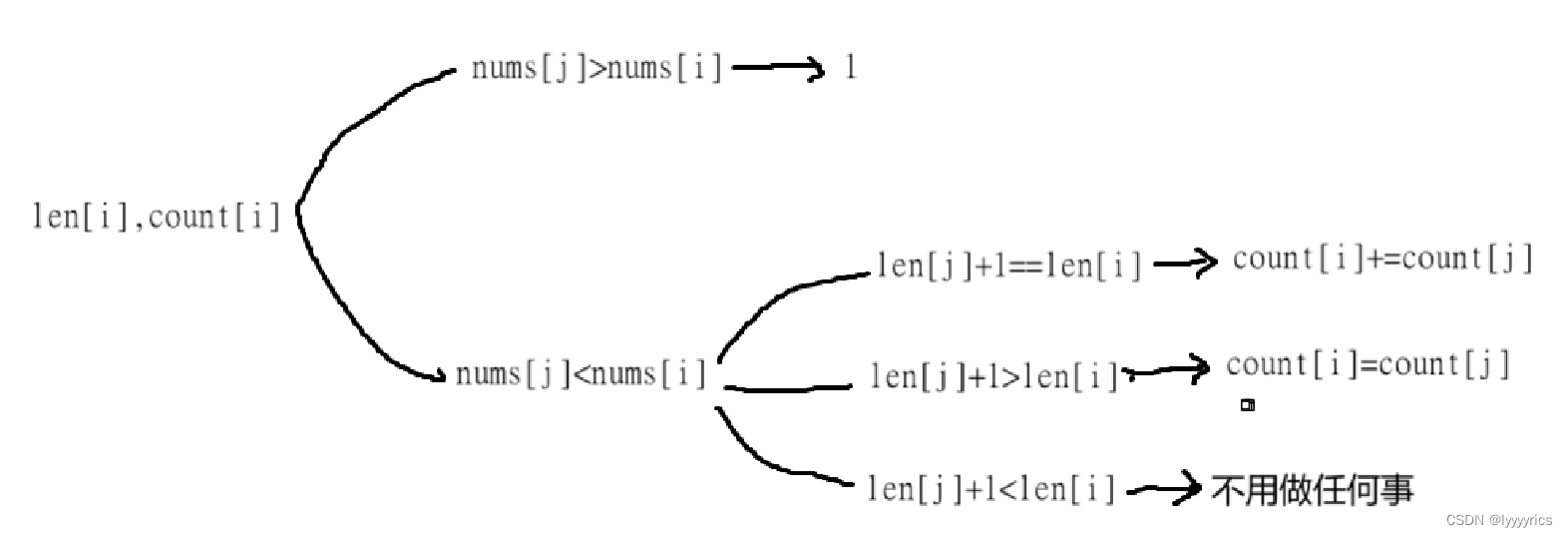
根據這些情況可以將表填完，但是，我們還需要 一個retlen和一個retcount更新每次的最長子序列的長度和最長子序列的個數。
這里也分為三種情況，和上面的情況相同，只需要每次遍歷完一個位置，更新結果即可。

代碼展示：

class Solution {
public:int findNumberOfLIS(vector<int>& nums) {int n = nums.size();vector<int> len(n,1), count(n,1);//統計每次的每次的最終結果int retlen = 1, retcount = 1;for (int i = 1;i < n;i++){for (int j = i - 1;j >= 0;j--){//當出現遞增的時候if (nums[j] < nums[i]){//判斷如果加上遞增的那一個和當前最長的長度還是一樣的則需要更新countif (len[j] + 1 == len[i])count[i] += count[j];//如果加上當前的一個元素比比之前的最長的子序列要長，則重新規劃長度else if (len[j] + 1 > len[i])count[i] = count[j],len[i] = len[j];}}//統計每次的結果，如果len和結果的len相同，則直接用count累加if (retlen == len[i])retcount += count[i];//如果len比結果的len要大，則直接重置結果len和結果的countelse if (retlen < len[i])retcount = count[i], retlen = len[i];}return retcount;}
};

運行結果：

4.最長數對鏈

題目鏈接
題目：

樣例 輸出和輸入：

這道題其實和求最長子序列的長度是相同的題，但是換了一個形式而已，根據題目條件我們可以得知什么是數對鏈：

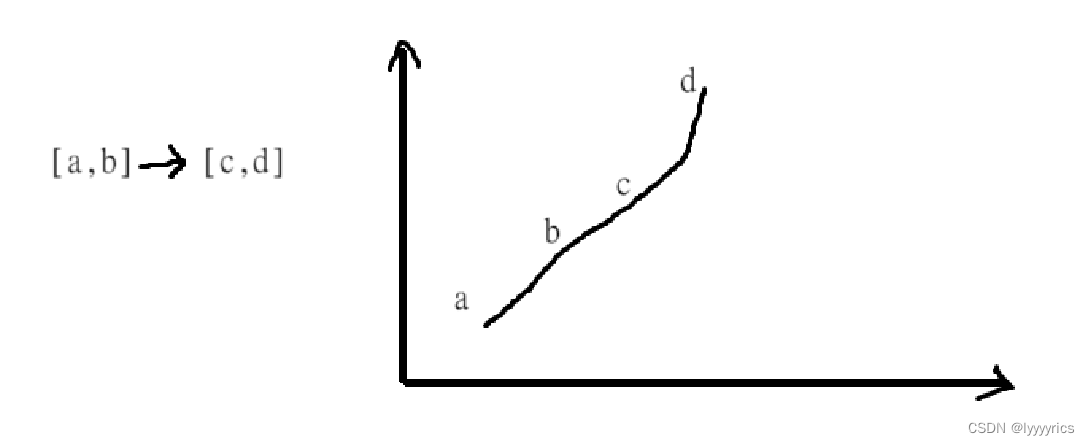
數對連就要滿足上述條件
算法原理：
預處理：首先我們得將數組排序，排序的規則，只需要比較每個數對的第一個元素的大小即可，因為每個數對都是單增的，如果我們排序之后保證了a>c，那么d>c是絕對大于前一個數對的，所以這里只需要根據前一個數排序即可。
狀態表示：這里dp[i]表示以i位置為結尾的所有數對鏈中最長的那個數對鏈的長度。
狀態轉移方程：分兩種情況：

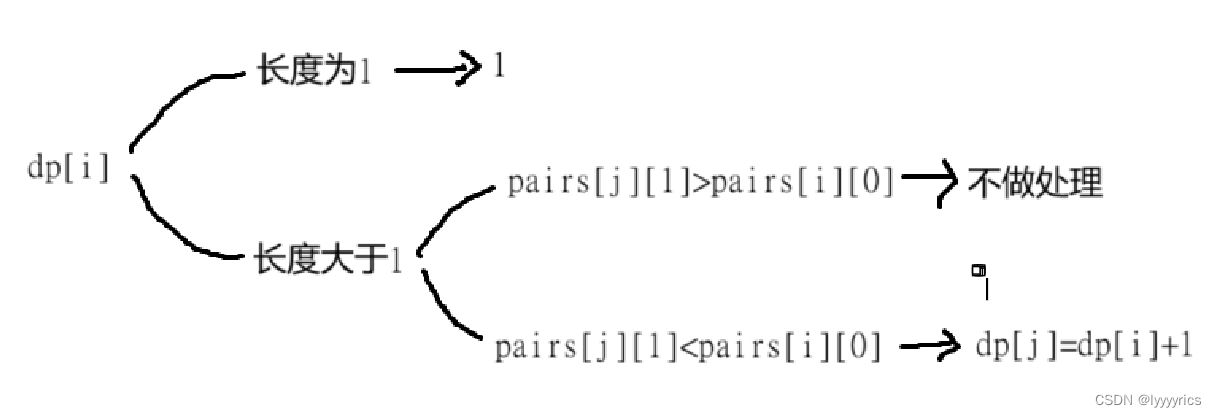
代碼展示：

class Solution {
public:int findLongestChain(vector<vector<int>>& pairs) {sort(pairs.begin(), pairs.end());int n = pairs.size();vector<int> dp(n, 1);int ret = 1;for (int i = 1;i < n;i++){for (int j = i - 1;j >= 0;j--){if (pairs[j][1] < pairs[i][0]){dp[i] = max(dp[j] + 1, dp[i]);}ret = max(dp[i], ret);}}return ret;}
};

運行結果：

5.最長定差子序列

題目鏈接
題目：

樣例 輸出和輸入：

這道題給定一個difference，讓我們求出數組中的差為difference的最長的子序列的長度
算法原理：
狀態表示：dp[i]表示以i位置為結尾的所有子序列中的最長的等差子序列，且差值是difference。
狀態轉移方程：首先我們可以分析一下，我們可以選擇從0位置開始遍歷尋找和i位置之差是difference的數，這里的dp表其實我們可以借助hash表來充當，因為每次我們都得去前面找和i位置差值是difference的數，所以這里hash表既可以充當dp表，也可以將前一個位置和當前位置的差值是difference的數存起來。
這里的狀態轉移方程：hash[arr[i]] = hash[arr[i] - difference] + 1這里如果沒有在hash表中找到前一個位置差值是difference值的數，則hash[arr[i] - difference]就是0，所以也免去了這種情況，由于我們找的是離i位置最近的前一個位置，這里也可以用hash表解決，因為，我們是從左到右遍歷的，這就使得后一個位置每次都是覆蓋了前一個位置的值，每次都是最新的狀態值。

代碼展示：

class Solution {
public:int longestSubsequence(vector<int>& arr, int difference) {unordered_map<int, int> hash;//arr[i]----dp[i]hash[arr[0]] = 1;int ret = 1;for (int i = 1;i < arr.size();i++){//需要的最后一個b的值，這個hash能保證，因為從左到右遍歷，前面的值已經被覆蓋了hash[arr[i]] = hash[arr[i] - difference] + 1;ret = max(ret, hash[arr[i]]);}return ret;}
};

運行結果：

總結

通過本文對子序列問題的探討，我們深入理解了動態規劃在解決此類問題中的重要性。無論是經典的最長公共子序列（LCS）問題，還是最長遞增子序列（LIS）問題，動態規劃都展示了其強大的解題能力。通過將問題分解為更小的子問題，并記錄這些子問題的解，我們能夠高效地找到最優解，避免重復計算。

此外，我們還見識了動態規劃解決子序列問題的多種變體及其實際應用。這不僅拓寬了我們對算法設計的視野，也提升了我們在面對復雜問題時的解決能力。子序列問題不僅在理論上具有重要意義，也在現實世界中的許多領域，如生物信息學、文本處理和數據分析中有著廣泛的應用。

希望通過本文的講解，讀者能對動態規劃在子序列問題中的應用有更深的理解，并能將這些技術應用于實際編程中，解決更多實際問題。動態規劃的學習不僅僅局限于特定問題，更是培養一種思維方式，一種解決復雜問題的系統方法。愿大家在未來的算法學習和應用中繼續精進，取得更大的進步。