寫在前面: 部分來自孫寶(@Steven24)的博客,表示感謝。
認識
什么是Splay
就是BST的一種,整體效率是很高的,均攤的次數是O(logn)級別的。
基本操作就是把節點旋轉到BST的root,從而改善BST的平衡性,但是很多人會在旋轉中轉暈
建議找個動圖看看,或是上B站找個幾分鐘的視頻看看就理解了。
燒烤
如何可以把一個節點旋轉到BST的root的地方,這是Splay的核心,為了完成這個操作,我們主要是需要分成兩步:
1.每旋轉一次,就使得我們的目標節點x的層次上升一層,最后到達root層
2.在旋轉完后,BST的平衡性被破壞了,這是毋庸置疑的,所以我們需要進行一系列的調整,使這棵BST重新回到平衡狀態
顯然,如果只考慮1,那么使用Treap樹的旋轉法即可,每次x與x的父親交換位置(x上升一層)。可Treap樹的這種“單旋”并不能減少BST的層數。
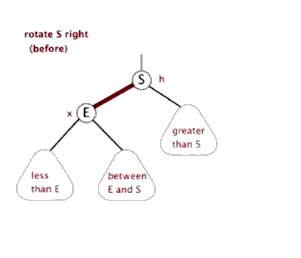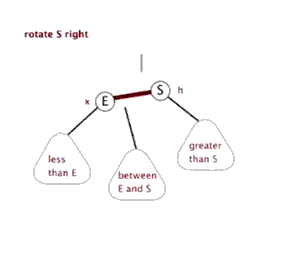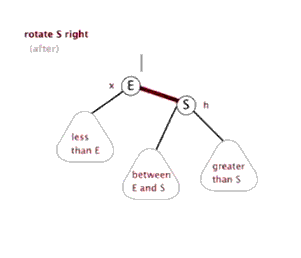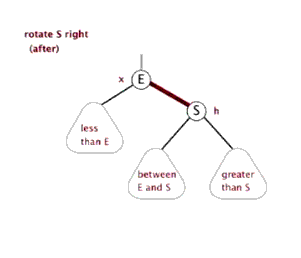
所以我們就升級一下,再拉來一個更能打的,祖父節點,讓這三代人一起轉。
Splay旋轉
#define left 0,right 1
這個就是LL,RR,LR,RL四個Splay的基本模型
網上有很多
自己看吧
我推薦這個,因為我就是看著他弄懂的基礎知識
Splay四種模型
Splay操作
由于支持單點旋轉改變平衡因子的特性Splay常用于處理區間分裂和合并問題。
例如:一個常見的區間操作,修改或查詢區間[L,R],用Splay樹就很容易實現:先把L-1旋轉到根,然后把節點R+1旋轉到L-1的右子樹上,此時,L+1的左子樹就是區間[L,R]。
1.旋轉:
rotate(x)對x點進行一次旋轉,若x是一個右兒子,左旋,反之亦反之。
Splay Rotate
void rotate(int x)//單旋一次
{int f=t[x].fa;//f:父親int g=t[f].fa;//g:祖父int son=get(x);if(son==1)//x是左兒子,右旋{t[f].rs=t[x].ls;if(t[f].rs){t[t[f].rs].fa=f;}}else//x是右兒子,左旋{t[f].ls=t[x].rs;if(t[f].ls){t[t[f].ls].fa=f;}}t[f].fa=x;//x旋為f的父節點if(son==1)//左旋,f變為x的左兒子{t[x].ls=f;}else//右旋,f變為x的右兒子{t[x].rs=f;}t[x].fa=g;//x現在是祖父的兒子if(g)//更新祖父的兒子{if(t[g].rs==f){t[g].rs=x;}else{t[g].ls=x;}}Update(f);Update(x);
}Splay(int x,int goal),把節點x旋轉到goal位置。goal=0表示把x旋轉到根,x是新的根。goal≠0表示把x旋轉為goal的兒子。
Splay Rotate Destiny
?void Splay(int x,int goal)
{if(goal==0){root=x;}while(1){int f=t[x].fa;//一次處理x,f,g三個節點int g=t[f].fa;if(f==goal){break;}if(g!=goal)//有祖父,分為一字旋和之字旋兩種情況{if(get(x)==get(f))//一字旋,先旋轉f,g{rotate(f);}else//之字旋,直接旋轉x{rotate(x);}}rotate(x);}Update(x);
} 2.分裂和合并:
Insert()、Del()函數中包含了分裂與合并,詳情見代碼注釋。利用Splay函數實現分裂與合并,編碼很簡單。
Splay Insert and Delete
?void Insert(int L,int len)//插入一段區間
{int x=kth(root,L);//x為第L個數的位置,y為第L+1個數的位置int y=kth(root,L+1);Splay(x,0);//分裂Splay(y,x);//先把x旋轉到根,然后把y旋轉到x的兒子,且y的兒子為空t[y].ls=build(1,len,y);//合并:建一棵樹,掛到y的左兒子上Update(y);Update(x);
}
void Del(int L,int R)//刪除區間[L+1,R]
{int x=kth(root,L);int y=kth(root,R+1);Splay(x,0);//y是x的右兒子,y的左兒子是待刪除的區間Splay(y,x);t[y].ls=0;//剪短左子樹,等于直接刪除,這里為了簡單,沒有釋放空間Update(y);Update(x);
}3.查詢:
Splay Find
?int kth(int x) { //查詢排名為x的數 int now = root;while (1) {if (siz[son[now][0]] >= x) now = son[now][0]; //查過頭了else if (siz[son[now][0]] + cnt[now] >= x) return val[now]; //正好查到else {x -= (siz[son[now][0]] + cnt[now]);now = son[now][1]; //沒查夠 } }
}Splay Rank
?int rank(int x) { //查詢x的排名 int now = root, ans = 0;while (1) {if (!now) return ans + 1; //樹中不存在這個數 那就是目前查到比它小的數的數目+1if (val[now] > x) now = son[now][0]; //要查的數比now節點的數小 說明在左子樹else if (val[now] == x) {ans += siz[son[now][0]]; //比它小的數的數目splay(now);return ans + 1; } else { //要查的數在左子樹 ans += siz[son[now][0]] + cnt[now]; //此時當前節點和左子樹所有數都比它小 now = son[now][1];}}
}Splay Find pre/nxt
?int findpre() { //查詢根節點的前驅對應的結點編號 int now = son[root][0]; //首先進入左子樹 因為左子樹的所有數都比它小 while (son[now][1]) now = son[now][1]; //然后一直往大的走 找最大的return now;
} int findnxt() { //跟上面同理 int now = son[root][1];while (son[now][0]) now = son[now][0];return now;
}···else if (opt == 5) {splay.insert(x); //把x先旋到根節點 而且一定要插入而不是直接旋 防止樹上本來就沒有xprintf("%d\n", splay.val[splay.findpre()]);splay.del(x); //用完刪掉
} else {splay.insert(x); //同上 printf("%d\n", splay.val[splay.findnxt()]);splay.del(x);
}注意
(感謝孫寶)
所以 splay 容易寫掛的原因找到了 要是哪個 splay 和 maintain 忘寫了就寄了
那么怎么記住到底哪要寫哪不用寫呢
對于 maintain 很簡單 改了啥就把它自己 maintain 一下 再把父親(如果有)也 maintain 一下
對于 splay 實際上我們使用這個函數的同時如果要實現提根的功能 那就寫
比如 insert 我們查詢前驅后繼需要使用它并且把插入的數旋到根 所以要寫
比如 rank 我們就是要用它把權值為 x 的結點旋到根節點 所以要寫
再比如 del 呃這個你肯定不能忘
如果還記不住怎么辦呢
首先要明確 splay 是復雜度的保證 寫少了復雜度就會假
但是寫幾個肯定是沒事的
maintain 也是 如果該更新的沒更新肯定就寄了
但是把沒必要更新的也更新了問題就不大
所以實在不行這倆就是能寫就寫
當然這么干常數就又會變大 所以最好還是記一下上面那個




- 需要自定義著色器)




)




Sync.Map)
- 邏輯回歸)

:大數據可視化綜合實訓)

