注意咯，如果說前期的文章隨便看看就行，但從這篇往后的內容，則需要君略微動動brain了。當然，后續的文章如果感覺吃力的話，可以看看本專欄序號比較小的文章，可能會對你開卷有益。

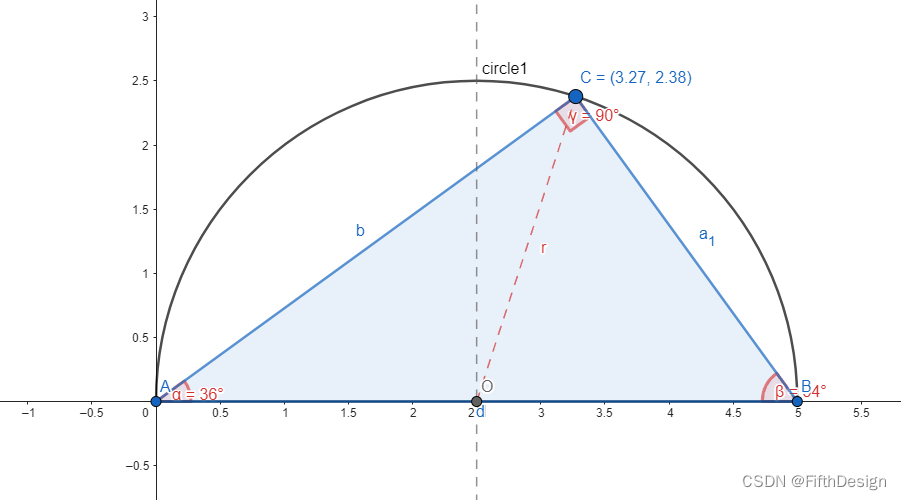
若A, B, C是圓周上的三點，且AC是該圓的直徑，那么∠ABC必然為直角。或者說，直徑所對的圓周角是直角。——泰勒斯定理

一、驗證展示（截圖）

二、涉及內容

1. 根據兩點繪制半圓；
2. 繪制中垂線；
3. 獲取交點；
4. 動點在指定曲線上移動（難點）；
5. 標注角度；
6. 動畫開始。

三、做圖步驟

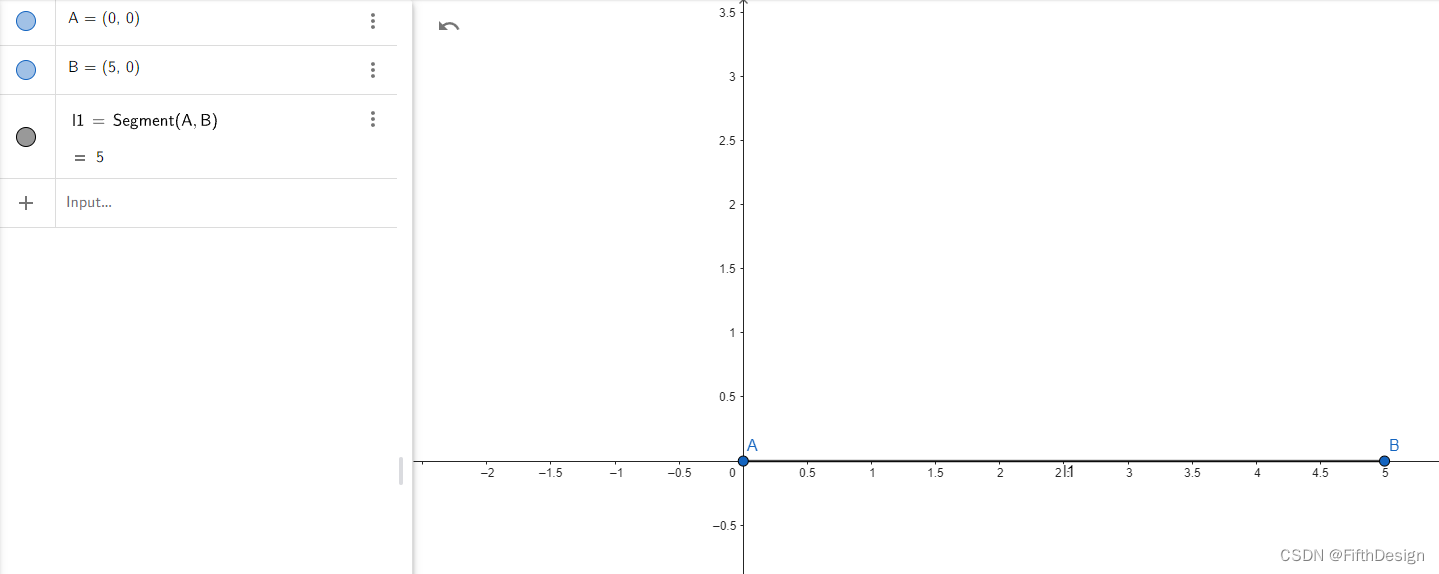
1. 繪制兩點并建立線段；

A=(0,0)
B=(5,0)
l1=Segment(A,B)

2. 根據兩點繪制半圓；

circle1: Semicircle(A,B)

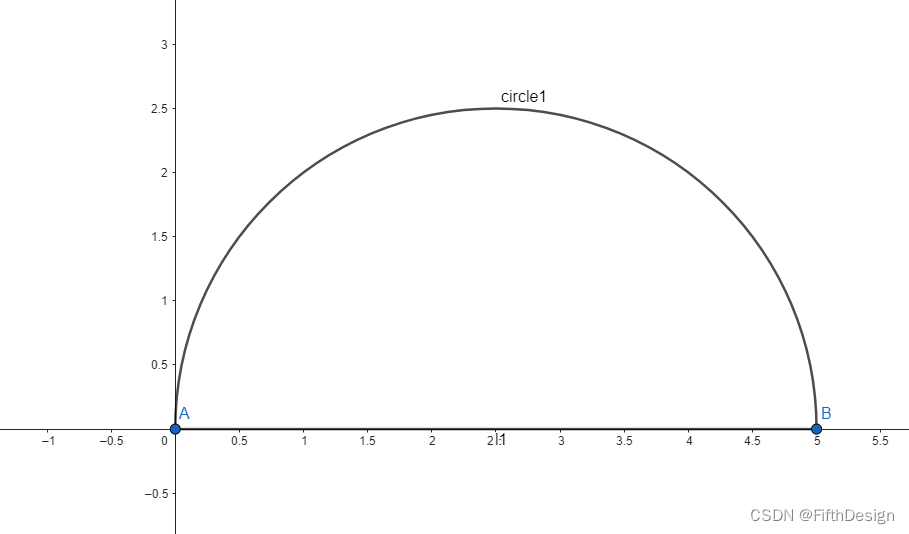
這里是一個新的指令，需要記一下，圓是circle，半圓就是semicircle

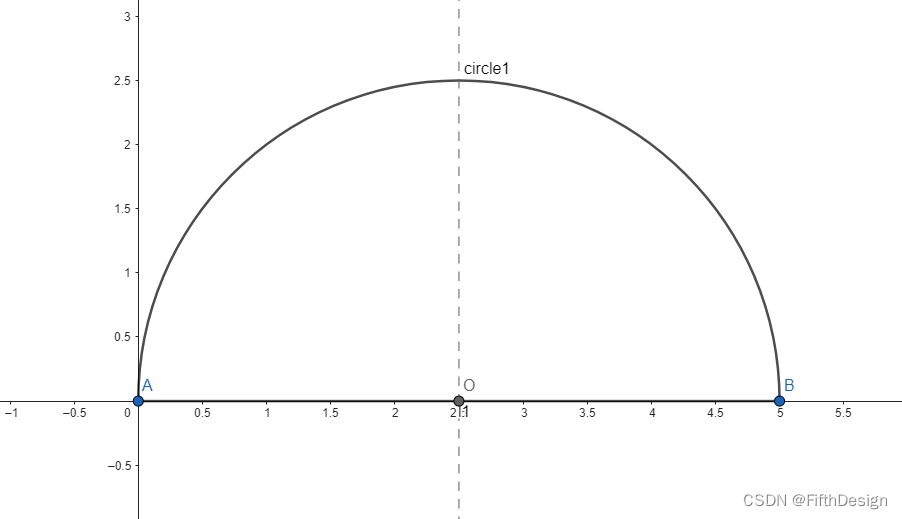
3. 建立中垂線獲取點O；

l2: PerpendicularBisector(l1)
O=Intersect(l1,l2)

4. 建立動點并讓其在半圓上移動；

（1）建立滑動條

s1=0.53

注意，這里的滑動條就有講究了，將會表示點在曲線上走過的距離占曲線總長的百分比，因為百分比只有0到1，所以這個滑動條的范圍只能取0到1（我設置的步進值是0.01）（若有其他情況后邊再補充，暫時可以這么理解）

（2）建立動點C

C=Point(circle1,s1)

1. 滑動點C，就可以發現點實在弧線上移動的；
2. 這次建立點的方式很特殊，第一個參數是對象，表示在這個對象上移動，第二個參數是百分比，表示移動完成了多少（這種建點的方式需要牢記，后邊很常用）；
3. 注意，如果自己的點的數值像我下邊這樣（2.2647292167037……，……），需要在設置界面保留一下小數，我保留的是兩位小數：

5. 繪制三角形ABC；

t=Polygon(A,B,C)

警惕：繪制多邊形的時候點與點之間怎么個順序不重要，有順序很重要。

6. 繪制半圓的半徑；

r=Segment(O,C)

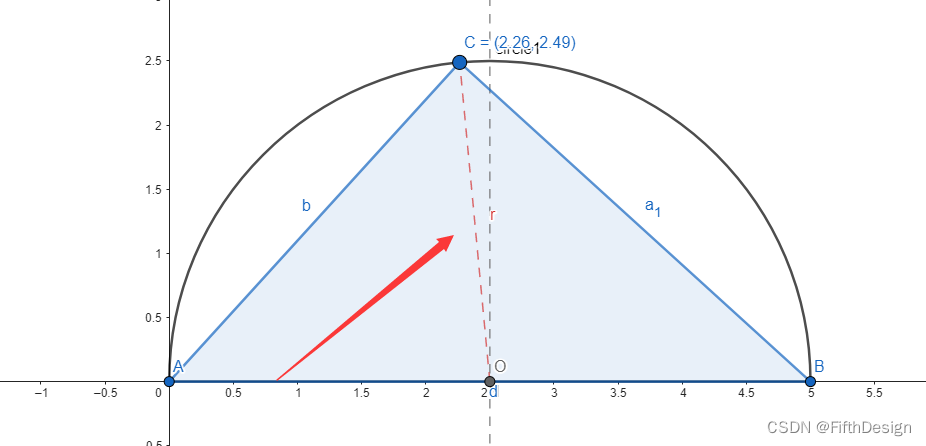
7. 標注圓的內角；

α=Angle(B,A,C)
β=Angle(C,B,A)
γ=Angle(A,C,B)

為了方便看清，可以設置一下格式，因為比較簡單，所以就沒有單獨拿出來講。

8. 動畫驗證泰勒斯定理；

點擊進度條旁邊的播放按鈕，根據動畫可以驗證：

若A, B, C是圓周上的三點，且AC是該圓的直徑，那么∠ABC必然為直角。或者說，直徑所對的圓周角是直角。——泰勒斯定理

注意，如果還不會GeoGebra怎么導出gif動畫，可以看本專欄的往期文章：《006-GeoGebra基礎篇-GeoGebra劃定區域導出gif動圖》

四、正確性檢查

選中一點拖動一下，避免出現有散點、散線，說明肯定有步驟不太對，就需要檢查一下了。

五、文章最后

若有任何問題都可以在這個鋪子問客服，也會有資源相送，GeoGebra、PPT、平面動畫、3D動畫等各種技術都可以，祝好！