【第五節】C/C++數據結構之圖

一、圖的基本概念

1.1 圖的定義

1.2 圖的其他術語概念

二、圖的存儲結構

2.1 鄰接矩陣

2.2 鄰接表

三、圖的遍歷

3.1 廣度優先遍歷

3.2 深度優先遍歷

四、最小生成樹

4.1 最小生成樹獲取策略

4.2 Kruskal算法

4.3 Prim算法

五、最短路徑問題

5.1 Dijkstra算法

5.2 Bellman-Ford算法

5.3 Floyd-Warshall算法

六、AOV網絡和AOE網絡

6.1 AOV網絡（Activity On Vertex Network）

6.2 AOE網絡（Activity On Edge Network）

6.3 異同點

七、總結

一、圖的基本概念

1.1 圖的定義

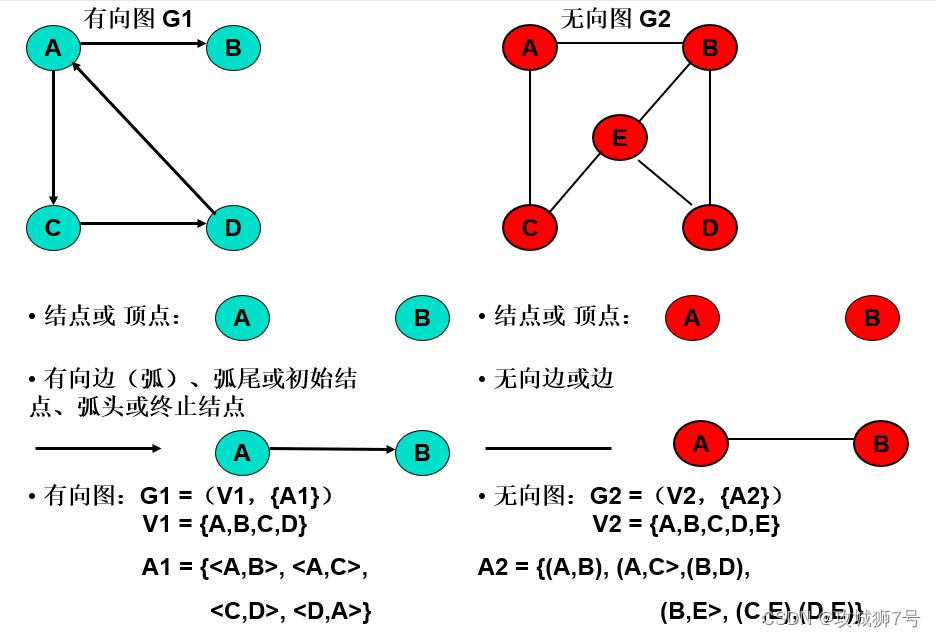
????????數據結構中圖的定義是：圖（Graph）是由頂點的有窮非空集合和頂點之間邊的集合組成，通常表示為G(V, E)，其中G表示一個圖，V表示頂點的集合（也稱為頂集或Vertices Set），E表示頂點之間邊的集合（也稱為邊集或Edges Set）。

頂點（Vertex）：圖中的數據元素，也稱為節點或點。
邊（Edge）：頂點之間的邏輯關系，用來表示兩個頂點之間的連接關系。在無向圖中，邊沒有方向，用無序偶對(u, v)來表示；在有向圖中，邊具有方向，用有序偶<u, v>來表示，其中u稱為弧尾(Tail)，v稱為弧頭(Head)。

此外，圖還有以下一些相關的概念和定義：

有向圖（Directed Graph）：圖中任意兩個頂點之間的邊都是有向邊。
無向圖（Undirected Graph）：圖中任意兩個頂點之間的邊都是無向邊。
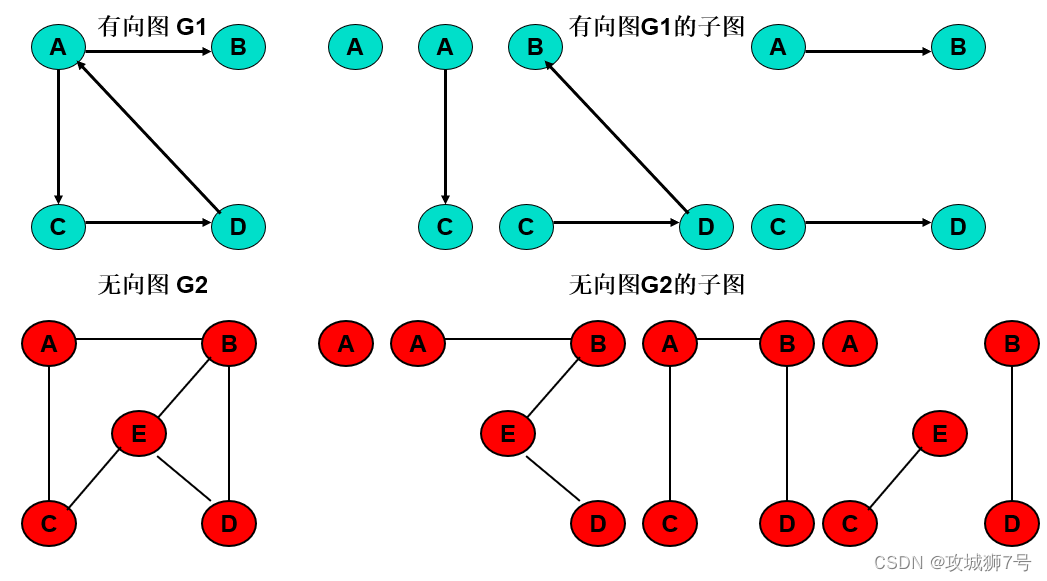
階（Order）：圖G中點集V的大小稱作圖G的階。
子圖（Sub-Graph）：當圖G'=(V', E')，其中V'包含于V，E'包含于E，則G'稱作圖G=(V, E)的子圖。
度（Degree）：一個頂點的度是指與該頂點相關聯的邊的條數。在無向圖中，頂點的度就是其邊的數量；在有向圖中，頂點的度分為入度和出度，入度是指以其為終點的邊數，出度是指以該頂點為起點的邊數。

1.2 圖的其他術語概念

完全圖：在無向圖中，假設頂點數量為N，那么有N*(N-1)/2,條邊，即任意兩個頂點之間都有邊相連，那么就稱其為無向完全圖。在有向圖中，任意兩個頂點之間都有兩條指向相反的連接線，即有N個頂點的有向圖有N*(N-1)條邊，稱這樣的圖結構為有向完全圖。

鄰接頂點：在無向圖中，若存在邊(A,B)，則頂點A與頂點B互為鄰接頂點。在有向圖中，若存在邊<A,B>，則稱頂點A鄰接到頂點B，而頂點B鄰接自頂點A，表示A指向B的連接關系。

頂點的度：頂點的度定義為與該頂點相連的邊的數量，記作deg(V)，代表頂點V的度。在有向圖中，頂點V的度為其入度與出度之和。出度是以V為起點的邊的數量，記作outdeg(V)；入度是以V為終點的邊的數量，記作indeg(V)。因此，deg(V) = outdeg(V) + indeg(V)。在無向圖中，由于邊無方向，頂點的度等同于其出度和入度，即deg(V) = outdeg(V) = indeg(V)。

路徑：在圖G = { V, E }中，如果從頂點vi出發，能夠經過一系列頂點到達頂點vj，則這一系列頂點構成的序列稱為從頂點vi到頂點vj的路徑。

路徑長度：對于無權圖，路徑長度指的是從源頂點到目標頂點所經過的邊的數量。而在帶權圖中，路徑長度則是源頂點到目標頂點所經過的邊的權值之和。權值通常作為邊的附加信息，用于表示某種特定的度量或屬性。

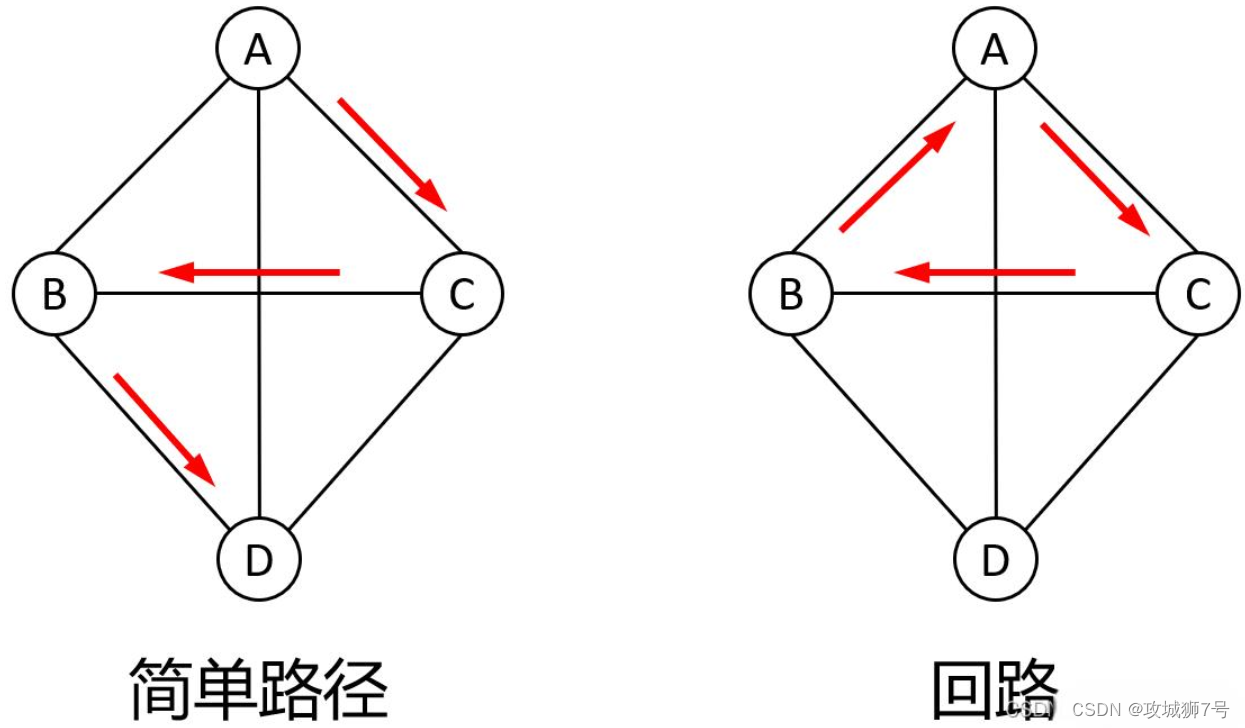
簡單路徑與回路：假設頂點v1和vm相連，路徑v1, v2, ... , vm沒有重復的頂點，那么稱v1, v2, ... , vm為簡單路徑，如果v1,v2, ..., v1，路徑從起始點開始又回到了起始點，那么就是回路。

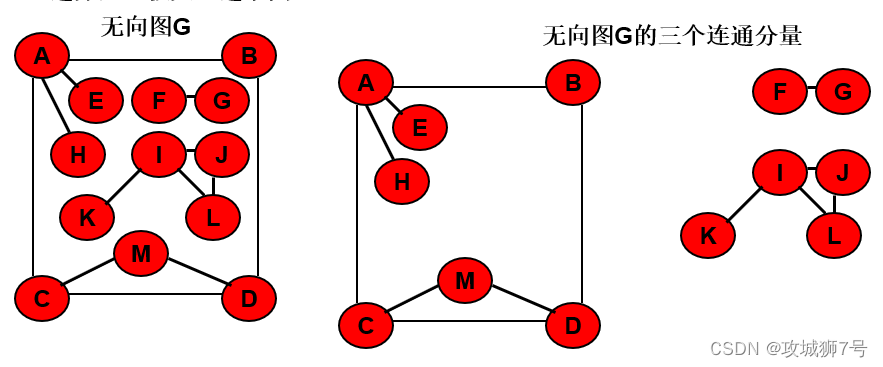
無向圖的連通性

? 路徑：在無向圖 G=(V,{E}) 中由頂點 v 至 v‘’ 的頂點序列。

? 回路或環：第一個頂點和最后一個頂點相同的路徑。

? 簡單回路或簡單環：除第一個頂點和最后一個頂點之外，其余頂點不重復出現的回路。

? 連通：頂點 v 至 v‘’ 之間有路徑存在

? 連通圖：無向圖圖 G 的任意兩點之間都是連通的，則稱 G 是連通圖。

? 連通分量：極大連通子圖

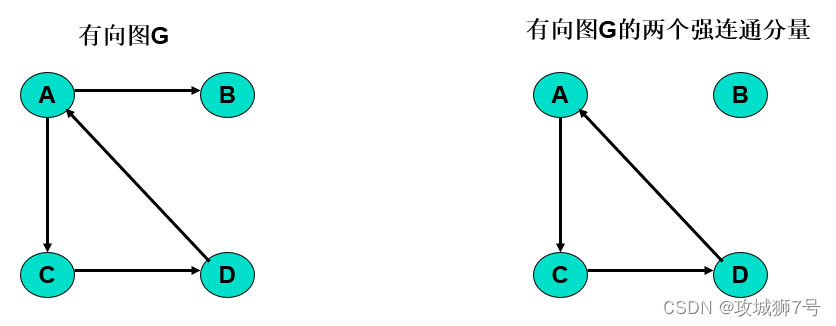
有向圖的連通性

? 路徑：在有向圖 G=(V,{E}) 中由頂點 v 經有向邊至 v‘’ 的頂點序列。

? 回路或環：第一個頂點和最后一個頂點相同的路徑。

? 簡單回路或簡單環：除第一個頂點和最后一個頂點之外，其余頂點不重復出現的回路。

? 連通：頂點 v 至 v‘’ 之間有路徑存在

? 強連通圖：有向圖圖 G 的任意兩點之間都是連通的，則稱 G 是強連通圖。

? 強連通分量：極大連通子圖

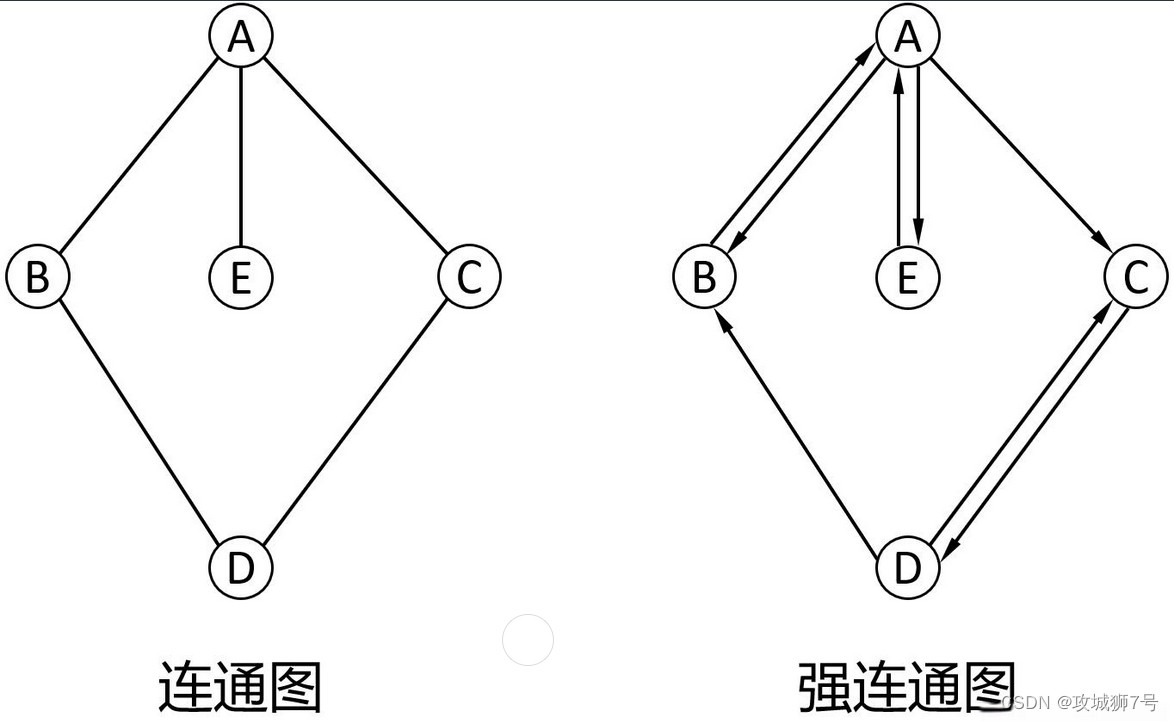
最小生成樹：對于連通圖，能夠將每個頂點連接在一起的最小連通子圖，稱為最小生成樹，對于有N個頂點的連通圖，其最小生成樹應該有N-1條邊。

二、圖的存儲結構

圖的存儲結構主要有兩種：鄰接矩陣（Adjacency Matrix）和鄰接表（Adjacency List）。

2.1 鄰接矩陣

定義：鄰接矩陣使用一個二維數組來存儲圖中頂點間的關系（邊或弧）。對于無向圖，鄰接矩陣是對稱的；對于有向圖，鄰接矩陣可能不是對稱的。
特點：
- 無向圖的鄰接矩陣對稱且唯一。
- 有向圖的鄰接矩陣的第i行非零元素個數為第i個頂點的出度；第j列非零元素個數為第j個頂點的入度1。
- 對于帶權圖，鄰接矩陣的元素可以用來存儲權值；如果兩結點無連接，可以用無窮大（∞）表示。
適用場景：稠密圖（即邊數較多的圖）更適合用鄰接矩陣存儲。

鄰接矩陣的優缺點：鄰接矩陣能夠快速查找兩個頂點是否直接相連，但是如果邊較少的時候，鄰接矩陣中會有大量的 $\oe$ $\infty$ 浪費空間，且使用鄰接矩陣不容易求得兩個頂點之間的路徑。

代碼實現

#include <iostream>
#include <vector>
#include <unordered_map>
#include <optional>
#include <stdexcept>namespace Matrix
{// Graph 類模板定義// V - 頂點類型// W - 權重類型// MAX_W - 權重的最大值，默認為 INT_MAX// Direction - 是否為有向圖，默認為無向圖 (false)template<class V, class W, W MAX_W = INT_MAX, bool Direction = false>class Graph{public:// 構造函數，初始化圖的頂點// arr - 頂點數組// size - 頂點數組的大小Graph(const V* arr, size_t size){for (size_t i = 0; i < size; ++i){_vertex.push_back(arr[i]);_valIndexMap[arr[i]] = i;}// 初始化鄰接矩陣，所有權重設為 MAX_W_edges.resize(size, std::vector<W>(size, MAX_W));}// 獲取頂點值對應的索引// val - 頂點值// 返回頂點值對應的索引，如果頂點不存在則返回 std::nulloptstd::optional<size_t> GetIndex(const V& val) const{auto pos = _valIndexMap.find(val);if (pos != _valIndexMap.end()){return pos->second;}return std::nullopt; // 頂點不存在}// 添加邊到圖中// src - 源頂點// dst - 目標頂點// w - 邊的權重void AddEdge(const V& src, const V& dst, const W& w){auto srci = GetIndex(src);auto dsti = GetIndex(dst);// 檢查頂點是否存在if (!srci || !dsti){throw std::runtime_error("One or both vertices not found in the graph.");}// 添加邊_edges[*srci][*dsti] = w;// 如果是無向圖，還需要添加反向邊if (!Direction){_edges[*dsti][*srci] = w;}}// 打印鄰接矩陣void Print() const{size_t n = _vertex.size();for (size_t i = 0; i < n; ++i){for (size_t j = 0; j < n; ++j){// 如果權重為 MAX_W，則打印 '*' 表示無邊if (_edges[i][j] == MAX_W) std::cout << "*  ";else std::cout << _edges[i][j] << "  ";}std::cout << std::endl;}}private:std::vector<V> _vertex; // 頂點數組std::unordered_map<V, size_t> _valIndexMap; // 頂點到索引的映射std::vector<std::vector<W>> _edges; // 鄰接矩陣};
}

????????整個類的設計側重于使用鄰接矩陣來表示圖，這在頂點數量較少時很有效，但對于邊數遠少于頂點對數的稀疏圖，這種表示方法可能會浪費大量內存。此外，類模板的靈活性允許用戶定義頂點和邊權重的數據類型，并選擇圖的方向性。

2.2 鄰接表

定義：鄰接表是一種順序分配和鏈式分配相結合的存儲結構。如果表頭結點所對應的頂點存在相鄰頂點，則把相鄰頂點依次存放于表頭結點所指向的單向鏈表中。
特點：
- 鄰接表是為了節省存儲空間而引入的，對于稀疏圖（即邊數較少的圖），相對于鄰接矩陣，無需耗費大量存儲空間。
- 對于有向圖，還有逆鄰接表的概念，逆鄰接表可以得到圖的入度。
適用場景：稀疏圖更適合用鄰接表存儲

代碼示例

#include <iostream>
#include <vector>
#include <unordered_map>
#include <optional>
#include <stdexcept>namespace LinkTable
{// Edge 結構體代表圖中的邊template<class W>struct Edge{size_t _dsti;  // 目標頂點在數組中的下標W _w;          // 邊的權重Edge* _next;   // 鏈表中的下一條邊// 構造函數初始化邊Edge(size_t dsti, const W& w): _dsti(dsti), _w(w), _next(nullptr){ }};// Graph 類模板定義template<class V, class W, W MAX_W = INT_MAX, bool Direction = false>class Graph{public:typedef Edge<W> EdgeType;// 構造函數，初始化圖的頂點Graph(const V* arr, size_t size){for (size_t i = 0; i < size; ++i){_vertex.emplace_back(arr[i]);_valIndexMap[arr[i]] = i;}// 初始化鄰接表_edges.resize(size, nullptr);}// 析構函數，負責釋放所有動態分配的邊~Graph(){for (auto& edge : _edges){while (edge){EdgeType* temp = edge;edge = edge->_next;delete temp;}}}// 獲取頂點值對應的索引std::optional<size_t> GetIndex(const V& val) const{auto pos = _valIndexMap.find(val);if (pos != _valIndexMap.end()){return pos->second;}return std::nullopt; // 頂點不存在}// 添加邊到圖中void AddEdge(const V& src, const V& dst, const W& w){auto srci = GetIndex(src);auto dsti = GetIndex(dst);if (!srci || !dsti){throw std::runtime_error("One or both vertices not found in the graph.");}// 添加邊從src到dstEdgeType* edge1 = new EdgeType(*dsti, w);edge1->_next = _edges[*srci];_edges[*srci] = edge1;// 如果是無向圖，添加邊從dst到srcif (!Direction){EdgeType* edge2 = new EdgeType(*srci, w);edge2->_next = _edges[*dsti];_edges[*dsti] = edge2;}}// 打印鄰接表void Print() const{size_t n = _edges.size();for (size_t i = 0; i < n; ++i){std::cout << _vertex[i] << ":";EdgeType* cur = _edges[i];while (cur){std::cout << " -> [" << _vertex[cur->_dsti] << ":" << cur->_w << "]";cur = cur->_next;}std::cout << " -> nullptr" << std::endl;}}private:std::vector<V> _vertex;   // 頂點數組std::unordered_map<V, size_t> _valIndexMap;   // 頂點到索引的映射std::vector<EdgeType*> _edges;   // 鄰接表};
}

????????這個 Graph 類的設計使用鄰接表來表示圖，這比鄰接矩陣更適合表示稀疏圖，因為它可以減少內存占用，并可能提高遍歷邊的效率。與之前的鄰接矩陣實現相比，這種實現方式在處理大量頂點和邊時通常更高效。

三、圖的遍歷

3.1 廣度優先遍歷

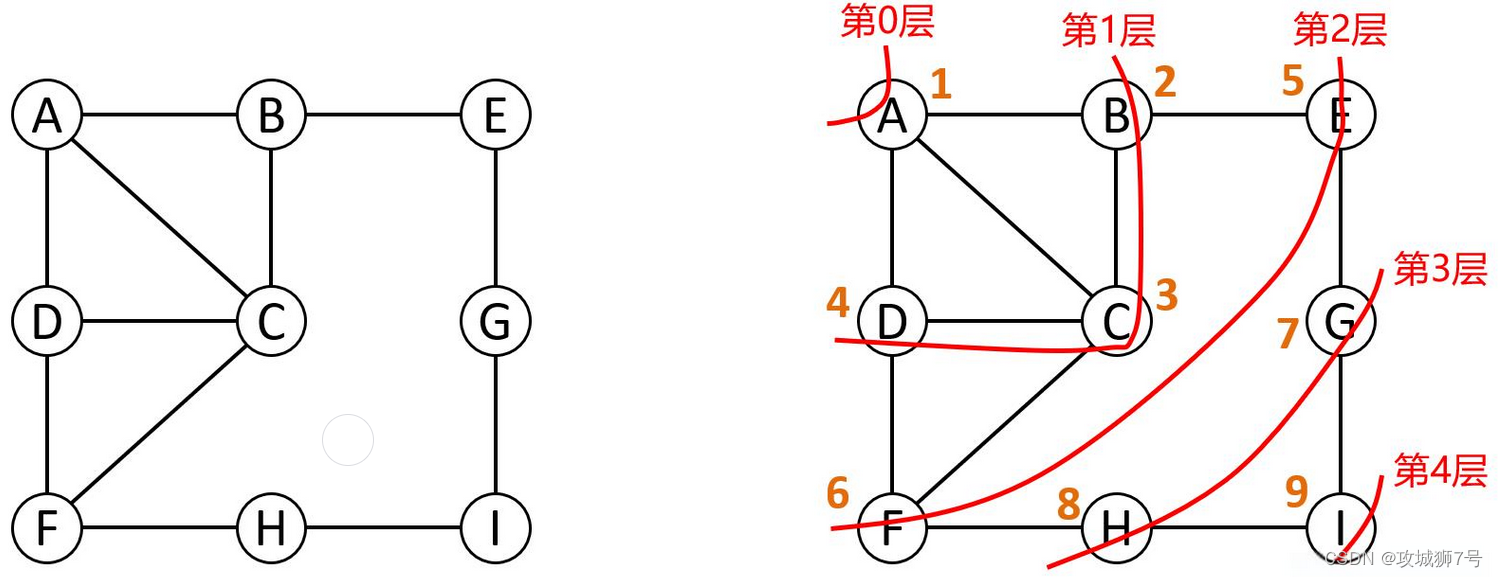
????????廣度優先遍歷（Breadth-First Search, BFS）是一種用于遍歷或搜索樹或圖的算法。這個算法從圖的某一頂點（源頂點）開始，首先訪問起始頂點，然后訪問其所有相鄰頂點，接著再訪問這些相鄰頂點的未訪問過的相鄰頂點，依此類推，直到所有頂點都被訪問為止。

廣度優先遍歷通常使用隊列（Queue）來實現。下面是廣度優先遍歷的基本步驟：

創建一個隊列Q，并將起始頂點v加入隊列Q。
創建一個集合visited來記錄已被訪問的頂點，并將v標記為已訪問。
當隊列Q非空時，重復以下步驟：
a. 從隊列Q中取出一個頂點u。
b. 訪問頂點u。
c. 對于u的每一個未被訪問過的相鄰頂點v，將v加入隊列Q，并標記v為已訪問。
當隊列Q為空時，算法結束。此時，所有可達的頂點（從起始頂點開始）都已被訪問。

示例代碼：

#include <iostream>
#include <vector>
#include <queue>
#include <unordered_map>
#include <optional>// ...（其他代碼保持不變）...template<class V, class W, W MAX_W = INT_MAX, bool Direction = false>
class Graph
{// ...（其他成員和方法保持不變）...// 圖的廣度優先遍歷，src為遍歷起點void BFS(const V& src){std::optional<size_t> srcIndexOpt = GetIndex(src);  // 獲取起點的索引if (!srcIndexOpt.has_value()) {throw std::runtime_error("The source vertex does not exist in the graph.");}size_t srcIndex = srcIndexOpt.value();  // 起點索引size_t n = _vertex.size();  // 頂點個數std::vector<bool> visited(n, false);  // 記錄每個頂點是否已訪問std::queue<size_t> q;  // 隊列，用于存儲將要訪問的頂點索引q.push(srcIndex);  // 將起點索引入隊visited[srcIndex] = true;  // 標記起點為已訪問size_t level = 0;  // 當前層級// 當隊列不為空時，循環執行while (!q.empty()){size_t levelSize = q.size();  // 當前層的頂點數量std::cout << "第 " << level << " 層：";for (size_t i = 0; i < levelSize; ++i){size_t currentVertexIndex = q.front();  // 獲取隊列前端的頂點索引q.pop();  // 將當前頂點索引從隊列中移除std::cout << _vertex[currentVertexIndex] << " ";  // 打印當前頂點// 遍歷當前頂點的所有鄰接邊for (EdgeType* edge = _edges[currentVertexIndex]; edge != nullptr; edge = edge->_next){size_t adjacentIndex = edge->_dsti;  // 獲取鄰接頂點的索引// 如果鄰接頂點未被訪問，則將其加入隊列if (!visited[adjacentIndex]){visited[adjacentIndex] = true;  // 標記鄰接頂點為已訪問q.push(adjacentIndex);  // 將鄰接頂點索引入隊}}}std::cout << std::endl;level++;  // 層級加一}}
};// ...（其他代碼保持不變）...

3.2 深度優先遍歷

????????圖的深度優先遍歷（Depth-First Search, DFS）是一種用于遍歷或搜索樹或圖的算法。這個算法會盡可能深地搜索圖的分支。當節點v的所在邊都已被探尋過，搜索將回溯到發現節點v的那條邊的起始節點。這一過程一直進行到已發現從源節點可達的所有節點為止。如果還存在未被發現的節點，則選擇其中一個作為源節點并重復以上過程，整個進程反復進行直到所有節點都被訪問為止。

????????深度優先遍歷通常使用棧（Stack）來實現，但也可以使用遞歸。以下是深度優先遍歷的基本步驟：

創建一個集合visited來記錄已被訪問的頂點。
選擇一個起始頂點v，并將其標記為已訪問。
遞歸地（或使用棧）訪問v的所有未訪問過的相鄰頂點。對于每個這樣的頂點u，如果u未被訪問過，則標記u為已訪問，并遞歸地（或使用棧）訪問u的所有未訪問過的相鄰頂點。
當所有可訪問的頂點都已被訪問時，算法結束。

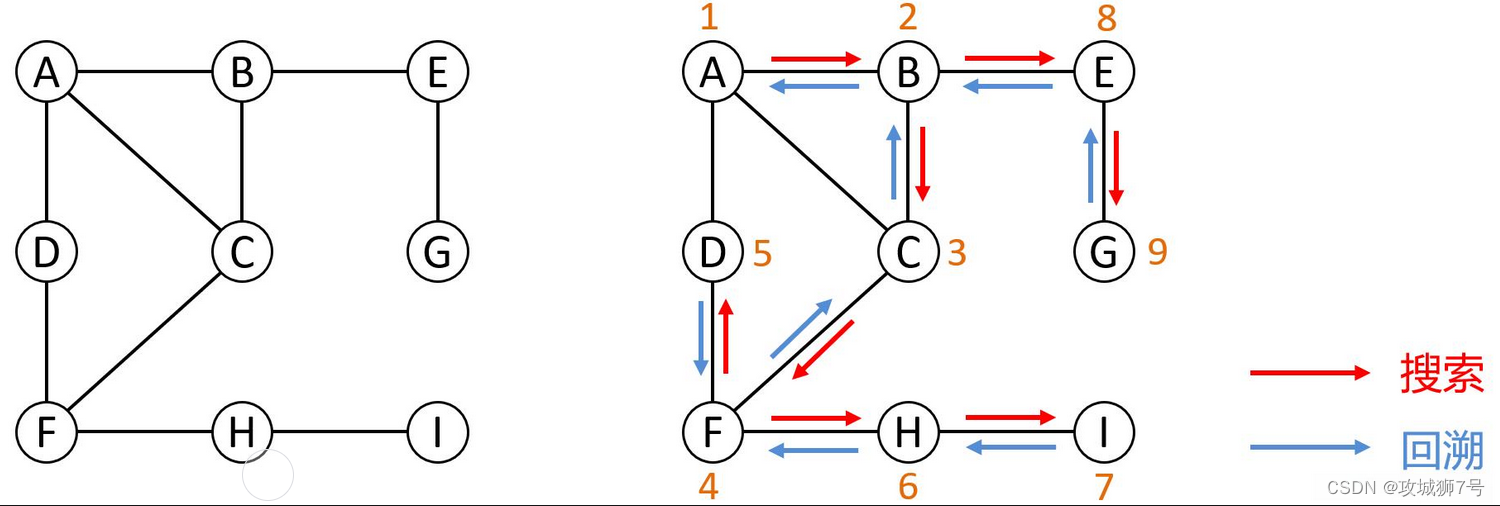
代碼示例：

#include <iostream>
#include <vector>
#include <unordered_map>
#include <optional>// ...（其他代碼保持不變）...template<class V, class W, W MAX_W = INT_MAX, bool Direction = false>
class Graph
{// ...（其他成員和方法保持不變）...// 深度優先遍歷算法子函數// curi為當前遍歷節點的下標，visited為記錄節點是否被遍歷過的數組void _DFS(size_t curi, std::vector<bool>& visited){// 標記當前節點為已訪問visited[curi] = true;// 輸出當前節點std::cout << _vertex[curi] << " ";// 遍歷與當前節點相連的所有節點for (EdgeType* edge = _edges[curi]; edge != nullptr; edge = edge->_next){size_t u = edge->_dsti;  // 獲取相連節點的索引// 如果相連節點未訪問，則遞歸調用DFSif (!visited[u]){_DFS(u, visited);}}}// 深度優先遍歷函數，src為起始點void DFS(const V& src){// 獲取起始點的索引，如果不存在則拋出異常std::optional<size_t> srcIndexOpt = GetIndex(src);if (!srcIndexOpt.has_value()) {throw std::runtime_error("The source vertex does not exist in the graph.");}size_t srcIndex = srcIndexOpt.value();// 初始化訪問標記數組size_t n = _vertex.size();std::vector<bool> visited(n, false);// 從起始點開始執行DFS_DFS(srcIndex, visited);}
};// ...（其他代碼保持不變）...

四、最小生成樹

4.1 最小生成樹獲取策略

????????所謂最小生成樹，是對于無向連通圖的概念，即：路徑權值和最小的、連通的子圖。這就要求最小生成樹滿以下條件：

??? 如果原圖有N個頂點，那么其最小生成樹有N-1條邊。
??? 最小生成樹中的邊不能構成回路。
??? 必須是滿足前兩個條件，邊權值和最小的生成樹。

????????獲取最小生成樹的算法有Kruskal算法(克魯斯卡爾算法)和Prim算法(普里姆算法)，這兩種算法都是采用“貪心”策略，即尋找局部最優解，即：當前圖中滿足一定條件的權值最小的邊。但是要注意，Kruskal算法和Prim算法都是局部貪心算法，能夠取得局部最優解，但是不一定獲取的是全局最優解，它們獲取的結果只能說是非常接近于最小生成樹，而不一定就是最小生成樹。

4.2 Kruskal算法

????????Kruskal算法的思想就是在整個圖的所有邊中，篩選出權值最小的邊，同時在選邊的過程中避免構成環，等到篩選出N-1條邊后，就可以獲取最小生成樹。圖4.1為Kruskal算法的選邊過程，其中紅色加粗的線為被選擇的邊。

Kruskal算法核心：每次都篩選權值最小的、且不構成回路的邊，加入生成樹。

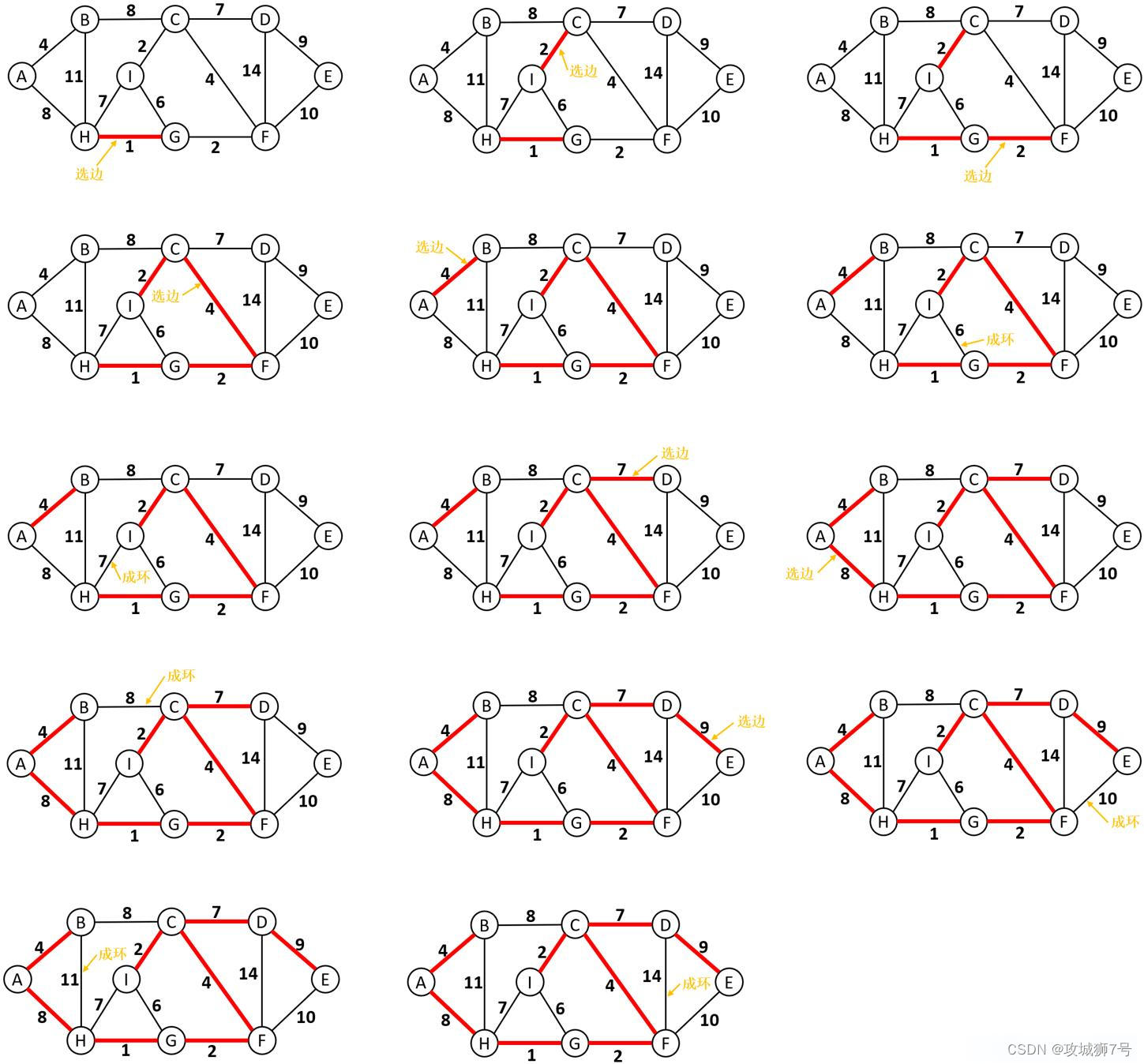
????????通過Kruskal算法獲取最小生成樹需要使用小根堆 + 并查集來輔助進行，其中小根堆負責每次在所有尚未選取的邊中篩選權值最小的邊，并查集用于避免生成回路（環）。需要定義struct Edge類來記錄邊的屬性信息，struct Edge的成員包括起始頂點下標srci、目標頂點下標dsti以及權重w，重載> 運算符，用于比較權重大小。在Kruskal算法的代碼中首先要將所有的邊插入小根堆，每次從堆頂拿出一條邊，使用并查集檢查兩個頂點是否會構成環（屬于同一個集合），如果不會構成環，那么就將這條邊添加到生成樹中去。之后，將此時的srci和dsti歸并到并查集的同一集合中去以避免成環，然后選邊計數器+1，進行權重累加。假設總共有N個頂點，如果選出生成樹有N-1條邊，說明成功獲得了最小生成樹，返回每個邊的權重之和，否則就是獲取最小生成樹失敗，返回MAX_W。

下面代碼為Kruskal算法及其配套被調函數及自定義類型的實現，其中Graph的其余不相關函數省略

#include "UnionFindSet.hpp"
#include <iostream>
#include <vector>
#include <queue>
#include <unordered_map>
#include <algorithm>
#include <cassert>namespace Matrix
{// 自定義類型 -- 頂點與頂點之間的邊template<class W>struct Edge{size_t _srci;   // 源頂點下標size_t _dsti;   // 目標頂點下標W _w;           // 權重// 構造函數Edge(size_t srci, size_t dsti, const W& w): _srci(srci), _dsti(dsti), _w(w){ }// 大于比較運算符重載函數，用于構建小根堆bool operator>(const Edge<W>& w) const{return _w > w._w;}};template<class V, class W, W MAX_W = INT_MAX, bool Direction = false>class Graph{typedef Edge<W> Edge;typedef Graph<V, W, MAX_W, Direction> Self;public:// 強制生成默認構造函數Graph() = default;// ....// 與Kruskal算法不相關的成員函數全部省略// 根據下標添加邊的函數void _AddEdge(size_t srci, size_t dsti, const W& w){_edges[srci][dsti] = w;if (!Direction) // 如果圖是無向的，則需要在鄰接矩陣中添加兩個方向的邊{_edges[dsti][srci] = w;}}// Kruskal算法獲取最小生成樹// 返回值為最小生成樹的權值和，minTree為輸出型參數，用于獲取最小生成樹// 如果無法獲取最小生成樹，那么就返回MAX_WW Kruskal(Self& minTree){// 初始化minTree中的每個成員size_t n = _vertex.size();minTree._vertex = _vertex;minTree._valIndexMap = _valIndexMap;minTree._edges.resize(n, std::vector<W>(n, MAX_W));// 將所有邊的信息（源頂點、目標頂點、權值）插入到小根堆中去std::priority_queue<Edge, std::vector<Edge>, std::greater<Edge>> minHeap;for (size_t i = 0; i < n; ++i){for (size_t j = i + 1; j < n; ++j){if (_edges[i][j] != MAX_W){minHeap.emplace(i, j, _edges[i][j]);}}}UnionFindSet ufs(n);    // 用于避免構成回路的并查集size_t count = 0;       // 計數器，用于統計選取了多少條邊W totalW = W();         // 總權值計數器std::cout << "Kruskal開始選邊：" << std::endl;while (!minHeap.empty() && count < n - 1){// 小根堆堆頂為當前尚未被篩選且權值最小的邊Edge curEdge = minHeap.top();minHeap.pop();// 檢查當前兩個節點是否位于同一并查集的集合中if (!ufs.InSet(curEdge._srci, curEdge._dsti)){std::cout << "[" << _vertex[curEdge._srci] << "->" << _vertex[curEdge._dsti] << "]:" << curEdge._w << std::endl;// 向最小生成樹中添加srci->dsti的邊minTree._AddEdge(curEdge._srci, curEdge._dsti, curEdge._w);// 將srci和dsti歸為同一集合ufs.Union(curEdge._srci, curEdge._dsti);// 選邊計數器+1，權值累加++count;totalW += curEdge._w;}else{std::cout << "構成環  " << "[" << _vertex[curEdge._srci] << "->" << _vertex[curEdge._dsti] << "]:" << curEdge._w << std::endl;}}// 如果選擇了n-1條邊，那么說明獲取了最小生成樹，否則獲取最小生成樹失敗if (count == n - 1) {return totalW;}else {return MAX_W;}}private:std::vector<V> _vertex;    // 存儲頂點值的一維數組std::unordered_map<V, size_t> _valIndexMap;   // 頂點值與其在數組下標中的映射關系std::vector<std::vector<W>> _edges;        // 鄰接矩陣};
}

并查集的實現代碼如下

#pragma once#include <vector>
#include <algorithm>class UnionFindSet {
public:// 構造函數，初始化n個元素的并查集UnionFindSet(size_t n) : _ufs(n, -1) {}// 合并兩個元素所在的集合void Union(int x1, int x2) {int root1 = FindRoot(x1);int root2 = FindRoot(x2);// 如果兩個元素已經在同一個集合中，則無需合并if (root1 == root2)return;// 按秩合并，將秩較小的根節點合并到秩較大的根節點上if (abs(_ufs[root1]) < abs(_ufs[root2]))std::swap(root1, root2);// 更新集合的秩，并將root2的根節點指向root1_ufs[root1] += _ufs[root2];_ufs[root2] = root1;}// 查找元素x的根節點int FindRoot(int x) {int root = x;// 尋找根節點while (_ufs[root] >= 0) {root = _ufs[root];}// 路徑壓縮，將查找路徑上的每個節點直接連接到根節點while (_ufs[x] >= 0) {int parent = _ufs[x];_ufs[x] = root;x = parent;}return root;}// 檢查兩個元素是否屬于同一集合bool InSet(int x1, int x2) {return FindRoot(x1) == FindRoot(x2);}// 獲取并查集中集合的數量size_t SetSize() {size_t size = 0;for (size_t i = 0; i < _ufs.size(); ++i) {if (_ufs[i] < 0) {// 集合的根節點的值為負數，其絕對值表示集合的大小size++;}}return size;}private:std::vector<int> _ufs; // 并查集數組，非負值表示父節點的索引，負值的絕對值表示集合的大小
};

4.3 Prim算法

????????Prim算法（普里姆算法）的思路與Kruskal算法基本一致，采用的都是貪心策略，與Kruskal算法不同的是，Prim算法會選定一個起始點src，并將已經連通的頂點和尚未被連通的頂點劃分到兩個集合中去，分別記為S和U，每一次篩選，都會選出從si->ui的邊中權值最小的那個，由于對已經連通和尚未連通的頂點進行了劃分，因此選邊建立連接的過程中不需要并查集來輔助就能夠避免成環。下圖為Prim算法的選邊過程，紅色加粗的實線為被選擇的邊。

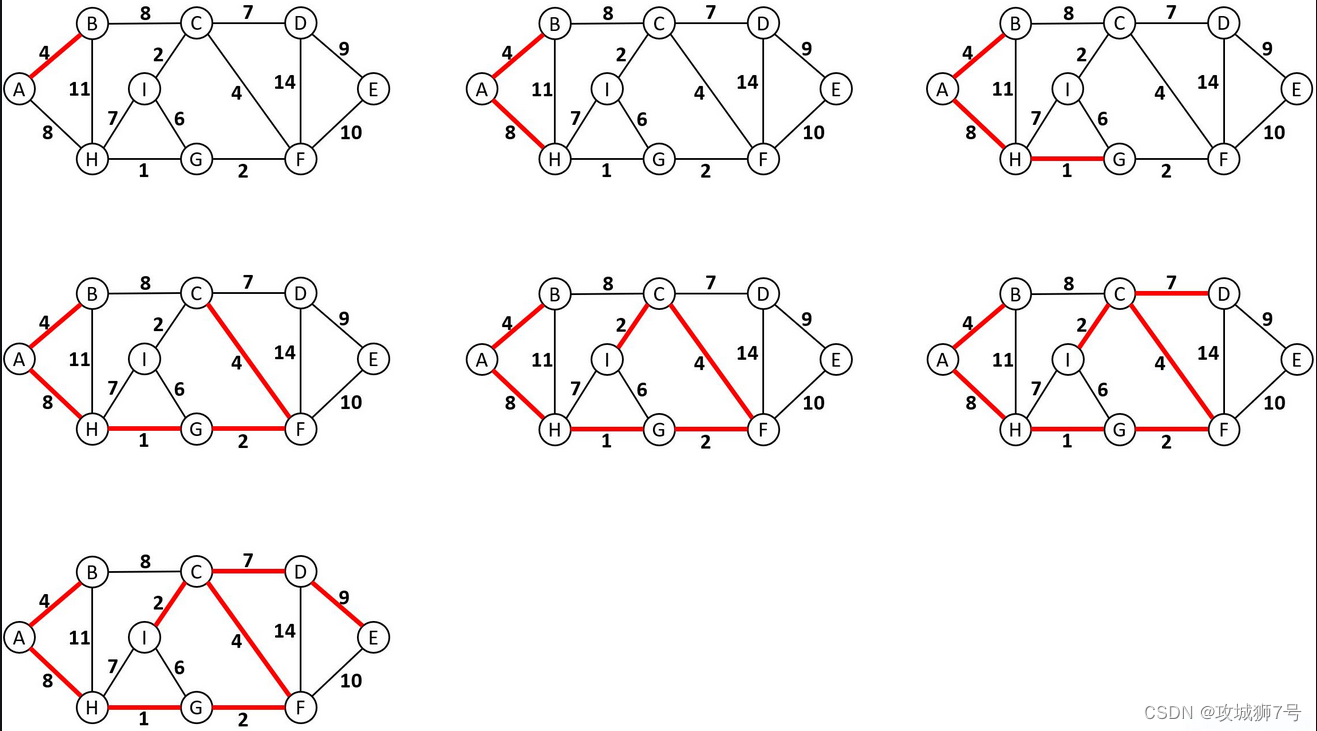
Prim算法的實現

// Prim算法獲取最小生成樹
template<class V, class W, W MAX_W = INT_MAX, bool Direction = false>
W Graph<V, W, MAX_W, Direction>::Prim(const V& src, Self& minTree) {// 初始化minTree的每個成員size_t n = _vertex.size();minTree._vertex = _vertex;minTree._valIndexMap = _valIndexMap;minTree._edges.resize(n, std::vector<W>(n, MAX_W));// 檢查源頂點是否存在auto it = _valIndexMap.find(src);if (it == _valIndexMap.end()) {throw std::runtime_error("源頂點不存在！");}size_t srci = it->second;// visited數組記錄每個頂點是否已經被訪問std::vector<bool> visited(n, false);visited[srci] = true; // 標記源頂點為已訪問// 使用小根堆選取最短邊std::priority_queue<Edge, std::vector<Edge>, std::greater<Edge>> minHeap;// 將源頂點的所有鄰邊加入小根堆for (size_t i = 0; i < n; ++i) {if (_edges[srci][i] != MAX_W) {minHeap.emplace(srci, i, _edges[srci][i]);}}size_t count = 0; // 已選擇的邊數W totalW = W();   // 最小生成樹的總權重std::cout << "Prim開始選邊：" << std::endl;// 循環直到所有頂點都被訪問或者堆為空while (!minHeap.empty() && count < n - 1) {// 獲取堆頂元素（最短邊）Edge curEdge = minHeap.top();minHeap.pop();size_t u = curEdge._srci;size_t v = curEdge._dsti;W w = curEdge._w;// 如果終點v未被訪問，則這條邊是最小生成樹的一部分if (!visited[v]) {std::cout << "[" << _vertex[u] << "->" << _vertex[v] << "]:" << w << std::endl;// 在minTree中添加這條邊minTree._AddEdge(u, v, w);// 更新訪問狀態，邊數和總權重visited[v] = true;++count;totalW += w;// 將新訪問到的頂點v的所有鄰邊加入小根堆for (size_t k = 0; k < n; ++k) {if (!visited[k] && _edges[v][k] != MAX_W) {minHeap.emplace(v, k, _edges[v][k]);}}}}// 如果選取的邊數等于頂點數減一，則成功構建了最小生成樹if (count == n - 1) {return totalW;} else {throw std::runtime_error("無法構建最小生成樹！");}
}

五、最短路徑問題

????????在所有類型的圖上，最短路徑問題都是尋找從一個頂點（或一組頂點）到另一個頂點（或一組頂點）的路徑，使得該路徑上所有邊的權重之和最小，權值非負情況。這通常通過使用適當的算法（如Dijkstra、Bellman-Ford、Floyd-Warshall等）來實現。

5.1 Dijkstra算法

????????Dijkstra算法（迪杰斯特拉算法），用于求單源最短路徑，即：給定一個起點，計算以這個頂點為起點，圖中其余任意頂點為終點的路徑中，權值之和最小的那一條路徑。注意，Dijkstra算法要求不能帶有負權值。

????????Dijkstra算法的核心思想是貪心算法，其大致的流程為：將一個有向圖G中的頂點分為S和Q兩組，其中S為已經確定了最短路徑的頂點，Q為尚未確定最短路徑的頂點，最初先將處源頂點srci以外所有頂點都加入Q，源頂點srci加入S。每次從Q中找出一個源頂點到該頂點最小的頂點u，將其從Q中移出放入到S中，對與u相鄰的頂點v進行松弛操作。所謂松弛操作，就是比較srci->u + s->v的和是否比原來srci->v的路徑和小，如果是，那么就更新srci->v的最短路徑，反復進行松弛操作，直到Q集合中沒有頂點。下圖為Dijkstra算法松弛迭代的過程，黑色填充的頂點為已經確定最短路徑的頂點，灰色填充為本輪遍歷的源頂點。

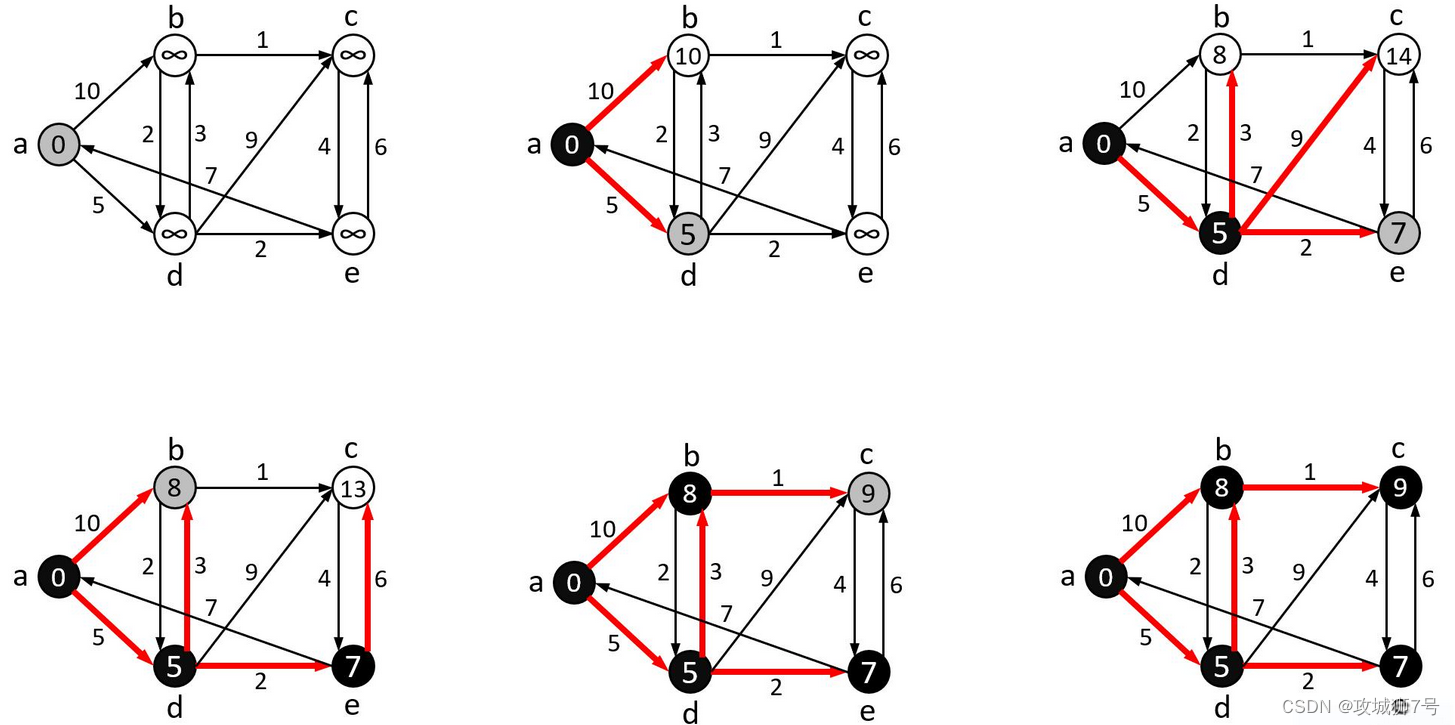
代碼實現

????????Dijkstra算法的具體實現，該函數接收三個參數，分別為起始點、最小路徑dist(輸出型參數)、每個頂點的父親頂點pPath(輸出型參數)，這里使用pPath的目的是為了避免存儲全部的路徑，達到節省空間，降低算法編碼難度的目的。為了觀察結果，實現了PrintPath函數，用于打印頂點src到任意頂點的最短路徑。

// Dijkstra算法求最短路徑
// dist為路徑和，pPath為每個頂點前導頂點的下標
template<class V, class W, W MAX_W = INT_MAX, bool Direction = false>
void Graph<V, W, MAX_W, Direction>::Dijkstra(const V& src, std::vector<W>& dist, std::vector<size_t>& pPath) {size_t n = _vertex.size();dist.assign(n, MAX_W);pPath.assign(n, std::numeric_limits<size_t>::max());// 獲取源頂點的下標auto srci = GetIndex(src);if (srci >= n) {throw std::runtime_error("源頂點不存在！");}dist[srci] = 0;pPath[srci] = srci;std::vector<bool> visited(n, false);for (size_t k = 0; k < n; ++k) {// 找出未訪問頂點中dist最小的W minDist = MAX_W;size_t u = std::numeric_limits<size_t>::max();for (size_t i = 0; i < n; ++i) {if (!visited[i] && dist[i] < minDist) {minDist = dist[i];u = i;}}// 所有頂點都訪問過或者剩下的頂點都不可達if (u == std::numeric_limits<size_t>::max()) break;visited[u] = true;for (size_t v = 0; v < n; ++v) {if (!visited[v] && _edges[u][v] != MAX_W && dist[u] + _edges[u][v] < dist[v]) {dist[v] = dist[u] + _edges[u][v];pPath[v] = u;}}}
}// 路徑打印函數
template<class V, class W, W MAX_W = INT_MAX, bool Direction = false>
void Graph<V, W, MAX_W, Direction>::PrintPath(const V& src, const std::vector<W>& dist, const std::vector<size_t>& pPath) {size_t srci = GetIndex(src);size_t n = _vertex.size();for (size_t i = 0; i < n; ++i) {if (dist[i] == MAX_W) {std::cout << _vertex[srci] << "->" << _vertex[i] << " 不可達" << std::endl;continue;}std::vector<size_t> path;for (size_t v = i; v != srci; v = pPath[v]) {if (pPath[v] == std::numeric_limits<size_t>::max()) {std::cout << _vertex[srci] << "->" << _vertex[i] << " 不可達" << std::endl;break;}path.push_back(v);}path.push_back(srci);std::reverse(path.begin(), path.end());for (size_t j = 0; j < path.size(); ++j) {std::cout << _vertex[path[j]];if (j < path.size() - 1) std::cout << "->";}std::cout << " 權重:" << dist[i] << std::endl;}
}

5.2 Bellman-Ford算法

????????Dijkstra算法不能解決帶有負權的圖的問題，為此，Bellman-Ford算法（貝爾曼-福特算法）被提了出來，這種算法可以解決帶有負權的圖的最小路徑問題，這種算法也是用于解決單源最短路徑問題的，即：給定一個起始點src，獲取從src到每一個頂點的最短路徑。

????????Bellman-Ford算法實際上是一種暴力求解的算法，對于有N個頂點的圖，要暴力搜索頂點vi和頂點vj，迭代更新最短路徑。Bellman-Ford算法的時間復雜度為O(N^3)，而Dijkstra算法的時間復雜度為O(N^2)，因此對于不帶有負權的圖，應當使用Dijkstra求最短路徑而非使用Bellman-Ford算法

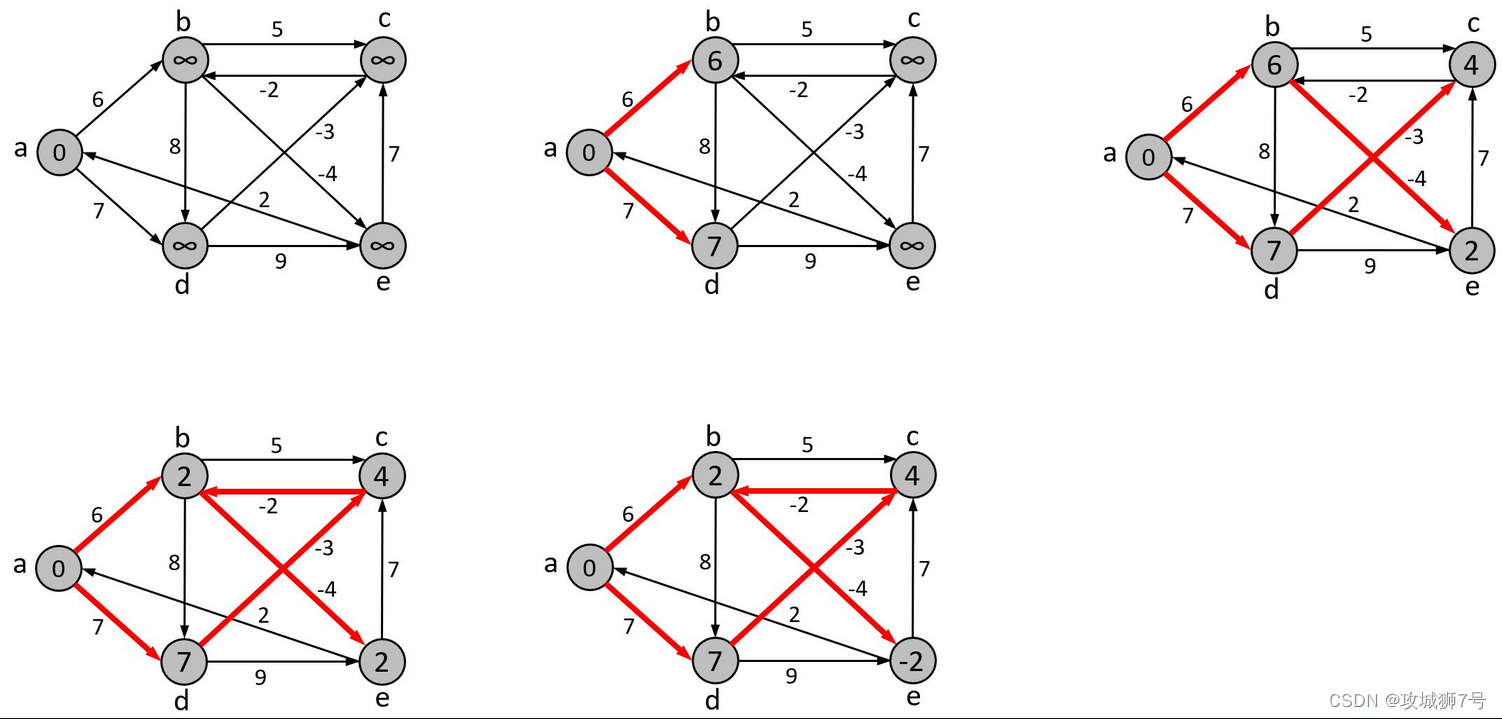
????????Bellman-Ford算法無法解決負權回路，所謂負權回路，就是圖結構中的某個環，其所有邊的權值累加起來小于0，就是負權回路。如下所示的圖，a->b->d->a就是一個負權回路，a->b->d->a的權值加起來為-2，這樣就存在一種詭異的現象，即每一次從a出發再回到a，路徑權值之和都會變小，這樣理論上a->a的路徑可以無限小，對于存在負權回路的圖，沒有任何辦法可以解決其最小路徑問題。

代碼實現：Bellman-Ford算法的實現

// BellmanFord算法求單源最短路徑
// dist為路徑長度數組，pPath為各頂點的前導頂點下標
template<class V, class W, W MAX_W = std::numeric_limits<W>::max()>
bool Graph<V, W, MAX_W>::BellmanFord(const V& src, std::vector<W>& dist, std::vector<size_t>& pPath) {size_t n = _vertex.size();dist.assign(n, MAX_W);pPath.assign(n, std::numeric_limits<size_t>::max());size_t srci = GetIndex(src);    // 獲取源頂點的下標if (srci >= n) {throw std::runtime_error("源頂點不存在！");}dist[srci] = 0;                 // 源點到自身的距離為0pPath[srci] = srci;             // 源點的前導節點設為自身// 進行n-1輪松弛操作，確保所有的最短路徑都被找到for (size_t k = 0; k < n - 1; ++k) {bool updated = false;       // 用于標記本輪是否有更新// 遍歷所有邊進行松弛操作for (size_t i = 0; i < n; ++i) {for (size_t j = 0; j < n; ++j) {if (dist[i] != MAX_W && _edges[i][j] != MAX_W &&dist[i] + _edges[i][j] < dist[j]) {dist[j] = dist[i] + _edges[i][j];pPath[j] = i;updated = true;}}}// 如果本輪沒有更新，則提前退出if (!updated) {break;}}// 檢查負權回路，如果存在則返回falsefor (size_t i = 0; i < n; ++i) {for (size_t j = 0; j < n; ++j) {if (_edges[i][j] != MAX_W && dist[i] + _edges[i][j] < dist[j]) {return false;  // 存在負權回路}}}return true;  // 不存在負權回路
}

5.3 Floyd-Warshall算法

????????Floyd-Warshall算法（弗洛伊德算法），是用于計算多源最短路徑的算法，其基本原理為三維動態規劃算法：

設D_{ijk}為，從頂點i到定點j，僅以 {1,2,...,k}頂點為中間頂點的情況下的最短路徑和。

??? 若i->j的最短路徑經過k，那么D_{i,j,k} = D_{i,j,k-1}+D_{k,j,k-1}
??? 如i->j的最短路徑不經過k，那么D_{i,j,k}=D_{i,j,k-1}

狀態轉移方程為：D_{i,j,k}=min(D_{i,j,k-1}+D_{k,j,k-1}, D_{i,j,k-1})

????????Floyd-Warshall算法的本質是三維動態規劃算法，D[i][j][k]表示的是從頂點i到頂點j，在只經過0~k個中間頂點的情況下的最短路徑。通過優化將最后一維k優化掉，這是只需要二維數組D[i][j]就可以計算出多源最短路徑，Floyd-Warshall算法的時間復雜度為O(N^3)，空間復雜度為O(N^2)，且Floyd-Warshall算法可以解決帶有負權的圖的問題。

代碼實現：Floyd-Warshall算法的實現

// FloydWarshall算法計算所有頂點對之間的最短路徑
template<class V, class W, W MAX_W = std::numeric_limits<W>::max()>
void Graph<V, W, MAX_W>::FloydWarshall(std::vector<std::vector<W>>& vvDist, std::vector<std::vector<size_t>>& vvPath) {size_t n = _vertex.size();vvDist.assign(n, std::vector<W>(n, MAX_W));vvPath.assign(n, std::vector<size_t>(n, std::numeric_limits<size_t>::max()));// 初始化距離和路徑矩陣for (size_t i = 0; i < n; ++i) {for (size_t j = 0; j < n; ++j) {if (_edges[i][j] != MAX_W) {vvDist[i][j] = _edges[i][j];vvPath[i][j] = i;}if (i == j) {vvDist[i][j] = 0;  // 頂點到自身的距離為0vvPath[i][j] = i;  // 頂點到自身的路徑是自己}}}// 使用動態規劃方法更新所有頂點對之間的最短路徑for (size_t k = 0; k < n; ++k) {for (size_t i = 0; i < n; ++i) {for (size_t j = 0; j < n; ++j) {if (vvDist[i][k] != MAX_W && vvDist[k][j] != MAX_W &&vvDist[i][k] + vvDist[k][j] < vvDist[i][j]) {vvDist[i][j] = vvDist[i][k] + vvDist[k][j];vvPath[i][j] = vvPath[k][j];  // 更新路徑}}}}
}

六、AOV網絡和AOE網絡

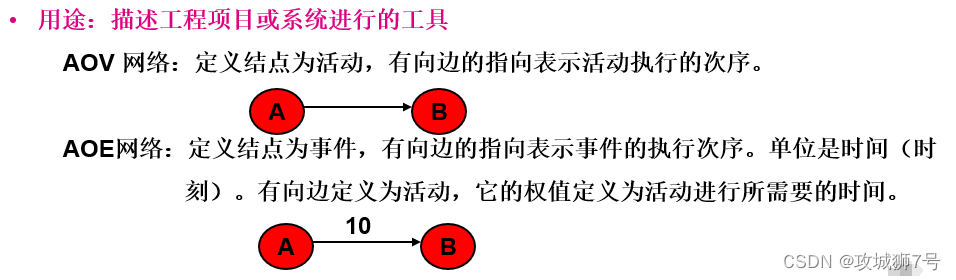
????????AOV網絡和AOE網絡是數據結構中用于表示和分析工程計劃和實施過程的有向無環圖（DAG）的兩種不同方式。DAG圖差異如下所示

以下是關于這兩種網絡的詳細解釋：

6.1 AOV網絡（Activity On Vertex Network）

定義：AOV網絡是用頂點表示活動，用有向邊表示活動之間的先后關系的有向圖123。在實際應用中，例如工程或項目的計劃中，各個子工程或任務被表示為圖中的頂點，而它們之間的依賴關系或執行順序則用有向邊來表示。

特點：

頂點表示活動（或任務）。
有向邊表示活動之間的先后關系。
可以通過拓撲排序獲得活動的執行順序。
在AOV網中，并發活動可以被表示為互不相連的頂點。

應用：AOV網絡常被用于現代化管理，來描述和分析一項工程的計劃和實施過程，形象地反映出整個工程中各個活動之間的先后關系。

6.2 AOE網絡（Activity On Edge Network）

定義：AOE網絡是在帶權有向圖中，用頂點表示事件（即活動的起始和結束時間），用有向邊表示活動，邊上的權值表示活動的持續時間。這樣的圖用來估算工程的最短工期以及哪些活動是影響工程進展的關鍵。

特點：

頂點表示事件（活動的起始和結束時間）。
有向邊表示活動，邊上的權值表示活動的持續時間。
需要進行關鍵路徑的計算，以確定整個項目的最短完成時間和關鍵活動。
在AOE網中，并發活動可以通過將多個活動指向同一個事件節點來表示。

應用：AOE網絡用于描述由許多交叉活動組成的復雜計劃和工程的方法，如計算工程的最短工期和識別關鍵路徑等。

6.3 異同點

定義：AOV網將活動表示為圖中的頂點，活動之間的依賴關系表示為有向邊；而AOE網將活動表示為圖中的邊，邊上的權值表示活動的持續時間，頂點表示事件。
表示方式：在C語言中，AOV網常用鄰接表或鄰接矩陣來表示；而AOE網則需要引入事件節點，用鄰接表表示圖。
拓撲排序：AOV網可以通過拓撲排序獲得活動的執行順序；而AOE網則需要進行關鍵路徑的計算。

總之，AOV網絡和AOE網絡在數據結構中的表示和計算方式上有一些不同。AOV網更關注活動的依賴關系和執行順序，而AOE網更關注活動的持續時間和項目的最短完成時間。有興趣的可以自行了解各方面的應用。

七、總結

????????圖是一種用于存儲頂點和邊之間關系的數據結構，記作G={V,E}，其中V代表頂點的集合，E代表邊的集合。根據邊是否帶有權重以及邊的方向性，圖可以進一步細分為帶權圖與無權圖、有向圖與無向圖。

????????圖的存儲結構主要有兩種：鄰接表和鄰接矩陣。這兩種方式各有其適用場景和優缺點。在表示稀疏圖時，鄰接表因其節省空間的特性而常用；然而，在表示稠密圖時，由于鄰接矩陣的索引方式簡單直觀，且便于計算圖中任意兩點之間的路徑，因此通常選擇鄰接矩陣作為存儲結構。

????????在無向連通圖中，最小生成樹是一個特殊的子圖，它包含了原圖中的所有頂點，并且這些頂點之間通過邊相連，形成一個沒有回路的樹形結構。同時，這棵樹的邊權值之和是所有可能的樹中最小的。計算最小生成樹常用的算法有Kruskal算法和Prim算法，這兩種算法都采用了局部貪心的策略。

????????Dijkstra算法和Bellman-Ford算法是解決單源最短路徑問題的經典算法。Dijkstra算法適用于邊權值為非負的圖，能夠高效地計算出從指定源點到圖中其他所有頂點的最短路徑。然而，當圖中存在負權邊時，Dijkstra算法將不再適用。Bellman-Ford算法則能夠處理帶有負權邊的圖，但相對于Dijkstra算法，其時間復雜度較高。Dijkstra算法的時間復雜度為O(N^2)（其中N為頂點的數量），而Bellman-Ford算法的時間復雜度為O(N^3)。

????????Floyd-Warshall算法則用于解決多源最短路徑問題，即計算圖中任意兩點之間的最短路徑。該算法基于動態規劃的思想，能夠處理帶有負權邊的圖。其時間復雜度為O(N^3)，其中N為頂點的數量。

????????AOV網絡和AOE網絡都是用于描述和分析工程項目中活動之間關系的有向無環圖數據結構。
????????AOV網絡側重于活動之間的依賴關系和執行順序，通過拓撲排序確定活動的合理執行順序。
????????AOE網絡側重于活動的持續時間和項目的最短完成時間，通過計算關鍵路徑來估算工程完成時間和確定關鍵活動。在實際應用中，根據項目需求的不同，可以選擇使用AOV網絡或AOE網絡來進行項目規劃和分析。