矩陣和標量的運算
,則
矩陣與矩陣相乘
的矩陣A,
的矩陣B。兩矩陣
,結果為
的矩陣,第一個矩陣的列數必須和第二個矩陣的行數相同,否則不能相乘
,
中的每個元素等于A的第i行所對應的矢量和B的第j列所對應的矢量進行矢量點乘的結果
即
注意:矩陣乘法不滿足交換律
矩陣乘法滿足結合律
Shader中常用矩陣
1.方塊矩陣(方陣)(square matrix):行數和列數相等的矩陣。
2.對角矩陣:如果一個方陣除了對角元素外的所有元素都為0,那么這個方陣為對角矩陣。
3.單位矩陣:特殊的對角矩陣,用表示,例如
的單位矩陣為
。?
4.轉置矩陣:原矩陣為
,它的轉置表示為
,轉置矩陣的運算為原矩陣的第
行變成第
列,第
列變成第
行。
,示例
轉置矩陣常用性質
性質一:矩陣轉置的轉置等于原矩陣????????
性質二:矩陣串接的轉置等于反向串接各個矩陣的轉置? ? ? ??
5.逆矩陣
給定一個矩陣,它的逆矩陣為
,把
和
相乘,結果為一個單位矩陣,即
矩陣有逆矩陣的前提為該矩陣為方陣且并非所有元素都為0。
逆矩陣的常用性質
性質一:逆矩陣的逆矩陣是原矩陣本身,即
性質二:單位矩陣的逆矩陣是它本身,即
性質三:轉置矩陣的逆矩陣是逆矩陣的轉置,即
性質四:矩陣串接相乘后的逆矩陣等于反向串接各個矩陣的逆矩陣,即
三維變換與投影
現實世界是三維的,要在二維屏幕上繪制出三維場景需要通過投影變換降低維數。
三維變換矩陣
三維變換引入齊次坐標,在四維空間內進行研究。
三維變換可表示為某一變換矩陣與物體頂點集合的齊次坐標矩陣相乘的形式,三維變換矩陣是的方陣。
例如:
為
的子矩陣,用于對物體進行比例、旋轉、反射、錯切變換。
為
的子矩陣,用于對物體進行平移變換。
為
子矩陣,用于對物體進行投影變換。
為
子矩陣,用于對物體進行整體比例變換。
三維變換形式
三維變換的基本方法是把矩陣作為算子,作用到變換前的物體頂點集合的齊次坐標矩陣上,得到變換后新的頂點集合的齊次坐標矩陣,連接新的物體頂點,可繪制出變換后的三維物體模型。
設變換前的物體頂點矩陣
變換后的物體頂點矩陣
則三維變換公式為,即
三維基本變換
三維基本變換是指將點從一個坐標位置變換到另一個坐標位置
的過程,是相對于坐標系或坐標軸進行的幾何變換。
平移變換
、
、
為平移參數
平移變換的坐標表示為
三維平移變換矩陣為
比例變換
、
、
為比例系數
比例變換的坐標表示為
三維比例變換矩陣為
旋轉變換
三維旋轉變換一般看作二維旋轉變換的組合,可分為繞軸旋轉、繞
軸旋轉、繞
軸旋轉,繞坐標軸旋轉角用
表示,
正向定義符合右手螺旋定則,大拇指指向旋轉軸正向,其余四指的轉向為轉角的正向。
繞 軸旋轉
軸旋轉
為正向旋轉角
繞軸旋轉變換的坐標表示為
繞軸旋轉三維變換矩陣為
繞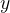 軸旋轉
軸旋轉
為正向旋轉角
繞軸旋轉變換的坐標表示為
繞軸旋轉三維變換矩陣為
繞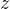 軸旋轉
軸旋轉
為正向旋轉角
繞軸旋轉變換的坐標表示為
繞軸旋轉三維變換矩陣為
反射變換
三維反射分為關于坐標軸的反射和關于坐標平面的反射兩類。
關于 軸的反射
軸的反射
關于軸反射變換的坐標表示為
關于軸的三維反射變換矩陣為
關于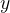 軸的反射
軸的反射
關于軸反射變換的坐標表示為
關于軸的三維反射變換矩陣為
關于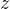 軸的反射
軸的反射
關于軸反射變換的坐標表示為
關于軸的三維反射變換矩陣為
關于 平面的反射
平面的反射
關于平面反射變換的坐標表示為
關于平面的三維反射變換矩陣為
關于 平面的反射
平面的反射
關于平面反射變換的坐標表示為
關于平面的三維反射變換矩陣為
關于 平面的反射
平面的反射
關于平面反射變換的坐標表示為
關于平面的三維反射變換矩陣為

】Linux的進程和計劃任務管理)




)

)
)



 變量與環境:文法結構 | 真假表達式:isZero E | let 表達式疊放 | 定義的規則 | 條件語句的使用)


macros模塊)

)
