任務空間運動控制簡介

任務空間運動控制—位置被指定給控制器作為末端執行器的姿態。然后，控制器驅動機器人的關節配置到使末端執行器移動到指定姿態的值。這有時被稱為操作空間控制。
任務空間運動模型表示機器人在閉環任務空間位置控制下的運動，可使用Task Space Motion Model模塊進行控制。
機器人機械手是典型的位置控制設備。要進行任務空間控制，需要在SE(3)中指定一個參考末端執行器姿態，然后模型會返回關節配置向量 q 及其狀態導數，可對機器人關節進行閉環控制，并使用運動模型模擬機器人在此控制下的動作。

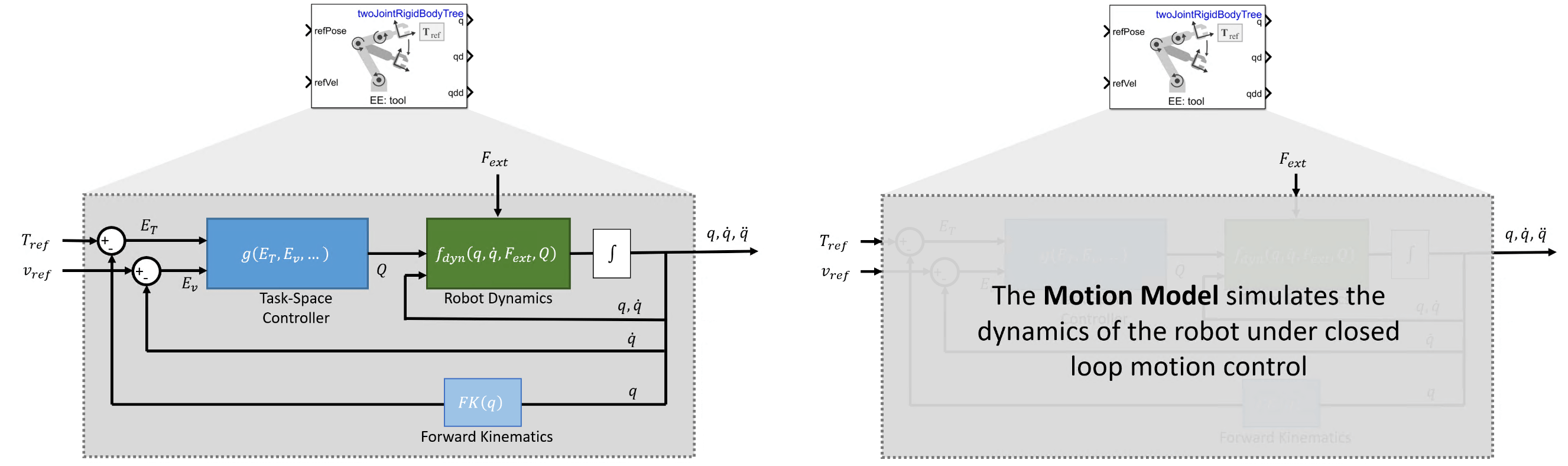
要使這種方法最接近實際系統的運動，必須準確表示控制器和被控對象的動態顯示狀態。雖然任務空間控制有很多不確定性，但Task Space Motion Model模塊使用的是相對簡單的Jacobian-Transpose方法（雅可比矩陣轉置法），當機器人和控制器的動態參數經過精調之后，該方法的控制較為精確。

關鍵變量

該模型的狀態變量有：

• $q$—機器人關節配置，作為關節位置的矢量。對于旋轉副單位為：$rad$，對于平移副單位為：$m$。
• $\dot{q}$—機器人關節速度矢量，對于旋轉副單位為：$rad/s$，對于平移副單位為：$m/s$。
• $\ddot{q}$—機器人關節加速度矢量，對于旋轉副單位為：$rad/s^2$，對于平移副單位為：$m/s^2$。

機器人的末端執行器姿態$T(q)$是一個 4 * 4 的齊次變換矩陣，相對于機器人基座的原點定義。位置單位為米。T 的兩種形式用于計算控制誤差：

• $T_{ref}$ - 參考末端執行器位姿，指定為期望的末端執行器位姿。
• $T_{act}$ - 實際末端執行器實際位姿末端執行器變換分解為:

$$T = \left[ {\matrix{
R & X \cr
0 & 1 \cr

} } \right]$$

R為3 * 3的旋轉矩陣，X為3 * 1的位置矩陣。

PD控制器

當運動模型使用PD控制（可使用taskSpaceMotionModel模塊）時，模型使用標準剛體動力學計算正向動力學，但受制于 PD 控制律，該控制器作用于期望姿態與實際末端執行器姿態之間的誤差。

• 輸入 - 該模型接受參考姿態$T_{ref}$和參考末端執行器速度$v_{ref}$。
• 輸出 - 模型反饋的$q、\dot{q}、\ddot{q}$即為關節的角度、速度和加速度。
• 復雜性 - 模型的復雜性描述了所需的總體計算量。這是一個中等復雜度的運動模型。它使用完整的剛體動力學，但模型中使用的控制法則相對簡單。

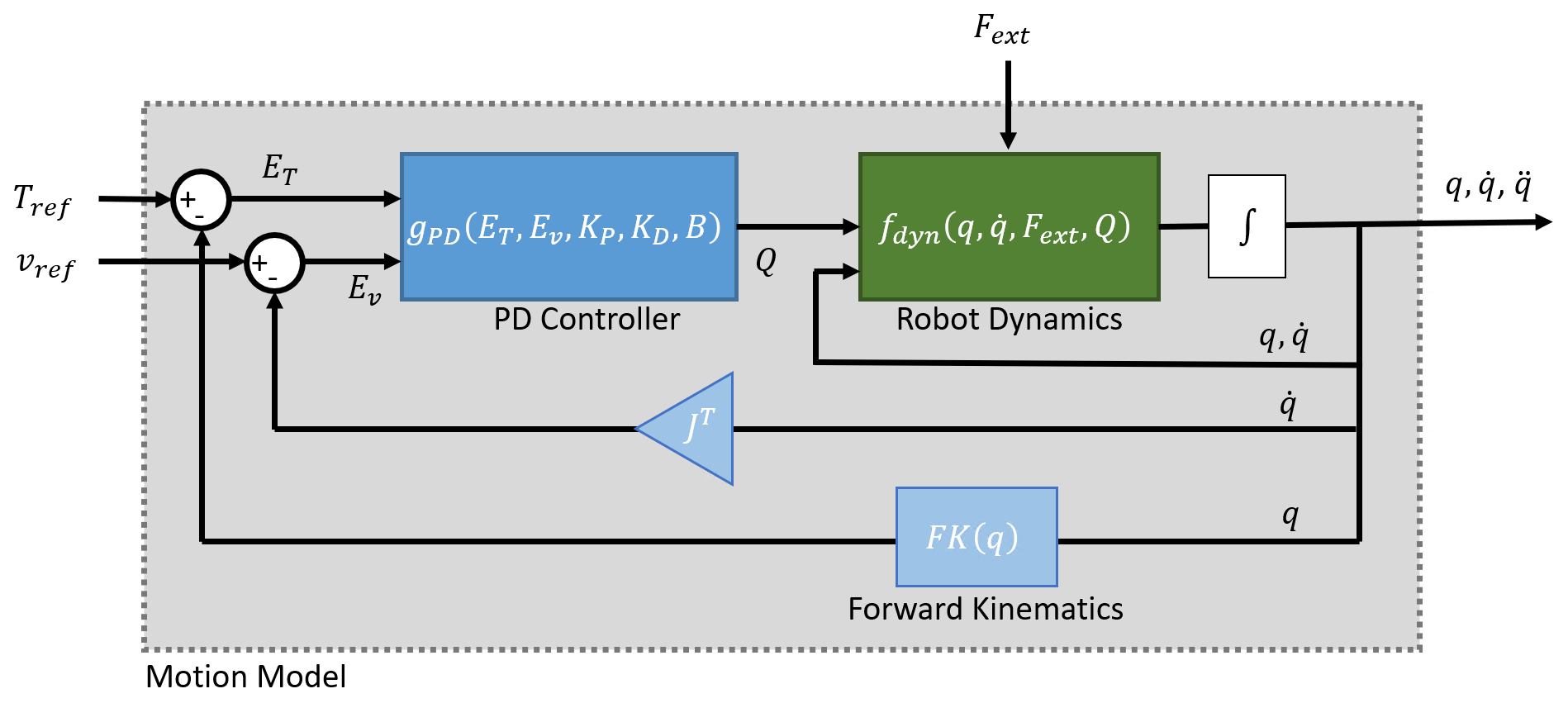
在該系統中，關節位置、速度和加速度均采用標準剛體機器人動力學計算。廣義力輸入 Q 由任務空間誤差的 PD 控制器法提供，并通過雅可比轉置法縮放至關節空間：

• $e_{rot}$ - 是使用 rotm2eul(RrefRTact) 轉換為歐拉角的旋轉誤差。
• $e_{pos}$ - 是 xyz 坐標誤差，計算公式為 $X_{ref}?X_{act}$。
• G(q) - 是所有關節在指定重力下保持其位置的重力扭矩和力。
• J(q) - 是給定關節配置的幾何雅各布系數，更多信息，請參閱幾何雅各布系數函數。

控制輸入依賴于這些用戶定義的參數：

• KP - 比例增益，以 6×6 矩陣形式指定

• KD - 微分增益，指定為 6 x 6 矩陣

• B - 關節阻尼矢量，指定為雙元素阻尼常數矢量，對旋卷關節而言單位為 N?s?rad-1，對棱柱關節而言單位為 N?s?m-1

該模型輸入：

$T_{ref}$ - 參考末端執行器姿勢，指定為所需的末端執行器姿勢

$v_{ref}$ - 參考末端執行器速度，指定為矢量

包含角速度$\omega $和平移速度${\dot X}$.

往期推薦