P1972 [SDOI2009] HH的項鏈

[SDOI2009] HH的項鏈

題目描述

HH 有一串由各種漂亮的貝殼組成的項鏈。HH 相信不同的貝殼會帶來好運，所以每次散步完后，他都會隨意取出一段貝殼，思考它們所表達的含義。HH
不斷地收集新的貝殼，因此，他的項鏈變得越來越長。

有一天，他突然提出了一個問題：某一段貝殼中，包含了多少種不同的貝殼？這個問題很難回答……
因為項鏈實在是太長了。于是，他只好求助睿智的你，來解決這個問題。

輸入格式

一行一個正整數 $n$，表示項鏈長度。 第二行 $n$ 個正整數 $a_i$，表示項鏈中第 $i$ 個貝殼的種類。

第三行一個整數 $m$，表示 HH 詢問的個數。 接下來 $m$ 行，每行兩個整數 $l,r$，表示詢問的區間。

輸出格式

輸出 $m$ 行，每行一個整數，依次表示詢問對應的答案。

樣例 #1

樣例輸入 #1

6 1 2 3 4 3 5 3 1 2 3 5 2 6

樣例輸出 #1

2 2 4

提示

【數據范圍】

對于 $20\%$ 的數據，$1\le n,m\le 5000$； 對于 $40\%$ 的數據，$1\le n,m\le 10^5$； 對于 $60\%$ 的數據，$1\le n,m\le 5\times 10^5$； 對于 $100\%$
的數據，$1\le n,m,a_i\le 10^6$，$1\le l\le r\le n$。

本題可能需要較快的讀入方式，最大數據點讀入數據約 20MB

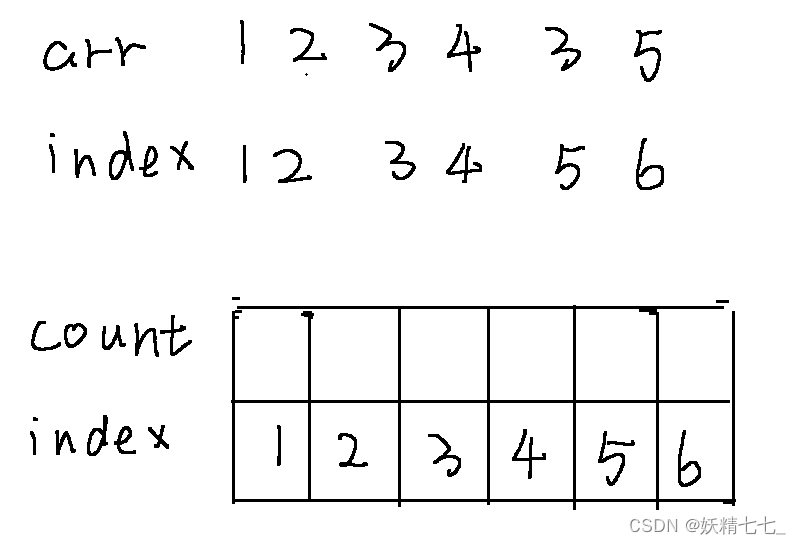
用count數組記錄每一個位置種類數,實際上每一個位置都算作是1.
如果每一個位置都是1.

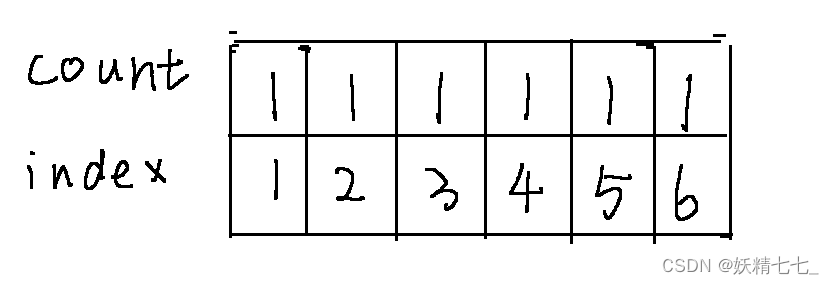
計算1~ 4區間的種類數是1~ 4區間count數組的累加和結果.
因為1~ 4區間中的種類數全部都沒有出現重復的情況.
但是如果要計算3~ 5區間的種類數是多少,那么就需要對3和5哪一個位置進行去重的處理.

如果我們查詢的區間是l~ r.

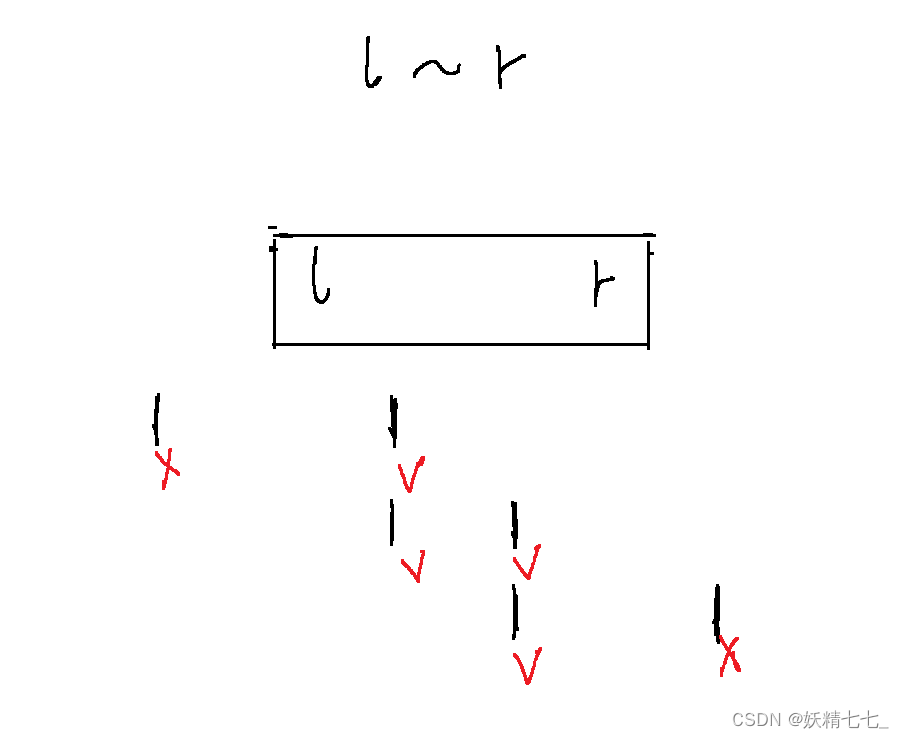
1表示重復的種類的1出現的位置,那么打叉的地方是需要進行去重的,打勾的地方是可以選擇保留的地方.
針對于第三種情況,r右邊出現的1我們并不關心,因為一定不在查詢區間中.
因此可以按照查詢的右區間從小到大排序,只維護r左邊count值即可.
現在我們就只需要維護好r左邊的count值就可以了.
也就是第一種情況和第二種情況,第二種情況因為都在區間內,所以不管去掉哪一個都可以,但是第一種情況只能去掉左邊的.
因此我們可以按照這樣的規則,只保留最右邊的1.因為如果包含最右邊的1,其他的可以被代替,如果沒有包含最右邊的1,其他的1也沒有意義.
所以只需要關心最右邊的1即可.

按照查詢的右區間進行排序,然后只維護r左邊的count值.
當前位置是i=1位置,然后維護1~ r區間的count值,每一次都添加1,但是每一次遍歷i位置的時候需要考慮是否需要去重操作.
也就是需要查詢arr[i]元素最右側的1是否出現,如果出現了就需要先減少1.

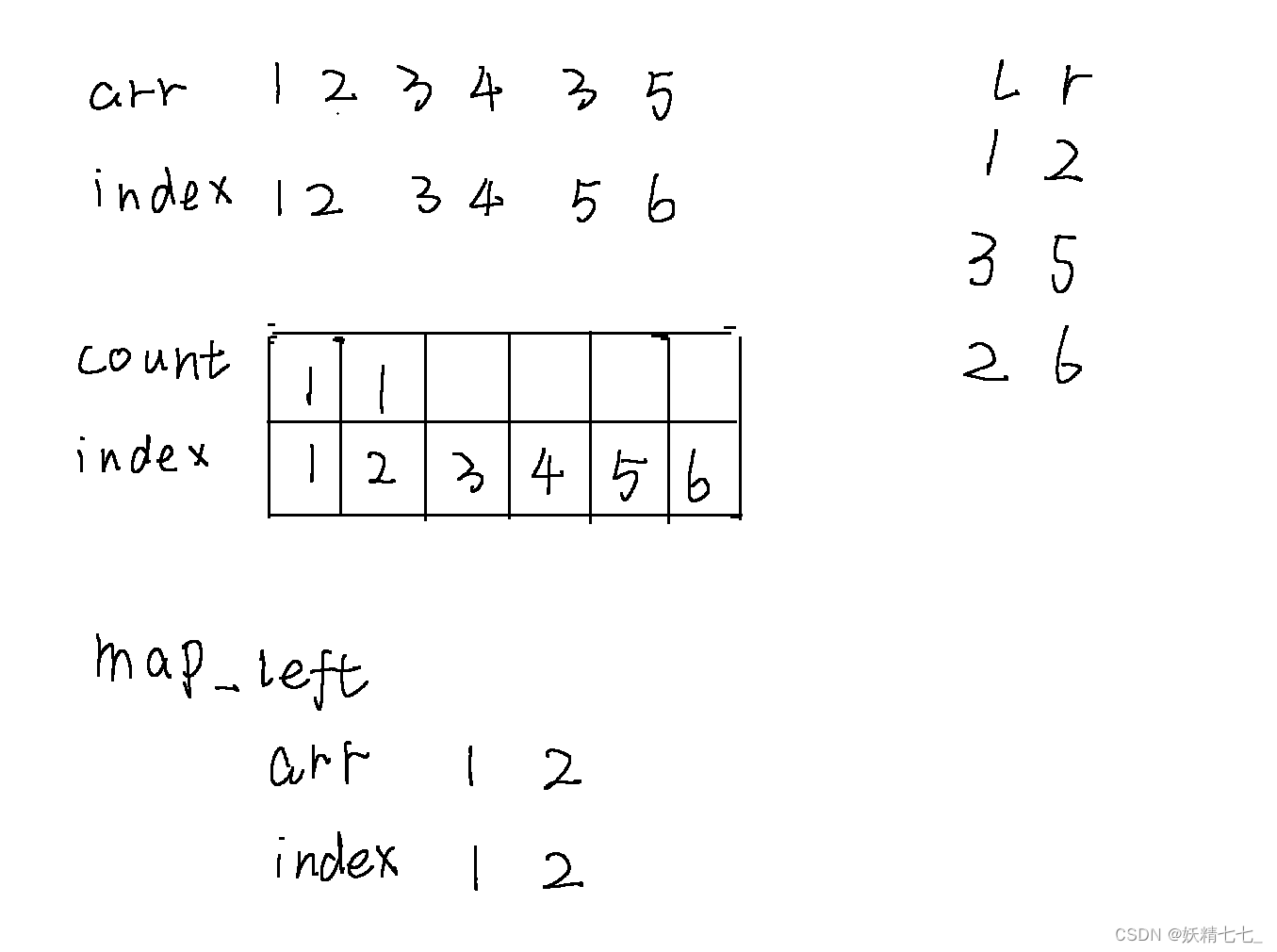
第一次查詢結果是count數組1~ 2累加和,答案是2

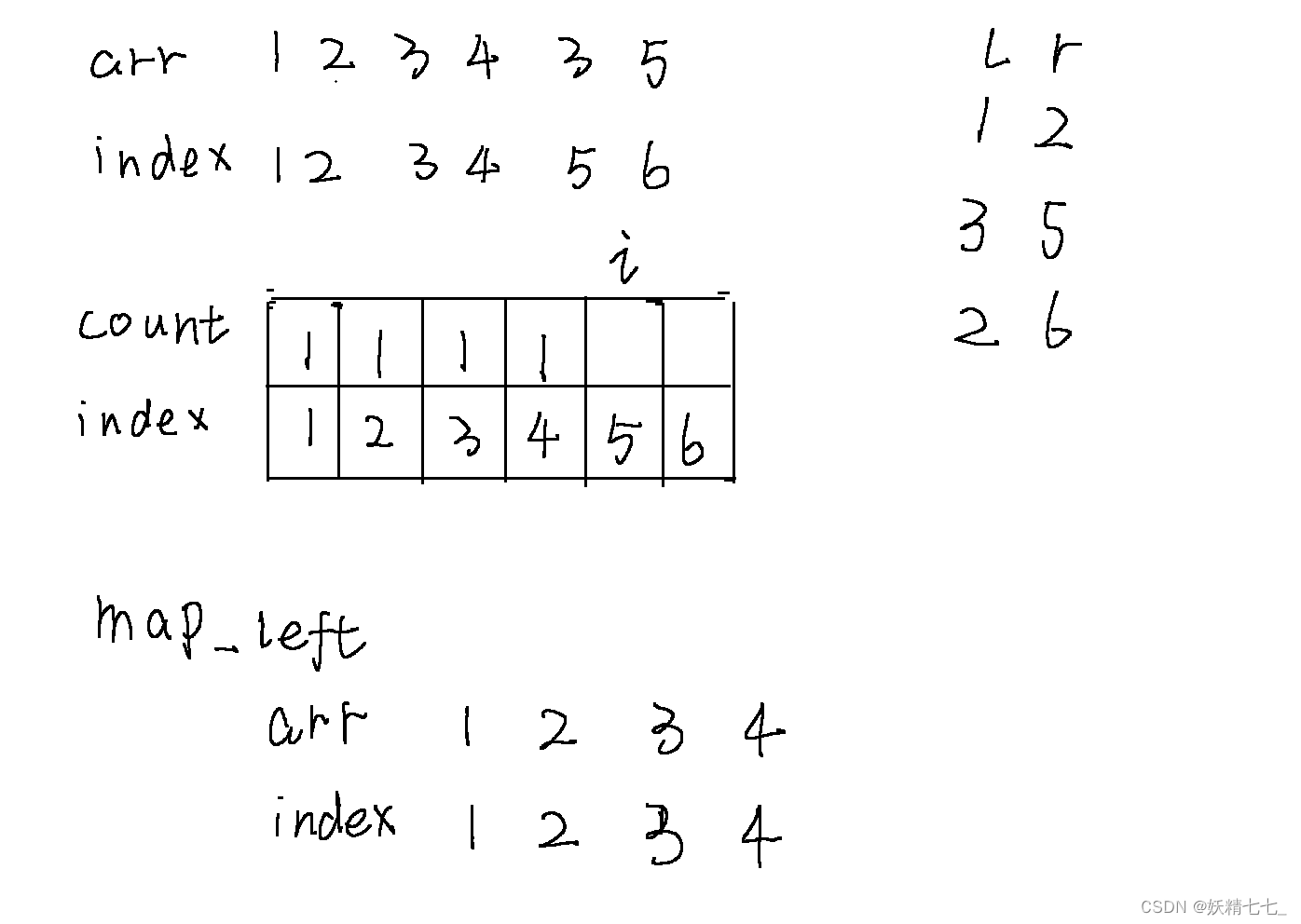
當i遍歷到5的時候,我們查詢map_left發現5位置的元素3之前出現過,位置是3,所以需要進行去重操作,將3位置count值減少1,然后5位置count值增加1.并且將維護arr_left值,元素3最右邊的下標是5.

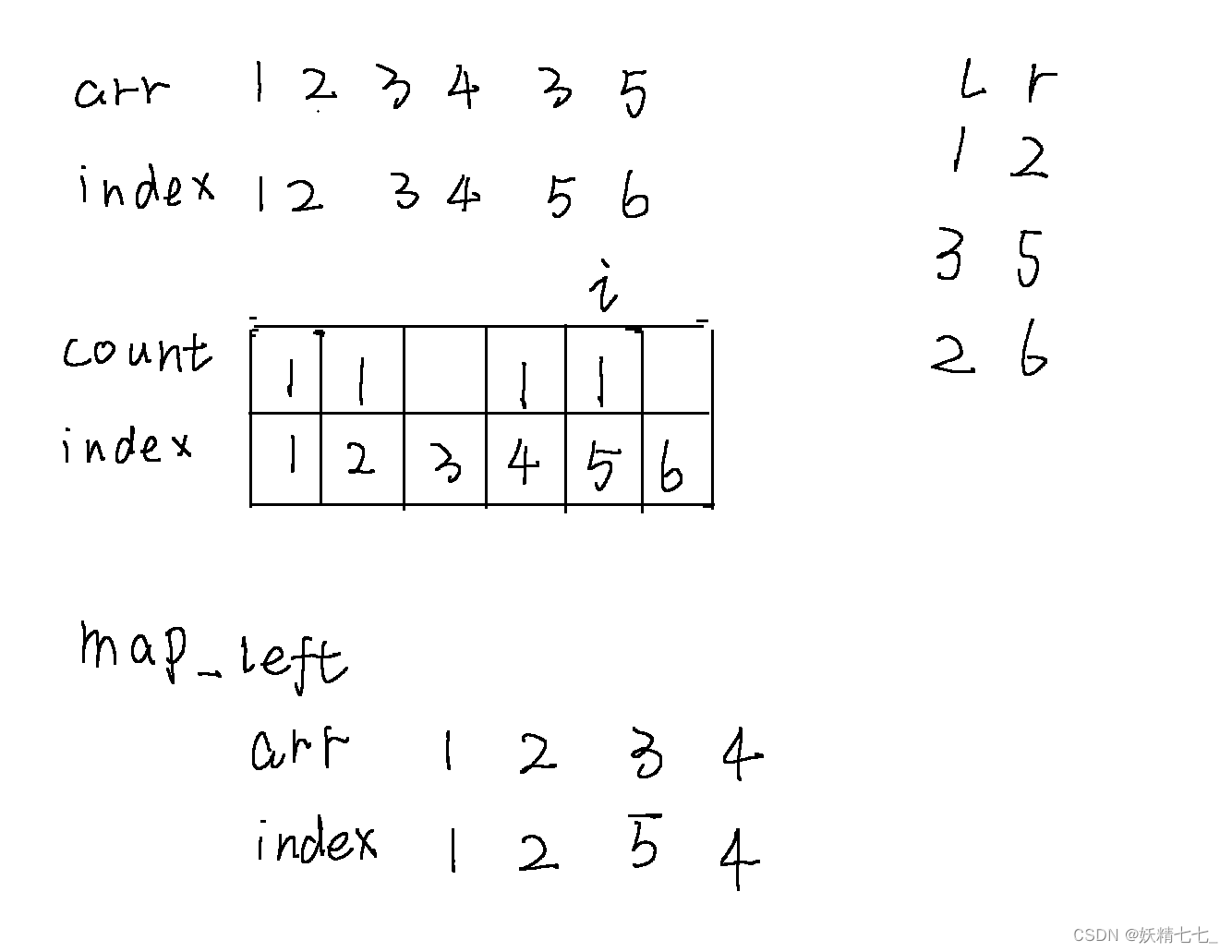
此時查詢3~ 5區間的種類數是count3~ 5區間累加和,答案是2.

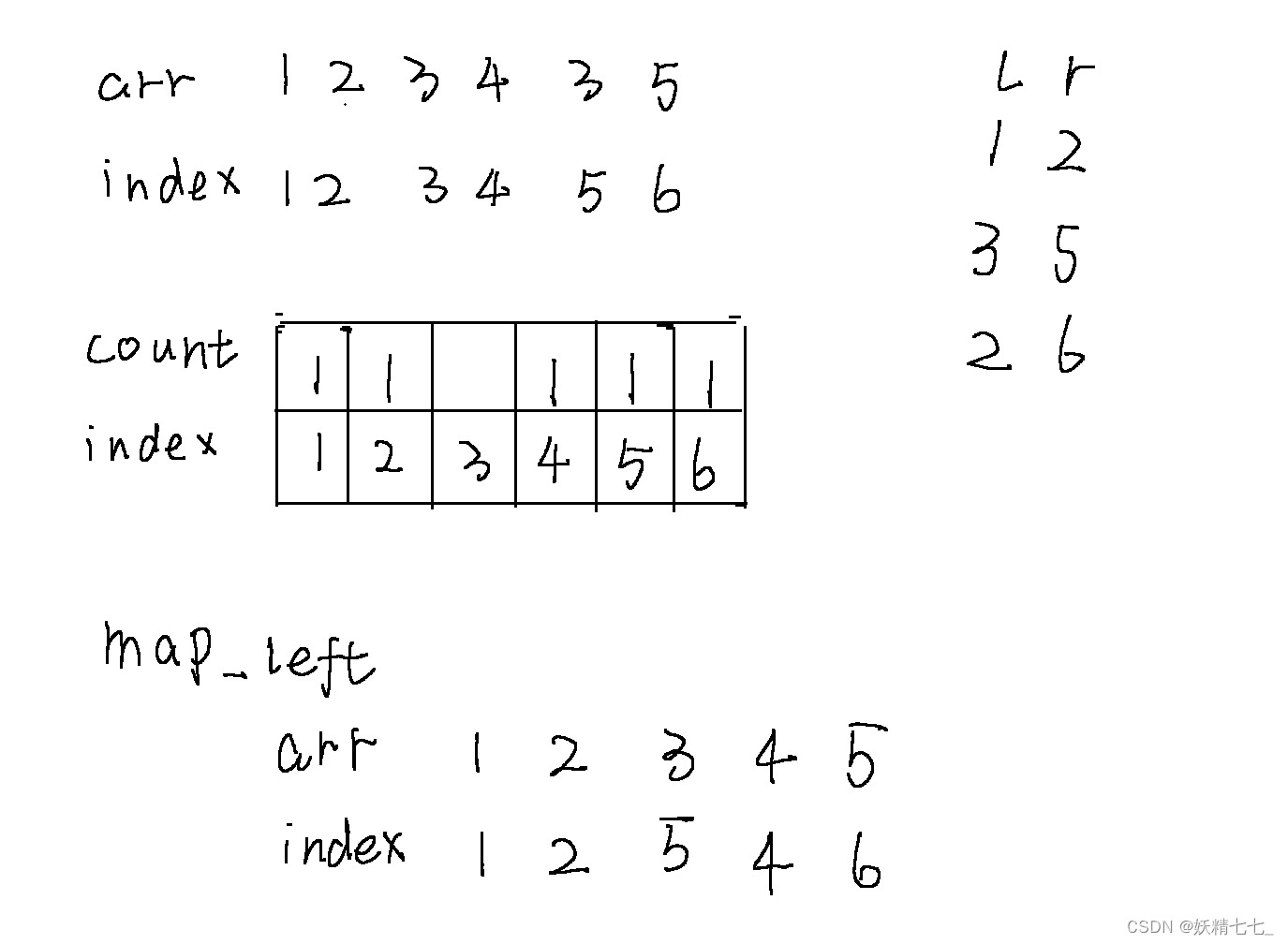
查詢2~ 6區間的種類數,也就是count2~ 6區間累加和,答案是4.

#include<bits/stdc++.h>
using namespace std;#define int long long // 將 int 定義為 long long 類型
#define endl '\n' // 將 endl 定義為換行符int n; // 定義整數 n，表示數組長度
vector<int>arr; // 定義一個整型向量 arr，用于存儲數組元素
int q; // 定義整數 q，表示查詢次數
struct node {int l, r, index; // 定義結構體 node，包含三個整型變量 l, r 和 index
};
vector<node>readd; // 定義一個 node 類型的向量 readd，用于存儲查詢
map<int, int>arr_left; // 定義一個映射 arr_left，用于記錄元素上次出現的位置
class Tree {
public:vector<int>tree; // 定義一個整型向量 tree，用于樹狀數組int lowbit(int i) { // 返回 i 的最低位 1 的值return i & -i;}void sett(int i, int v) { // 在樹狀數組中更新值while (i < tree.size()) {tree[i] += v;i += lowbit(i);}}int gett(int i) { // 獲取前 i 項的和int ret = 0;while (i > 0) {ret += tree[i];i -= lowbit(i);}return ret;}int range(int l, int r) { // 獲取區間 [l, r] 的和return gett(r) - gett(l - 1);}
};
Tree t1; // 定義一個 Tree 類的對象 t1
void init() { // 初始化函數cin >> n; // 輸入數組長度arr.assign(n + 1, 0); // 將數組大小設為 n+1，并初始化為 0for (int i = 1; i <= n; i++) {cin >> arr[i]; // 輸入數組元素}readd.clear(); // 清空 readd 向量cin >> q; // 輸入查詢次數for (int i = 1; i <= q; i++) {int l, r;cin >> l >> r; // 輸入每個查詢的左右邊界readd.push_back({ l,r,i }); // 將查詢添加到 readd 向量中}
}
vector<int>ret; // 定義整型向量 ret，用于存儲結果
void solve() {sort(readd.begin(), readd.end(), [](const node& a, const node& b) { // 按照查詢的右邊界 r 進行排序return a.r < b.r;});ret.assign(q + 1, -1); // 將 ret 大小設為 q+1，并初始化為 -1t1.tree.assign(arr.size() + 1, 0); // 初始化樹狀數組arr_left.clear(); // 清空 arr_left 映射int i = 1;for (auto& xx : readd) {int l = xx.l, r = xx.r, index = xx.index; // 取出每個查詢的 l, r 和 indexwhile (i <= r) {if (arr_left.count(arr[i])) { // 如果元素已在 arr_left 中記錄過int index1 = arr_left[arr[i]]; // 取出上次出現的位置t1.sett(index1, -1); // 在樹狀數組中將該位置的值減 1}arr_left[arr[i]] = i; // 更新 arr_left 中該元素的最新位置t1.sett(i, 1); // 在樹狀數組中將當前元素位置的值加 1i++;}ret[index] = t1.range(l, r); // 計算區間 [l, r] 的和并存儲在 ret 中}for (int i = 1; i < ret.size(); i++) {cout << ret[i] << endl; // 輸出每個查詢的結果}}signed main() {ios::sync_with_stdio(0), cin.tie(), cout.tie(0); // 加速輸入輸出init(); // 調用初始化函數solve(); // 調用解決函數
}

結尾

最后，感謝您閱讀我的文章，希望這些內容能夠對您有所啟發和幫助。如果您有任何問題或想要分享您的觀點，請隨時在評論區留言。
同時，不要忘記訂閱我的博客以獲取更多有趣的內容。在未來的文章中，我將繼續探討這個話題的不同方面，為您呈現更多深度和見解。
謝謝您的支持，期待與您在下一篇文章中再次相遇！