本論文解決的問題

1. 量化數據價值（機器學習模型訓練中各個數據點的貢獻）

2. 避免數據價值受到其所處數據集的影響，使數據點的估值更加穩定、一致

變量假設

假設 D 表示一個在全集 Z 上的數據分布。對于監督學習問題，我們通常認為 Z = X × Y，其中 X 是特征空間的一個子集，Y 是輸出，它可以是離散的或連續的。

S 是從 D 中獨立同分布抽取的 k 個數據點的集合。

簡寫：[m]={1, …, m}，k ～ [m] 表示從 [m] 中均勻隨機抽取的樣本。

U 表示一個取值在 [0, 1] 上的潛在函數（potential function）或性能度量（performance metric）。在本文的背景下，認為 U 表示學習算法（learning algorithm）和評估指標（evaluation metric）。對于任何 S ? Z，U(S) 表示集合 S 的價值。

Data Shapley

? ( z ; U , B ) = 1 m ∑ k = 1 m ( m ? 1 k ? 1 ) ? 1 ∑ S ? B \ { z } ∣ S ∣ = k ? 1 ( U ( S ∪ { z } ) ? U ( S ) ) \phi(z ; U, B)=\frac{1}{m} \sum_{k=1}^m\binom{m-1}{k-1}^{-1} \sum_{\substack{S \subseteq B \backslash\{z\} \\|S|=k-1}}(U(S \cup\{z\})-U(S)) ?(z;U,B)=m1?k=1∑m?(k?1m?1?)?1S?B\{z}∣S∣=k?1?∑?(U(S∪{z})?U(S))

解釋如下：

• $?(z;U,B)$ ：表示數據點 $z$ 在數據集 $B$ 中的 data Shapley 值。
• $m$ ：數據集 $B$ 中數據點的總數。
• $U$ ：勢函數或性能度量，用于評估數據集的價值或模型的性能。
• $S$ ：數據集 $B$ 的任意子集，不包含點 $z$。
• $\left(\genfrac{}{}{0ex}{}{m?1}{k?1}\right)$ : 是從 $m?1$ 個數據點中選擇 $k?1$ 個數據點的組合數，作為權重。
• ∑ S ? B \ { z } ∣ S ∣ = k ? 1 \sum_{\substack{S \subseteq B \backslash\{z\} \\|S|=k-1}} ∑S?B\{z}∣S∣=k?1?? ：求和符號，表示遍歷所有可能的子集 $S$ ，這些子集是從 $B$ 中除去 $z$ 后剩余的數據點中選取 $k?1$ 個數據點形成的。

上式為 Data Shapley 值的定義，只是改變 Data Shapley: Equitable Valuation of Data for Machine Learning 中公式的形式。
? i = C ∑ S ? D ? { i } V ( S ∪ { i } ) ? V ( S ) ( n ? 1 ∣ S ∣ ) \phi_i=C \sum_{S \subseteq D-\{i\}} \frac{V(S \cup\{i\})-V(S)}{\left(\begin{array}{c}n-1 \\ |S|\end{array}\right)} ?i?=CS?D?{i}∑?(n?1∣S∣?)V(S∪{i})?V(S)?
計算差別體現在：D-Shapley 論文中每種 |S| 集合情況下，因為權重相同，所以先求和再乘上權重 $C_{n?1}^{k?1}$，然后求和，最后乘上 $1/m$?? 權重。Data Shapley 論文中，是對于每種 |S| 情況，計算邊際貢獻后，就乘上對應的兩個權重。

Distributional Shapley Value

Distributional Shapley Value 中數據點 $z$ 的數據價值為：

ν ( z ; U , D , m ) ? E B ～ D m ? 1 [ ? ( z ; U , B ∪ { z } ) ] \nu(z ; U, \mathcal{D}, m) \triangleq \underset{B \sim \mathcal{D}^{m-1}}{\mathbf{E}}[\phi(z ; U, B \cup\{z\})] ν(z;U,D,m)?B～Dm?1E?[?(z;U,B∪{z})]?

上式中的 ? ( z ; U , B ∪ { z } ) \phi(z ; U, B \cup\{z\}) ?(z;U,B∪{z}) 可視為一個隨機變量。其中，數據集 $B$ 為從分布 $D$ 中隨機抽取的，包含 𝑚?1 個數據點的數據集。因為每次抽樣會得到不同的數據集 $B$，從而導致 Data Shapley 值的不同結果，但是通過期望就能考慮所有可能的數據集的平均情況，求出數據點的價值。

下面的公式提供了 D-Shapley 值的一個等價表述。
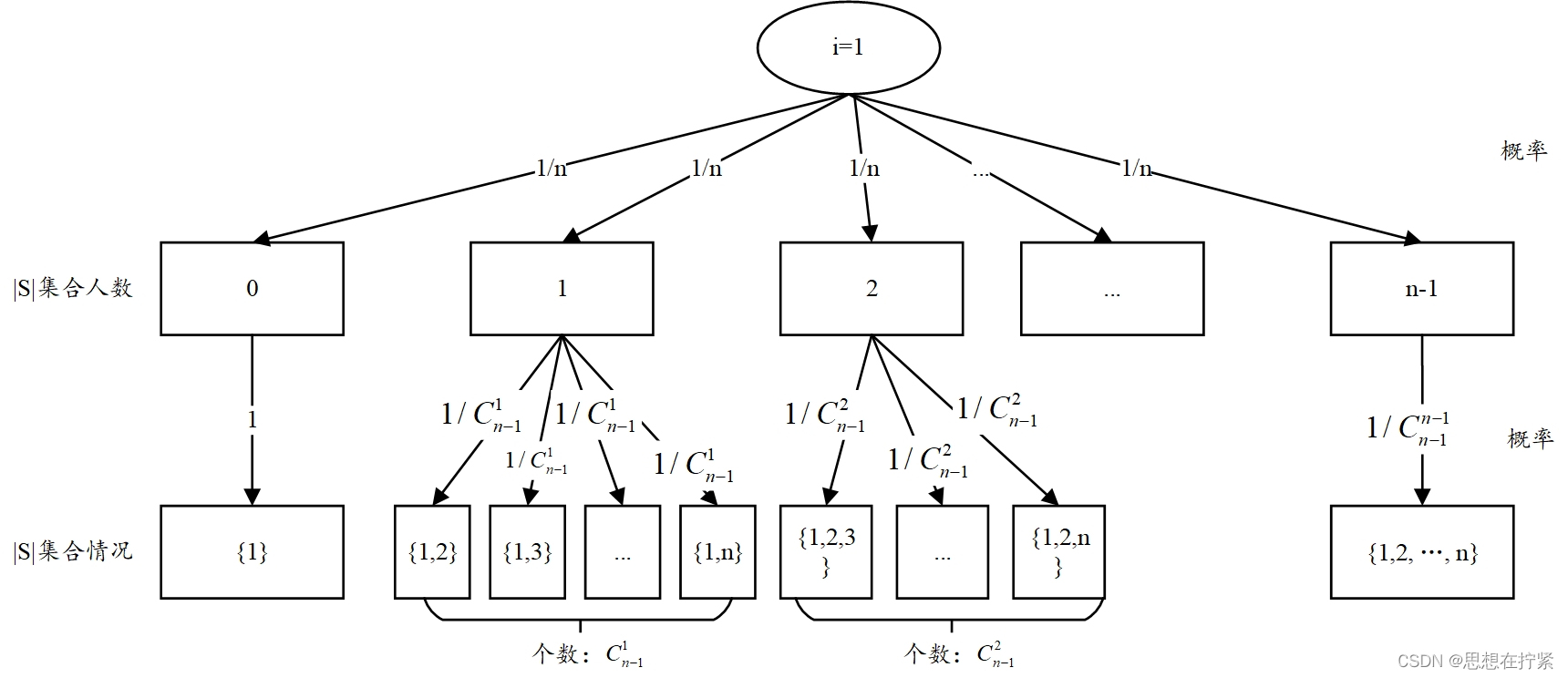
ν ( z ; U , D , m ) = E D ～ D m ? 1 [ ? ( z ; U , D ∪ { z } ) ] = E D ～ D m ? 1 [ 1 m ∑ k = 1 m 1 ( m ? 1 k ? 1 ) ∑ S ? D : ∣ S ∣ = k ? 1 ( U ( S ∪ { z } ) ? U ( S ) ) ] = 1 m ∑ k = 1 m 1 ( m ? 1 k ? 1 ) E D ～ D m ? 1 [ ∑ S ? D : ∣ S ∣ = k ? 1 ( U ( S ∪ { z } ) ? U ( S ) ) ] = 1 m ∑ k = 1 m E S ～ D k ? 1 [ U ( S ∪ { z } ) ? U ( S ) ] = E k ～ [ m ] S ～ D k ? 1 [ U ( S ∪ { z } ) ? U ( S ) ] \begin{aligned} & \nu(z ; U, \mathcal{D}, m)=\underset{D \sim \mathcal{D}^{m-1}}{\mathbf{E}}[\phi(z ; U, D \cup\{z\})] \\ & =\underset{D \sim \mathcal{D}^{m-1}}{\mathbf{E}}\left[\frac{1}{m} \sum_{k=1}^m \frac{1}{\binom{m-1}{k-1}} \sum_{\substack{S \subseteq D: \\ |S|=k-1}}(U(S \cup\{z\})-U(S))\right] \\ & =\frac{1}{m} \sum_{k=1}^m \frac{1}{\binom{m-1}{k-1}} \underset{D \sim \mathcal{D}^{m-1}}{\mathbf{E}}\left[\sum_{\substack{S \subseteq D: \\ |S|=k-1}}(U(S \cup\{z\})-U(S))\right] \\ & =\frac{1}{m} \sum_{k=1}^m \underset{S \sim \mathcal{D}^{k-1}}{\mathbf{E}}[U(S \cup\{z\})-U(S)] \\ & =\underset{\substack{k \sim[m] \\ S \sim \mathcal{D}^{k-1}}}{\mathbf{E}}[U(S \cup\{z\})-U(S)] \\ & \end{aligned} ?ν(z;U,D,m)=D～Dm?1E?[?(z;U,D∪{z})]=D～Dm?1E? ?m1?k=1∑m?(k?1m?1?)1?S?D:∣S∣=k?1?∑?(U(S∪{z})?U(S)) ?=m1?k=1∑m?(k?1m?1?)1?D～Dm?1E? ?S?D:∣S∣=k?1?∑?(U(S∪{z})?U(S)) ?=m1?k=1∑m?S～Dk?1E?[U(S∪{z})?U(S)]=k～[m]S～Dk?1?E?[U(S∪{z})?U(S)]?

首先 $k$ 是從集合 $[m]$ 中進行均勻隨機抽樣，然后對從分布 $D$ 中隨機抽取的 $k?1$ 個數據點構成的數據集 $S$，進行期望計算，最后得到的是添加數據點 $z$ 到 $S$ 后性能度量函數 $U$? 變化量的期望。