平衡二叉樹左旋右旋與紅黑樹

平衡二叉樹

定義

平衡二叉樹是二叉搜索樹的一種特殊形式。二叉搜索樹（Binary Search Tree，BST）是一種具有以下性質的二叉樹：

1. 對于樹中的每個節點，其左子樹中的所有節點都小于該節點的值。
2. 對于樹中的每個節點，其右子樹中的所有節點都大于該節點的值。
3. 左子樹和右子樹都必須是二叉搜索樹。

而平衡二叉樹（Balanced Binary Tree）在滿足了二叉搜索樹的所有性質的基礎上，還額外保證了樹的高度盡可能小，即任意節點的左右子樹高度差不超過1。

舉例

以下是平衡二叉樹的幾個例子：

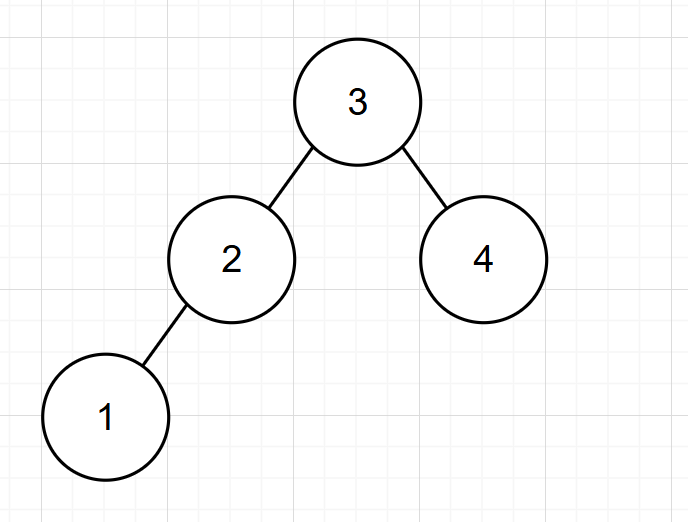
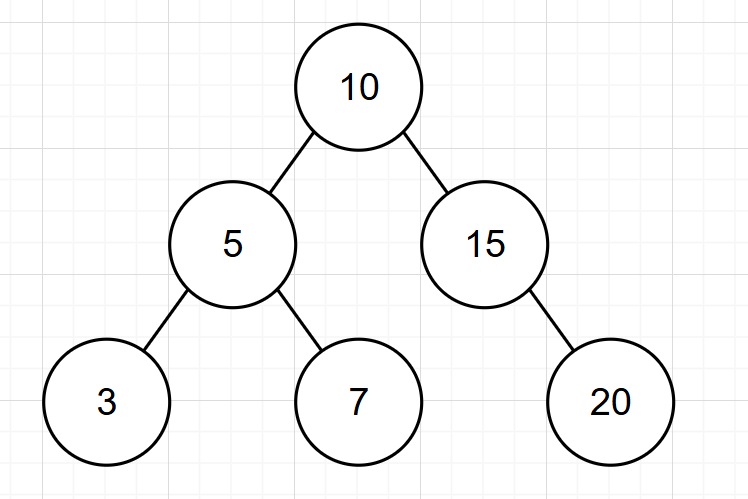
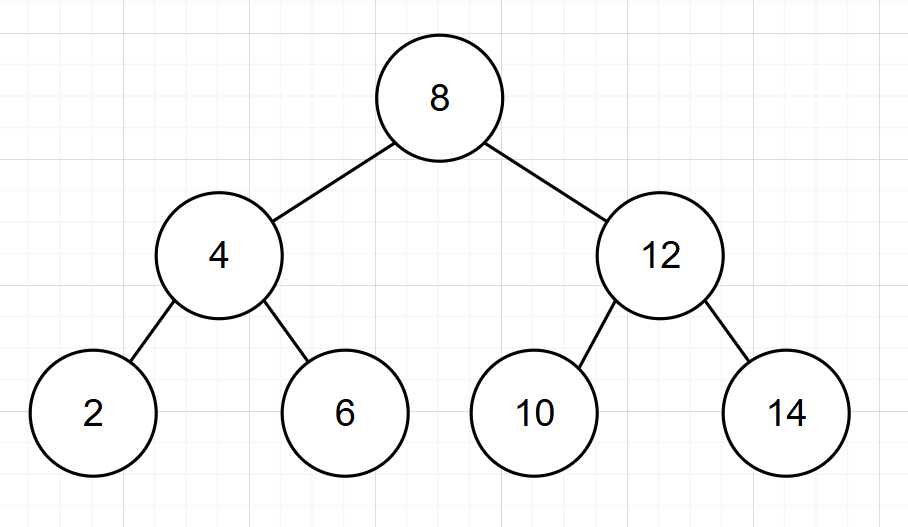
旋轉機制

平衡二叉樹通過旋轉操作來保持其平衡性。旋轉操作主要有兩種類型：左旋轉和右旋轉。這些旋轉操作通常應用于AVL樹和紅黑樹等平衡二叉樹的調整過程中。

左旋轉：左旋轉是一種操作，將一個節點的右子節點提升為新的根節點，原來的根節點成為新根節點的左子節點。左旋轉的目的是減小樹的整體高度，以維持平衡。

右旋轉：右旋轉是一種操作，將一個節點的左子節點提升為新的根節點，原來的根節點成為新根節點的右子節點。右旋轉的目的也是減小樹的整體高度，以維持平衡。

觸發時機：當添加一個節點之后，該樹不再是一顆平衡二叉樹

左旋

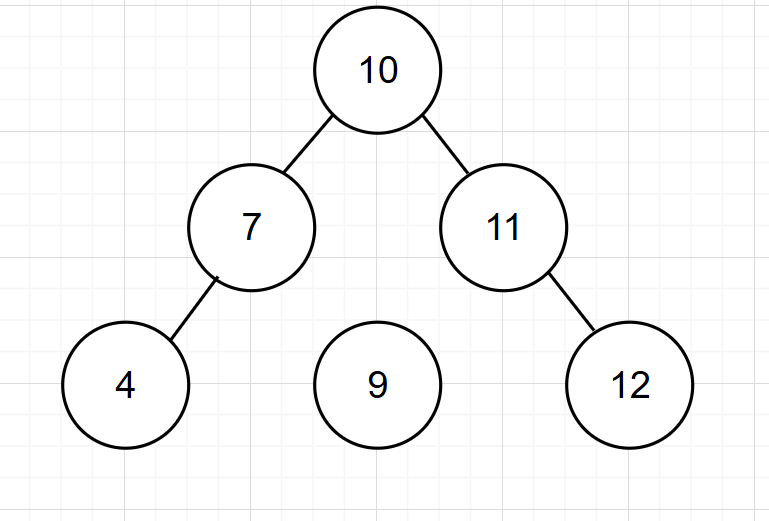
當我們想給

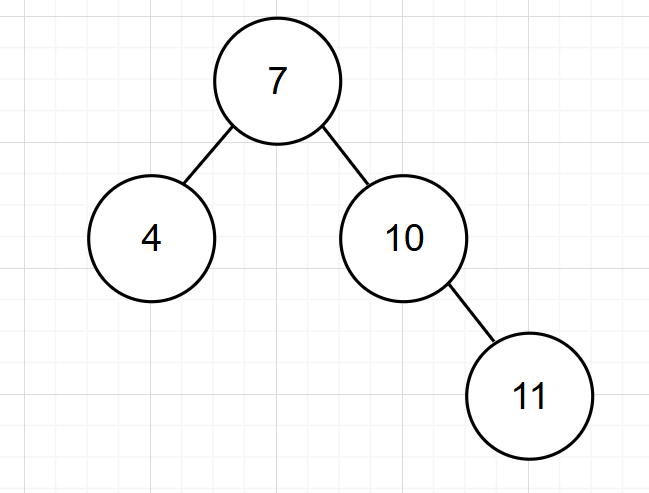
這個二叉樹中插入一個新的節點12，這個平衡二叉樹就會變為：

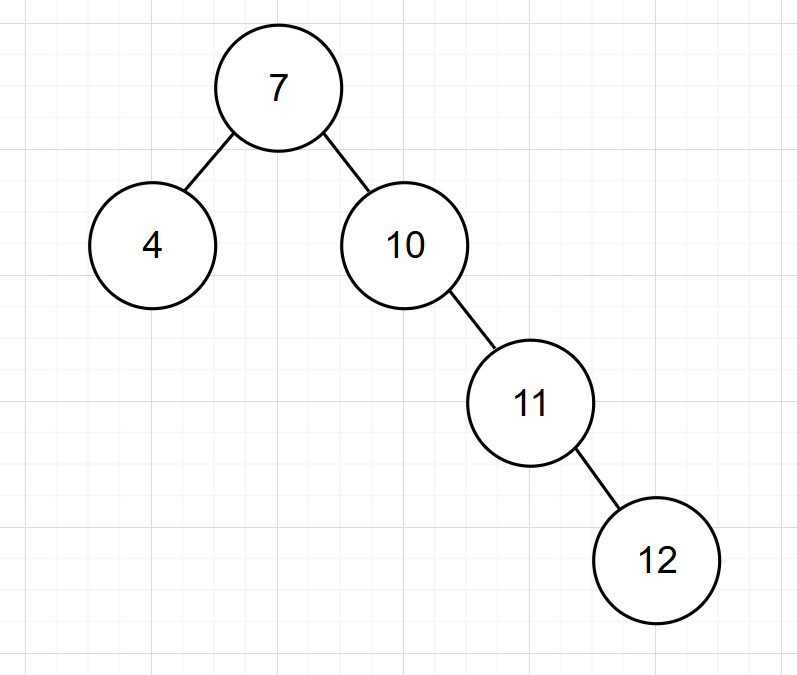
此時我們就會發現二叉樹不平衡了，為了重新平衡，我們就需要進行旋轉了。

為了進行旋轉，我們需要去尋找支點：從添加的節點開始，不斷的往父節點找不平衡的節點

這里我們從節點12開始往上找：

1. 節點11：平衡
2. 節點10：不平衡

所以節點10為支點！！

左旋的步驟：

1. 以不平衡的點作為支點
2. 把支點左旋降級，變成左子節點
3. 晉升原來的右子節點

旋轉后的二叉樹為：

---

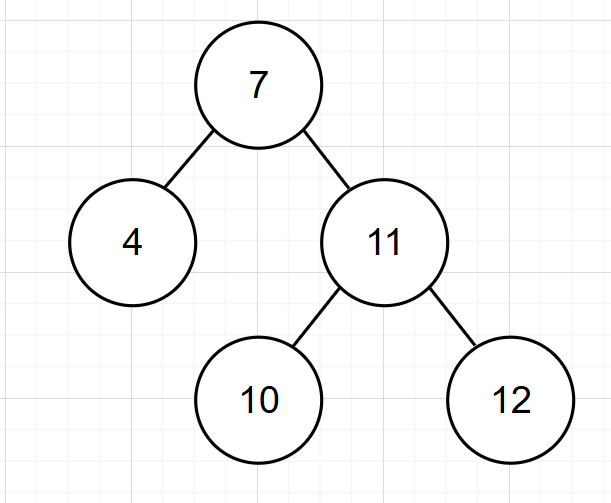
? 以上為較為簡單的左旋，下面為較為復雜的左旋

---

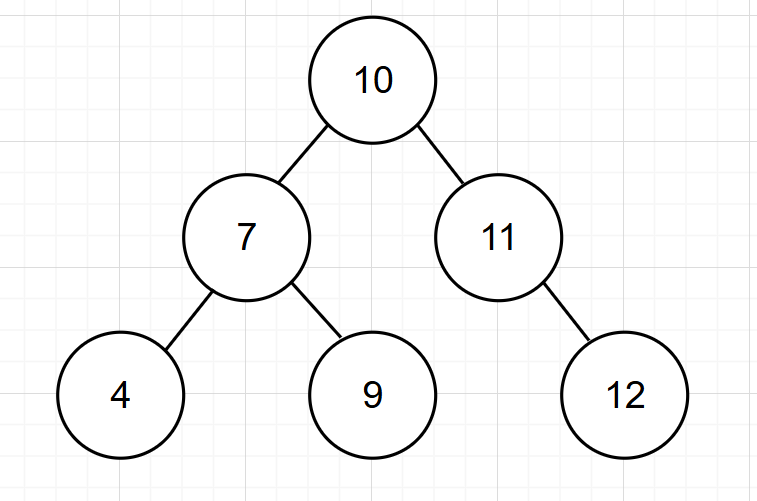
已知二叉樹（不平衡）：

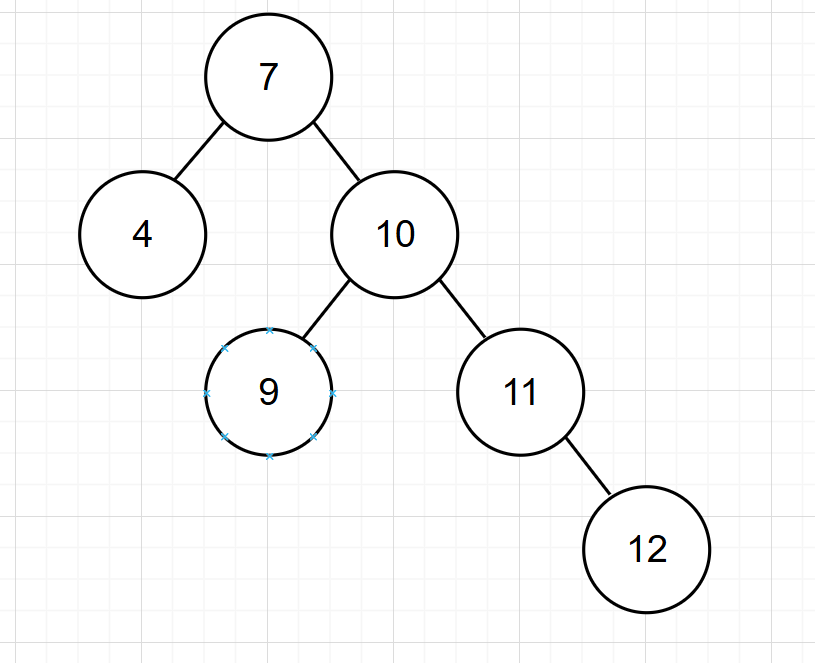
還是需要從添加的節點向上找不平衡的節點

1. 節點11：平衡
2. 節點10：平衡
3. 節點7：不平衡

節點7為支點

而此時旋轉的步驟和剛才的就有所不同了：

1. 以不平衡的點作為支點
2. 將根節點的右側往左拉
3. 原先的右子節點變成新的父節點，并把多余的左子節點出讓，給已經降級的根節點當右子節點

在上面的二叉樹中，多余的節點為節點9（節點9為節點10的左子結點很重要）。

下面為具體步驟：

1. 先將節點9（多余的左子節點）分離：

   

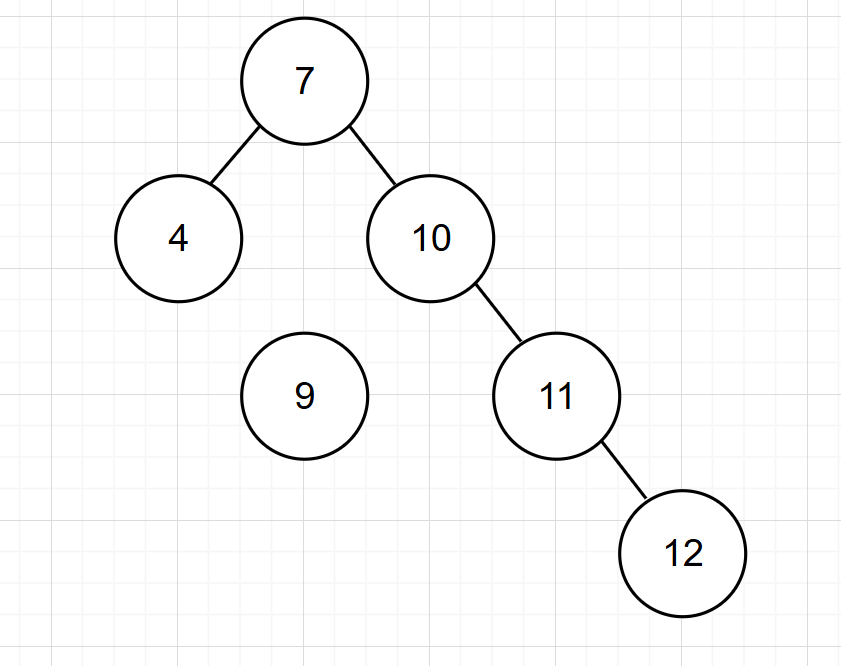
2. 以節點7為支點進行左旋：

   

3. 將多余的節點進行分配

   因為節點9之前為節點10的左子結點，所以此時9節點應該繼續接才節點10的左邊，此處應該放在節點7的右節點上

右旋

右旋與左旋在處理上是類似的，就不再粘貼圖示了

步驟

1. 以不平衡的點作為支點
2. 就是將根節點的左側往右拉
3. 原先的左子節點變成新的父節點，并把多余的右子節點出讓，給已經降級的根節點當左子節點

需要旋轉的四種情況

1.左左（一次右旋）

當根節點左子樹的左子樹有節點插入，導致二叉樹不平衡

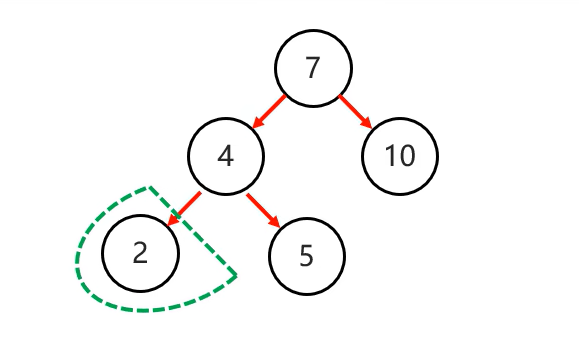
有兩種添加情況：

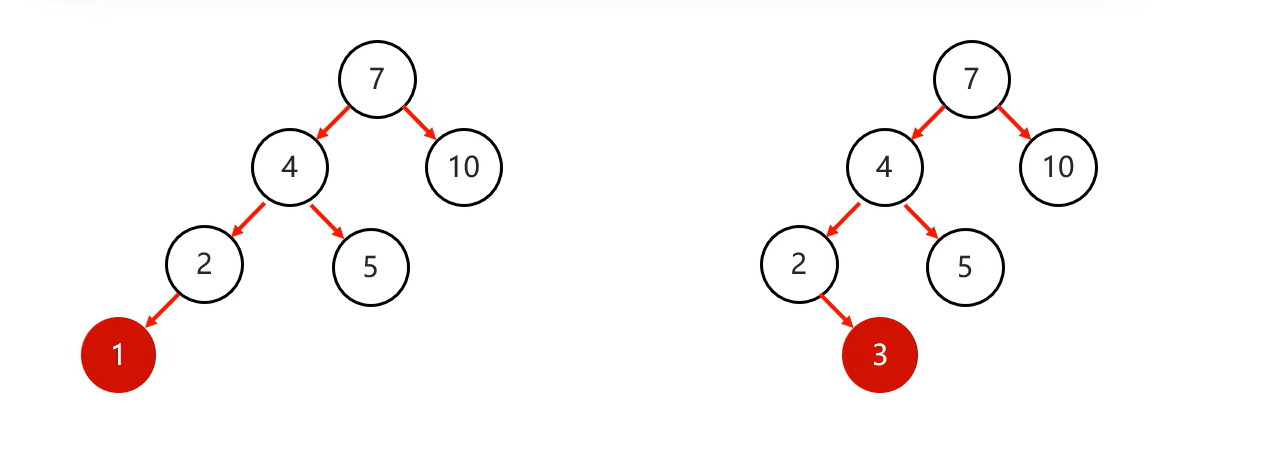
以節點7為根節點

我們只需要進行一次右旋就可以了：

2.左右（兩次旋轉）

當根節點左子樹的右子樹有節點插入，導致二叉樹不平衡

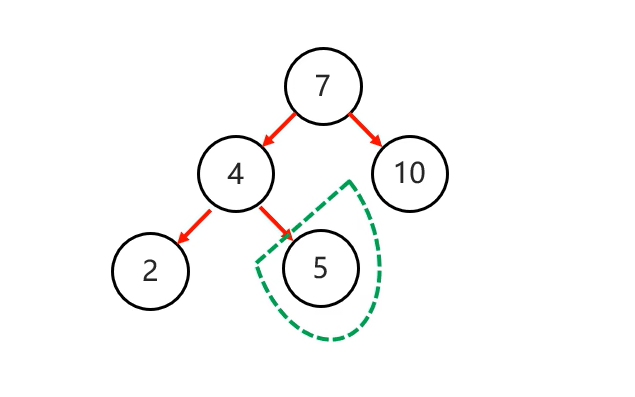
添加節點：

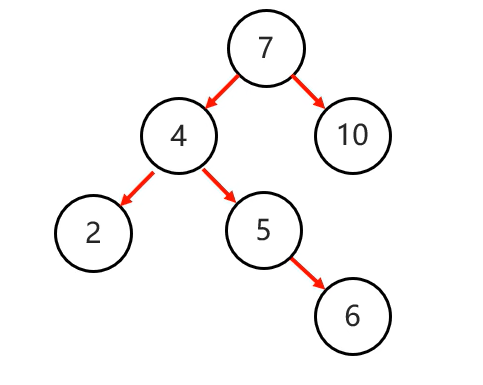
此時僅僅一次右旋就不能實現平衡了。

我們需要先一4為支點，先局部左旋，再整體右旋就可以實現了：

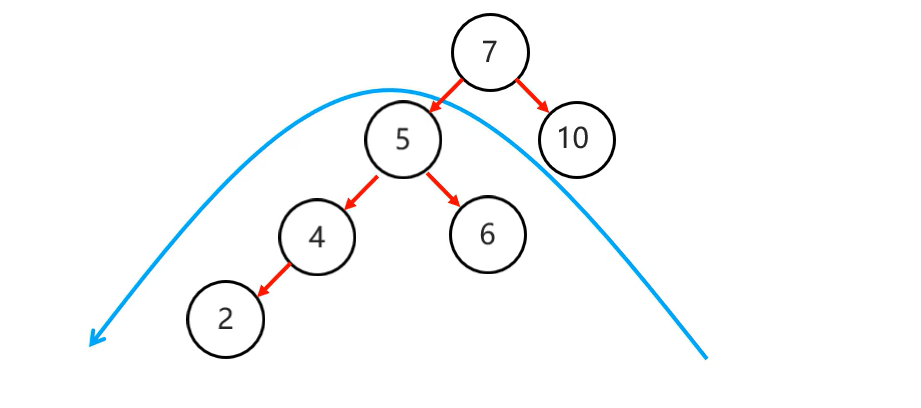
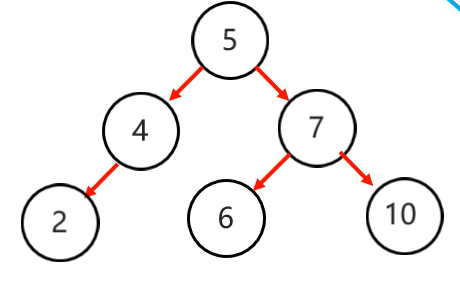
3.右右（一次旋轉）

當根節點右子樹的右子樹有節點插入，導致二叉樹不平衡

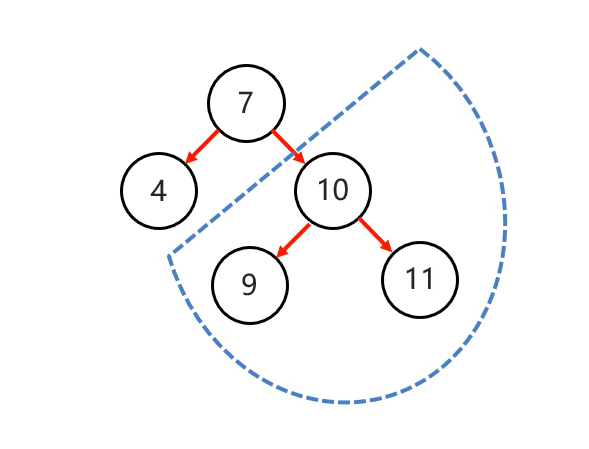
添加節點12：

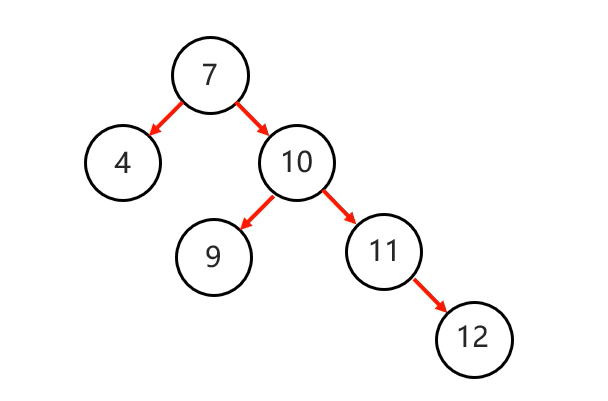
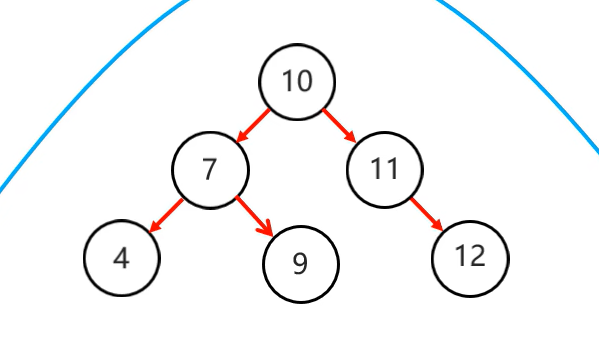
以節點7為支點進行左旋一次就能實現平衡：

4.右左（兩次旋轉）

當根節點右子樹的左子樹有節點插入，導致二叉樹不平衡

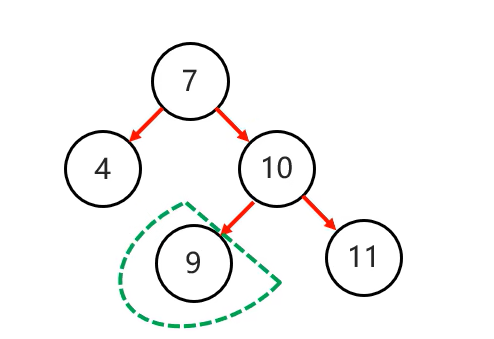
添加節點8：

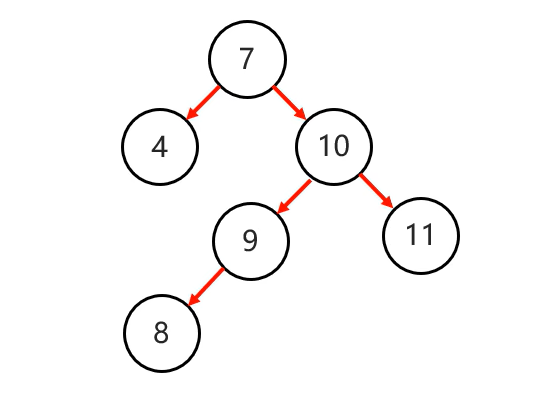
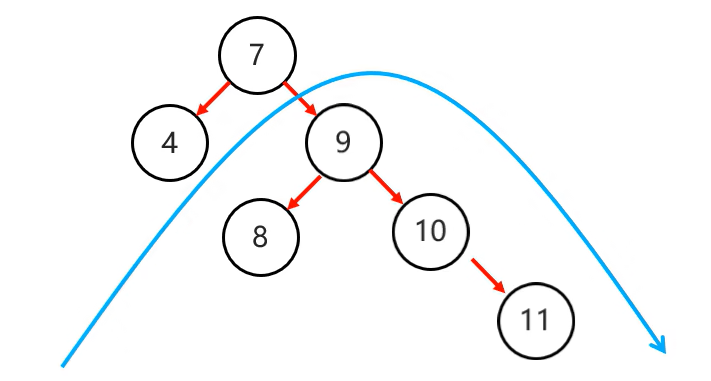
先局部右旋再整體左旋：

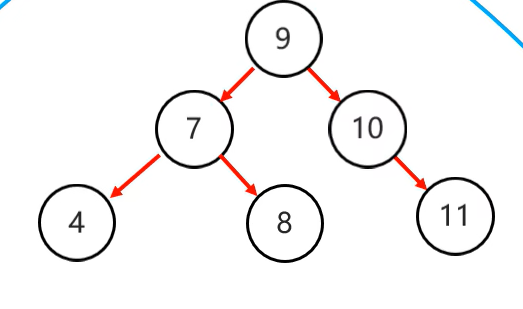
紅黑樹

• 紅黑樹是一種自平衡的二叉查找樹，是計算機科學中用到的一種數據結構。
• 1972年出現，當時被稱之為平衡二叉B樹。后來，1978年被修改為如今的"紅黑樹"
• 它是一種特殊的二叉查找樹，紅黑樹的每一個節點上都有存儲位表示節點的顏色
• 每一個節點可以是紅或者黑;紅黑樹不是高度平衡的，它的平衡是通過"紅黑規則"進行實現的

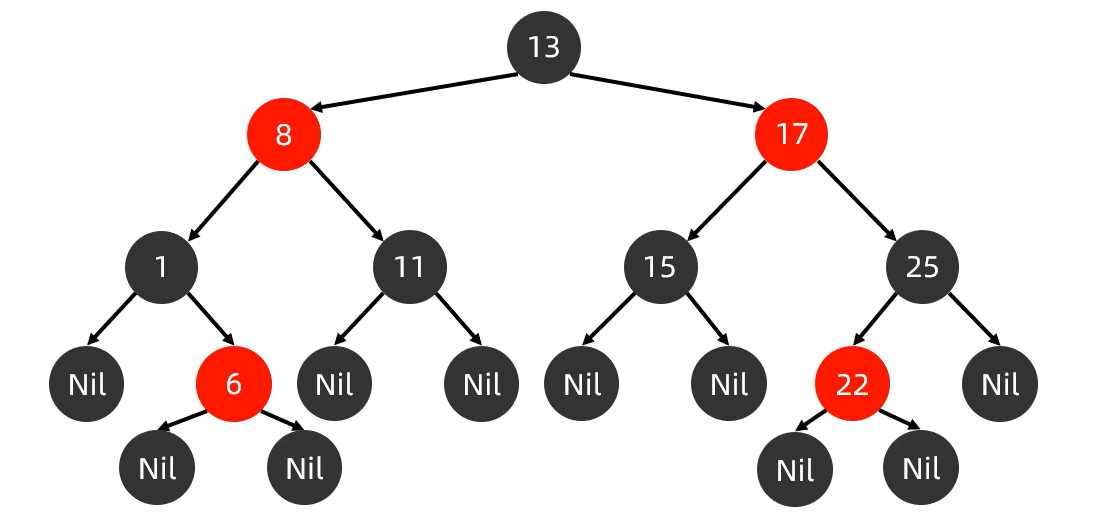
紅黑規則

1. 每一個節點或是紅色的，或者是黑色的
2. 根節點必須是黑色
3. 如果一個節點沒有子節點或者父節點，則該節點相應的指針屬性值為Nǐl，這些Nil視為葉節點，每個葉節點(Nil)是黑色的
4. 如果某一個節點是紅色，那么它的子節點必須是黑色(不能出現兩個紅色節點相連的情況)
5. 對每一個節點，從該節點到其所有后代葉節點的簡單路徑上，均包含相同數目的黑色節點

添加節點規則

默認顏色：添加節點默認是紅色的(效率高)

舉例

假設我們需要添加三個節點：20，18，23

1.假設三個節點都是黑色的

先添加節點20：

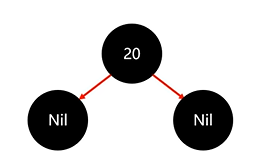
然后添加節點18：

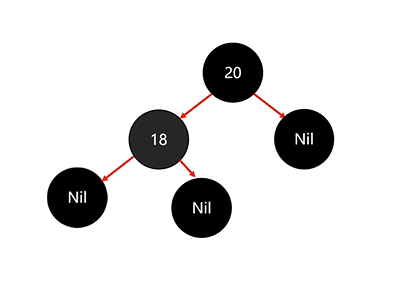
此時我們發現我們的紅黑樹已經違背了紅黑規則（第五條規則）

如果我們把節點18變為紅色，則就滿足了紅黑規則：

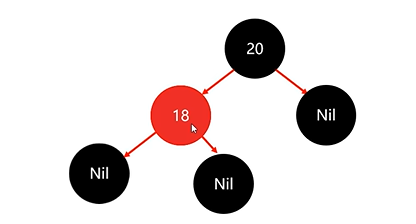
下來存節點23：

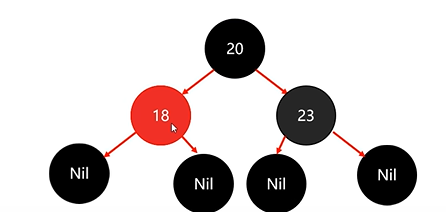
依舊違背紅黑規則，將23變為紅色：

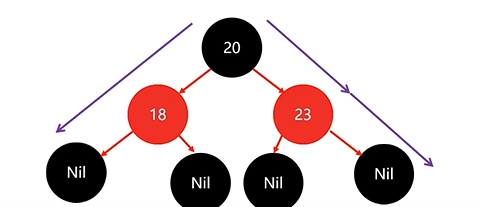
一共調整了兩次節點顏色

2.假設節點顏色都為紅色：

那么先添加節點20：

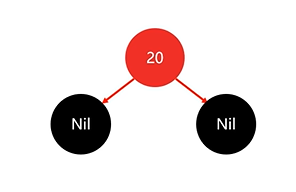
違背了規則2

將節點變為黑色后，插入節點18：

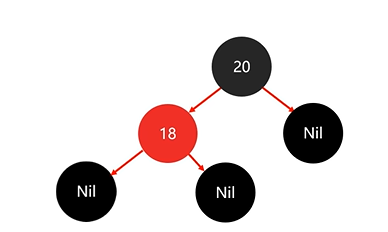
并沒有違背紅黑規則，不需要調整

下來添加節點23：

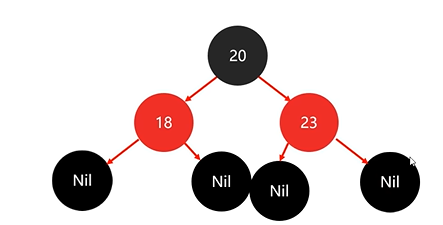
依然不需要調整。

一共調整了一次節點顏色

所以我們得出結論：默認顏色：添加節點默認是紅色的(效率高)

小結

本篇博客到這里就結束了，如果有錯誤麻煩大家指正，感謝閱讀！

已經到底啦！！！