????????要了解哈夫曼樹，可以先了解一下哈夫曼編碼，假設我們有幾個字母，他們的出現頻率是A: 1?B: 2?C: 3?D: 4?E: 5?F: 6 G: 7。那么如果想要壓縮數據的同時讓訪問更加快捷，就要讓頻率高的字母離根節點比較進，容易訪問，頻率低的離根節點遠。

所以，構建哈夫曼樹的步驟，是一直找最小頻率的兩個節點，組成一個樹，拿上面的例子：

A B的頻率最低，所以第一步先把AB當作左右孩子構建樹，現在AB相當于一個節點，權值為3。

再次比較，最小的權值是3，3（一個是AB節點的根，一個是C節點）接著構成樹。

現在最小的是權值為4，5節點，相當于4，5節點構成樹，但此時上面的樹仍然存在。

這里直接放最后樹的結果了：

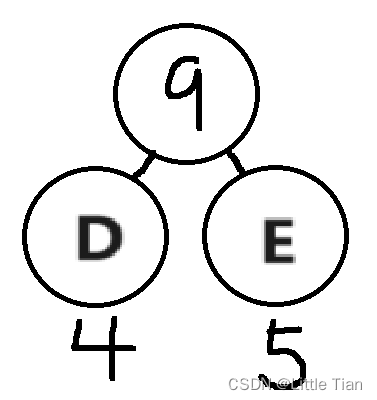
現在梳理一下步驟：

1.先找到最小的兩個點，構建他們的根節點。
2.把這兩個點從節點中去除，把他們的根節點加入進來。
3.循環這個過程直到只有一個節點。

????????首先我們要寫一個尋找權值最小并且構建根節點的函數，這里我們用一個數組用來存放普通的樹節點，根據數學推導，（會增加 n-1 個節點，因為最開始是2個節點增加一個）哈夫曼樹最后是 2n-1 個節點，這里先創建n個節點，后面可以realloc擴容。

????????哈夫曼樹的創建先創建 n?的節點的空間，給 n 個節點賦值，也就是初始值。這里的parent是告訴所有節點都在可比較的范圍內，如果parent為1，那么說明節點已經參與構建樹，也就是再尋找最小值時跳過。

typedef struct HuffmanTree {TreeNode* array;int length;
}HuffmanTree;HuffmanTree* HuffmanTreeInit(int length,int* data,HuffmanTree* H) {H = (HuffmanTree*)malloc(sizeof(HuffmanTree));H->array = (TreeNode*)malloc(sizeof(TreeNode) * length);H->length = length;for (int i = 0; i < length; i++) {H->array[i].val = data[i];H->array[i].lchild = NULL;H->array[i].rchild = NULL;H->array[i].parent = 0;}return H;
}

????????接著是尋找最小的兩個值的節點，index數組存放的是兩個節點的序號，最后返回，前后兩個for循環一樣，只不過要注意第二個for循環 && j!=index[0] ，為了找到第二個最小值，不和第一個重復。

int* FindTwoMin(HuffmanTree* H) {int* index = (int*)malloc(sizeof(int) * 2);int min1 = 1000;int min2 = 1000;for (int i = 0; i < H->length; i++) {if (H->array[i].parent == 0) {if (H->array[i].val < min1) {min1 = H->array[i].val;index[0] = i;}}}for (int j = 0; j < H->length; j++) {if (H->array[j].parent == 0) {if (H->array[j].val < min2 && j!=index[0]) {min2 = H->array[j].val;index[1] = j;}}}return index;
}

最后就是構建哈夫曼樹：

void CreatHuffmanTree(HuffmanTree* H) {int i = H->length,count=H->length;while( i < count * 2 - 1) {先找到最小的兩個節點的序號int* index = FindTwoMin(H);創建最小兩個節點的根H->array = (TreeNode*)realloc(H->array,sizeof(TreeNode) * (i + 1));H->array[i].val = H->array[index[0]].val + H->array[index[1]].val;H->array[i].parent = 0;H->array[i].lchild = &H->array[index[0]];H->array[i].rchild = &H->array[index[1]];把parent置為非0，表示已經構建H->array[index[0]].parent = i;H->array[index[1]].parent = i;樹的容量值更新H->length++;i++;}
}

????????最后是主函數和結果，最后用先序遍歷打印了一下哈夫曼樹，符合上面哈夫曼樹的圖。?

這就是文章的全部內容了，希望對你有所幫助，如有錯誤歡迎評論。