【第四節】C/C++數據結構之樹與二叉樹

目錄

一、基本概念與術語

二、樹的ADT

三、二叉樹的定義和術語

四、平衡二叉樹

4.1 解釋

4.2 相關經典操作

4.3 代碼展示

一、基本概念與術語

樹(Tree)是由一個或多個結點組成的有限集合T。其中:
1 有一個特定的結點，稱為該樹的根(root)結點；
2 每個樹都有且僅有一個特定的，稱為根(Root)的節點。

樹的常用術語：
1 當n>1時，其中每一個集合本身又是一棵樹，并且稱為根的子樹(SubTree)；
2 節點的子樹稱為該節點的子節點(Child)，相應的，該節點稱為子節點的父節點(Parent )；
3 同一個父節點的子節點之間稱為兄弟節點(Sibling)；
4 節點的層次(Level)從根節點開始定義，根為第一層，根的子節點為第二層，雙親在同一層的節點互為堂兄弟，樹中節點最大的層次稱為樹的深度或高度；
5 如果將樹中節點的各子樹看成從左到右是有次序的，不能互換的，則稱該樹為有序R樹，否則稱為無序樹；
6 如果有n顆互不相交的樹組成一個集合，則這個集合被稱之為森林。

二、樹的ADT

數據及關系:
?? ?具有相同數據類型的數據元素或結點的有限集合。樹T的二元組形式為：????????????????????????? ?
?? ??? ??? ?T＝（D，R）
?? ?其中D為樹T中結點的集合，R為樹中結點之間關系的集合。
?????????????????????????? D＝{Root}∪DF
?? ?其中，Root為樹T的根結點，DF為樹T的根Root的子樹集合。
???????????? ??? ??? ?R＝{<Root，ri>，i＝1，2，…，m}
?? ?其中，ri是樹T的根結點Root的子樹Ti的根結點。
操作:
?? ?Constructor：
?? ??? ?前提：已知根結點的數據元素之值。
?? ??? ?結果：創建一棵樹。
?? ?Getroot:
?? ??? ?前提：已知一棵樹。.
?? ??? ?結果：得到樹的根結點。
?? ?FirstChild：
?? ??? ?前提：已知樹中的某一指定結點 p。
?? ??? ?結果：得到結點 p 的第一個兒子結點。
?? ?NextChild：
?? ??? ?前提：已知樹中的某一指定結點 p 和它的一個兒子結點 u。
?? ??? ?結果：得到結點 p 的兒子結點 u 的下一個兄弟結點 v。

基本操作：

????????初始化一棵空樹;
????????創建一棵樹;
????????判斷空樹，為空返回True，否則返回False;
????????按照某特定順序遍歷一棵樹;
????????求樹的深度;
????????在樹中某特定位置插入結點;
????????在樹中某特定位置刪除結點;
????????求某結點的雙親結點；
????????銷毀樹;
????????等等;

三、二叉樹的定義和術語

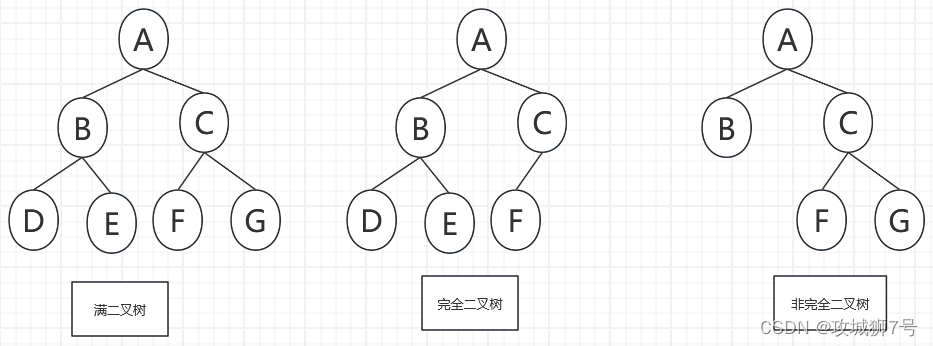
????????二叉樹(Tree)是n個節點的有限集合，該集合為空集(或稱為空二叉樹)，或者由一個根節點和兩顆互不相交的、分別稱為根節點的左子樹與右子樹的二叉樹組成。
A. 所有節點都只有左子樹的二叉樹叫左斜樹，所有節點都只有右子樹的二叉樹叫右斜樹，這兩者統稱為斜樹；
B. 在一棵二叉樹中，如果所有分支節點都存在左子樹與右子樹，并且所有葉子都在同一層次上，這樣的二叉樹稱為滿二叉樹；
C. 對一顆具有n個結點的二叉樹按層序編號，如果編號i(1<i<n)的節點與同樣深度的滿二叉樹中編號為i的結點在二叉樹中位置完全相同，則這顆二叉樹稱為完全叉樹。

四、平衡二叉樹

4.1 解釋

????????平衡二叉樹（Balanced Binary Tree），又稱為AVL樹（有別于AVL算法），是一種特殊的二叉搜索樹（Binary Search Tree）結構12。它具有以下性質：

  1. 它可以是空樹2。
  2. 它的左子樹和右子樹的高度差的絕對值不超過12。
  3. 它的左子樹和右子樹都是平衡二叉樹12。

????????平衡二叉樹的設計目的是為了解決普通二叉搜索樹在插入、刪除等操作時可能產生的不平衡問題，從而避免樹的高度過高，確保搜索效率始終保持在相對優化的水平。在平衡二叉樹中，查找、插入和刪除操作的時間復雜度都可以維持在O(logN)2。

平衡二叉樹在計算機科學中有廣泛的應用，例如：

  • 數據庫索引：用于加速數據庫的查詢操作3。
  • 查找和排序：可以快速查找和排序數據3。
  • 模擬實際問題：如航班預定系統中的座位分配3。
  • 實現字典或符號表：鍵是樹中的節點，值是與該鍵相關聯的數據，支持高效的查找、插入和刪除操作3。
  • 實現線性數據結構：如棧、隊列和優先隊列3。
  • 網絡路由：用于實現網絡路由表，進行快速的路由查找3。
  • 文件系統：用于實現文件系統的索引結構，支持快速的文件查找和訪問3。

????????總之，平衡二叉樹是一種高效的數據結構，它通過保持樹的平衡來優化搜索性能，并在各種應用中發揮著重要作用。

4.2 相關經典操作

????????平衡二叉樹（AVL樹）在插入或刪除節點后，可能會破壞其平衡性（即左右子樹的高度差超過1）。為了重新恢復平衡，需要進行旋轉操作。旋轉操作包括四種：左單旋、右單旋、左右旋和右左旋。下面我會逐一解釋這四種操作：

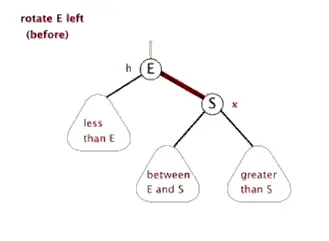
1. 左單旋：
????????當某個節點的左子樹的左子樹插入了一個新節點，導致該節點失去平衡時，需要進行左單旋。

步驟：

  • 以失去平衡的節點為根的子樹中，找到該節點左子樹的根節點（記作A）。
  • 將A節點提升為新的根節點。
  • 將原根節點變為A的右子樹。
  • A的左子樹保持不變。

左單旋的結果是將不平衡向右側轉移。

左單旋舉例：

????????針對節點8，它的左子樹的高度是1，右子樹的高度是3，高度差超過1.并且出錯的節點13和15均位于節點8的右子節點12的右邊，則通過左旋便可修復。

其一左單旋的結果：

動圖展示：

2. 右單旋：
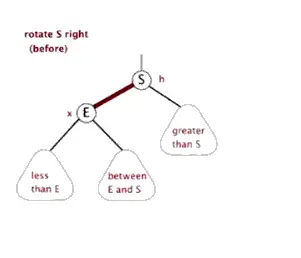
????????與左單旋對稱，當某個節點的右子樹的右子樹插入了一個新節點，導致該節點失去平衡時，需要進行右單旋。

步驟：

  • 以失去平衡的節點為根的子樹中，找到該節點右子樹的根節點（記作A）。
  • 將A節點提升為新的根節點。
  • 將原根節點變為A的左子樹。
  • A的右子樹保持不變。

右單旋的結果是將不平衡向左側轉移。

右單旋舉例：

????????針對節點8，它的左子樹的高度為3，右子樹高度為1，高度差超過1。并且出錯的節點1和3位于8節點的左子節點4的左邊。針對這種類型的非平衡樹，通過右旋便可以使其重新平衡。
具體做法： 將節點8作為節點4的右子節點，節點6作為節點8的左子節點

其一右單旋的結果：

用一個動圖來表示 右旋

3. 左右旋：
????????當某個節點的左子樹的右子樹插入了一個新節點，導致該節點失去平衡時，需要進行左右旋。

步驟：

  • 先對失去平衡的節點的左子樹進行右單旋。
  • 再對整棵樹進行左單旋。

????????左右旋實際上是右單旋和左單旋的組合，它首先嘗試將不平衡向右側轉移，然后再將不平衡向左側轉移。

左右旋舉例：

????????針對節點8，左子樹的高度是3，右子樹高度是1，高度差超過1。并且出錯的節點5和7均位于節點8的左節點4的右邊。這種情況需要先左旋再右旋便可恢復。

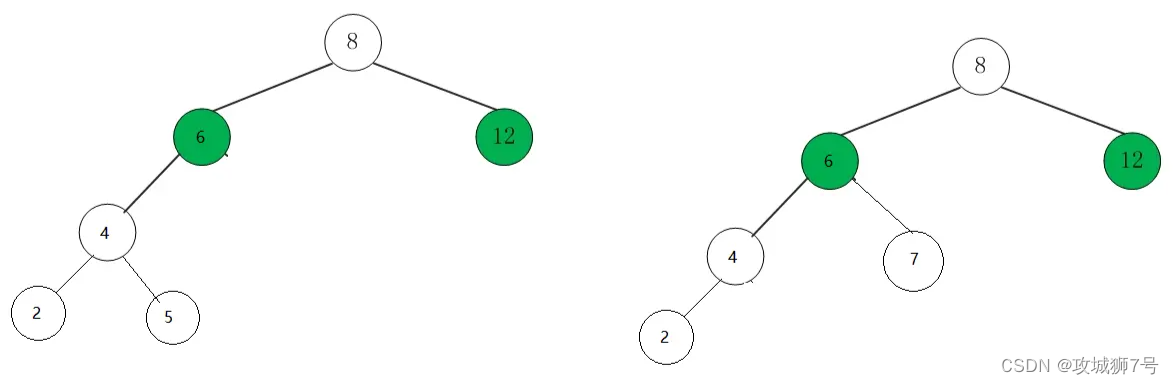
????????針對節點4進行左旋，左旋后變成了需要右旋的情況，可參考上面的右旋進行旋轉即可。

4. 右左旋：
????????與左右旋對稱，當某個節點的右子樹的左子樹插入了一個新節點，導致該節點失去平衡時，需要進行右左旋。

步驟：

  • 先對失去平衡的節點的右子樹進行左單旋。
  • 再對整棵樹進行右單旋。

????????右左旋實際上是左單旋和右單旋的組合，它首先嘗試將不平衡向左側轉移，然后再將不平衡向右側轉移。

????????這些旋轉操作確保了AVL樹在插入或刪除節點后仍然保持平衡，從而保證了樹的搜索效率。在進行旋轉操作時，還需要更新相關節點的高度信息，以便在后續操作中繼續檢查平衡性。

右左旋舉例：

類似的針對12節點先進行右旋，再整體左旋，原理類似 不再贅述

4.3 代碼展示

????????平衡二叉樹的左單旋，右單旋，左右旋，右左旋操作代碼演示

#include "Tree.h"CTree::CTree() :m_pRoot(0), m_nCount(0)
{
}CTree::~CTree()
{
}//************************************
// Method:    AddData 添加數據
// FullName:  CTree::AddData
// Access:    private 
// Returns:   bool
// Parameter: int nData
//************************************
bool CTree::AddData(int nData)
{return AddData(m_pRoot, nData);
}//************************************
// Method:    AddData
// FullName:  CTree::AddData
// Access:    private 
// Returns:   bool
// Parameter: PTREE_NODE & pTree 根節點
// Parameter: int nData
//************************************
bool CTree::AddData(TREE_NODE*& pTree, int nData)
{//pTree是否為空,如果為空說明有空位可以添加if (!pTree){pTree = new TREE_NODE{};pTree->nElement = nData;m_nCount++;return true;}//與根做對比，小的放在其左子樹，否則放在右子樹if (nData > pTree->nElement){AddData(pTree->pRChild, nData);//判斷是否平衡if (GetDeep(pTree->pRChild) - GetDeep(pTree->pLChild) == 2){//判斷如何旋轉if (pTree->pRChild->pRChild){//左旋LeftWhirl(pTree);}else if (pTree->pRChild->pLChild){//右左旋RightLeftWhirl(pTree);}}}if (nData < pTree->nElement){AddData(pTree->pLChild, nData);//判斷是否平衡if (GetDeep(pTree->pLChild) -GetDeep(pTree->pRChild) == 2){//判斷如何旋轉if (pTree->pLChild->pLChild){//右旋RightWhirl(pTree);}else if (pTree->pLChild->pLChild){//左右旋LeftRightWhirl(pTree);}}}
}//************************************
// Method:    DelData   刪除元素
// FullName:  CTree::DelData
// Access:    private 
// Returns:   bool
// Parameter: int nData
//************************************
bool CTree::DelData(int nData)
{return DelData(m_pRoot, nData);
}//************************************
// Method:    DelData
// FullName:  CTree::DelData
// Access:    private 
// Returns:   bool
// Parameter: PTREE_NODE & pTree 根節點
// Parameter: int nData
//************************************
bool CTree::DelData(PTREE_NODE& pTree, int nData)
{bool bRet = false;//判斷是否為空樹if (empty()){return false;}//開始遍歷要刪除的數據if (pTree->nElement == nData){//判斷是否為葉子節點，是就可以直接刪除，//不是則需要找代替if (!pTree->pLChild && !pTree->pRChild){delete pTree;pTree = nullptr;m_nCount--;return true;}//根據左右子樹的深度查找要替換的節點if (GetDeep(pTree->pLChild) >= GetDeep(pTree->pRChild)){PTREE_NODE pMax = GetMaxOfLeft(pTree->pLChild);pTree->nElement = pMax->nElement;DelData(pTree->pLChild, pMax->nElement);}else{PTREE_NODE pMin = GetMinOfRight(pTree->pRChild);pTree->nElement = pMin->nElement;DelData(pTree->pRChild, pMin->nElement);}}else if (nData > pTree->nElement){bRet = DelData(pTree->pRChild, nData);//判斷是否平衡if (GetDeep(pTree->pLChild) -GetDeep(pTree->pRChild) == 2){//判斷如何旋轉if (pTree->pLChild->pLChild){//右旋RightWhirl(pTree);}else if (pTree->pLChild->pLChild){//左右旋LeftRightWhirl(pTree);}}}else /*if (nData < pTree->nElement)*/{bRet = DelData(pTree->pLChild, nData);//判斷是否平衡if (GetDeep(pTree->pRChild) -GetDeep(pTree->pLChild) == 2){//判斷如何旋轉if (pTree->pRChild->pRChild){//左旋LeftWhirl(pTree);}else if (pTree->pRChild->pLChild){//右左旋RightLeftWhirl(pTree);}}}return bRet;
}//************************************
// Method:    ClearTree 清空元素
// FullName:  CTree::ClearTree
// Access:    private 
// Returns:   void
//************************************
void CTree::ClearTree()
{ClearTree(m_pRoot);m_nCount = 0;
}//************************************
// Method:    ClearTree
// FullName:  CTree::ClearTree
// Access:    private 
// Returns:   void
// Parameter: PTREE_NODE & pTree 根節點
//************************************
void CTree::ClearTree(PTREE_NODE& pTree)
{//從葉子節點開始刪除//刪除其左右子樹后再刪除根節點本身//判斷是否為空樹if (empty()){return;}//判斷是否為葉子節點if (!pTree->pLChild && !pTree->pRChild){delete pTree;pTree = nullptr;return;}ClearTree(pTree->pLChild);ClearTree(pTree->pRChild);ClearTree(pTree);
}//************************************
// Method:    TravsoualPre 前序遍歷
// FullName:  CTree::TravsoualPre
// Access:    private 
// Returns:   void
//************************************
void CTree::TravsoualPre()
{TravsoualPre(m_pRoot);
}//************************************
// Method:    TravsoualPre
// FullName:  CTree::TravsoualPre
// Access:    private 
// Returns:   void
// Parameter: PTREE_NODE pTree 根節點
//************************************
void CTree::TravsoualPre(PTREE_NODE pTree)
{//遞歸的返回條件if (!pTree){return;}//根左右printf("%d ", pTree->nElement);TravsoualPre(pTree->pLChild);TravsoualPre(pTree->pRChild);
}//************************************
// Method:    TravsoualMid  中序遍歷
// FullName:  CTree::TravsoualMid
// Access:    private 
// Returns:   void
//************************************
void CTree::TravsoualMid()
{TravsoualMid(m_pRoot);
}//************************************
// Method:    TravsoualMid
// FullName:  CTree::TravsoualMid
// Access:    private 
// Returns:   void
// Parameter: PTREE_NODE pTree 根節點
//************************************
void CTree::TravsoualMid(PTREE_NODE pTree)
{//遞歸的返回條件if (!pTree){return;}//左根右TravsoualMid(pTree->pLChild);printf("%d ", pTree->nElement);TravsoualMid(pTree->pRChild);
}//************************************
// Method:    TravsoualBack  后序遍歷
// FullName:  CTree::TravsoualBack
// Access:    private 
// Returns:   void
//************************************
void CTree::TravsoualBack()
{TravsoualBack(m_pRoot);
}//************************************
// Method:    TravsoualBack
// FullName:  CTree::TravsoualBack
// Access:    private 
// Returns:   void
// Parameter: PTREE_NODE pTree 根節點
//************************************
void CTree::TravsoualBack(PTREE_NODE pTree)
{//遞歸的返回條件if (!pTree){return;}//左右根TravsoualBack(pTree->pLChild);TravsoualBack(pTree->pRChild);printf("%d ", pTree->nElement);
}//************************************
// Method:    層序遍歷
// FullName:  CTree::LevelTravsoual
// Access:    public 
// Returns:   void
//************************************
void CTree::LevelTravsoual()
{vector<PTREE_NODE> vecRoot;  //保存根節點vector<PTREE_NODE> vecChild; //保存根節點的子節點vecRoot.push_back(m_pRoot);while (vecRoot.size()){for (int i = 0; i < vecRoot.size();i++){printf("%d ", vecRoot[i]->nElement);//判斷其是否左右子節點if (vecRoot[i]->pLChild){vecChild.push_back(vecRoot[i]->pLChild);}if (vecRoot[i]->pRChild){vecChild.push_back(vecRoot[i]->pRChild);}}vecRoot.clear();vecRoot = vecChild;vecChild.clear();printf("\n");}
}//************************************
// Method:    GetCount  獲取元素個數
// FullName:  CTree::GetCount
// Access:    public 
// Returns:   int
//************************************
int CTree::GetCount()
{return m_nCount;
}//************************************
// Method:    GetDeep 獲取節點深度
// FullName:  CTree::GetDeep
// Access:    private 
// Returns:   int
// Parameter: PTREE_NODE & pTree 
//************************************
int CTree::GetDeep(PTREE_NODE pTree)
{//判斷pTree是否為空if (!pTree){return 0;}int nL = GetDeep(pTree->pLChild);int nR = GetDeep(pTree->pRChild);//比較左右子樹的深度，取最大值加 1 返回return (nL >= nR ? nL : nR) + 1;
}//************************************
// Method:    GetMaxOfLeft 獲取左子樹中的最大值
// FullName:  CTree::GetMaxOfLeft
// Access:    private 
// Returns:   PTREE_NODE
// Parameter: PTREE_NODE pTree
//************************************
PTREE_NODE CTree::GetMaxOfLeft(PTREE_NODE pTree)
{//只要存在右子樹就有更大的值//是否空if (!pTree){return 0;}//判斷是否有右子樹while (pTree->pRChild){pTree = pTree->pRChild;}//返回最大值節點return pTree;
}//************************************
// Method:    GetMinOfRight 獲取右子樹中的最小值
// FullName:  CTree::GetMinOfRight
// Access:    private 
// Returns:   PTREE_NODE
// Parameter: PTREE_NODE pTree
//************************************
PTREE_NODE CTree::GetMinOfRight(PTREE_NODE pTree)
{//只要存在左子樹就有更小的值//是否空if (!pTree){return 0;}//判斷是否有右子樹while (pTree->pLChild){pTree = pTree->pLChild;}return pTree;
}//************************************
// Method:    LeftWhirl 左旋
// FullName:  CTree::LeftWhirl
// Access:    private 
// Returns:   void
// Parameter: PTREE_NODE & pTree
//************************************
void CTree::LeftWhirl(PTREE_NODE& pK2)
{
/*k2                  k1k1   ==>       k2    NX  N              X
*///保存k1PTREE_NODE pK1 = pK2->pRChild;//保存XpK2->pRChild = pK1->pLChild;//k2變成k1的左子樹pK1->pLChild = pK2;//k1變成k2pK2 = pK1;
}//************************************
// Method:    RightWhirl  右旋
// FullName:  CTree::RightWhirl
// Access:    private 
// Returns:   void
// Parameter: PTREE_NODE & pTree
//************************************
void CTree::RightWhirl(PTREE_NODE& pK2)
{
/*k2            k1k1     ==>    N    k2N  X               X
*///保存k1PTREE_NODE pK1 = pK2->pLChild;//保存XpK2->pLChild = pK1->pRChild;//k1的右子樹為k2pK1->pRChild = pK2;//k2為k1pK2 = pK1;
}//************************************
// Method:    LeftRightWhirl 左右旋
// FullName:  CTree::LeftRightWhirl
// Access:    private 
// Returns:   void
// Parameter: PTREE_NODE & pTree
//************************************
void CTree::LeftRightWhirl(PTREE_NODE& pK2)
{
/*k2               k2              Nk1     左旋       N       右旋  K1   K2N             k1 [x]             [x][x]     
*/LeftWhirl(pK2->pLChild);RightWhirl(pK2);
}//************************************
// Method:    RightLeftWhirl 右左旋
// FullName:  CTree::RightLeftWhirl
// Access:    private 
// Returns:   void
// Parameter: PTREE_NODE & pTree
//************************************
void CTree::RightLeftWhirl(PTREE_NODE& pK2)
{
/*k2               k2                   Nk1    右旋       N     左旋    k2     K1N               [x]  k1           [x][x]
*/RightWhirl(pK2->pRChild);LeftWhirl(pK2);
}bool CTree::empty()
{return m_pRoot == 0;
}

調用代碼：

#include "Tree.h"int main()
{CTree tree;tree.AddData(1);tree.AddData(2);tree.AddData(3);tree.AddData(4);tree.AddData(5);tree.AddData(6);tree.AddData(7);tree.AddData(8);tree.AddData(9);tree.AddData(10);tree.LevelTravsoual();tree.DelData(4);tree.LevelTravsoual();return 0;
}

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/web/24030.shtml
繁體地址，請注明出處：http://hk.pswp.cn/web/24030.shtml
英文地址，請注明出處：http://en.pswp.cn/web/24030.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！

相關文章

【Linux】進程2——管理概念，進程概念

【Linux】進程2——管理概念，進程概念

1.什么是管理&#xff1f; 那在還沒有學習進程之前&#xff0c;就問大家&#xff0c;操作系統是怎么管理進行進程管理的呢&#xff1f; 很簡單&#xff0c;先把進程描述起來&#xff0c;再把進程組織起來&#xff01; 我們拿大學為例子 最典型的管理者——校長最典型的被管理…
閱讀更多...
來自工業界的知識庫 RAG 服務(三)，FinGLM 競賽獲獎項目詳解

來自工業界的知識庫 RAG 服務(三)，FinGLM 競賽獲獎項目詳解

背景介紹 前面介紹過工業界的 RAG 服務 QAnything 和 RagFlow 的詳細設計&#xff0c;也介紹過來自學術界的 一些優化手段。 前一陣子剛好看到智譜組織的一個金融大模型比賽 FinGLM&#xff0c;主要做就是 RAG 服務的競賽&#xff0c;深入研究了其中的幾個獲獎作品&#xff…
閱讀更多...
Pyramid Vision Transformer, PVT（ICCV 2021）原理與代碼解讀

Pyramid Vision Transformer, PVT（ICCV 2021）原理與代碼解讀

paper&#xff1a;Pyramid Vision Transformer: A Versatile Backbone for Dense Prediction without Convolutions official implementation&#xff1a;GitHub - whai362/PVT: Official implementation of PVT series 存在的問題 現有的 Vision Transformer (ViT) 主要設計…
閱讀更多...
C++結合ffmpeg獲取聲音的分貝值

C++結合ffmpeg獲取聲音的分貝值

提示&#xff1a;文章寫完后&#xff0c;目錄可以自動生成&#xff0c;如何生成可參考右邊的幫助文檔 文章目錄 前言一、分貝是什么&#xff1f;1.功率量2.場量 二、實際操作1.分析wav文件2.讀取麥克風 總結 前言 最近面對一個需求&#xff0c;就是需要傳遞聲音文件到模型里推…
閱讀更多...
鏈表的回文結構OJ

鏈表的回文結構OJ

鏈表的回文結構_牛客題霸_牛客網對于一個鏈表&#xff0c;請設計一個時間復雜度為O(n),額外空間復雜度為O(1)的算法&#xff0c;判斷其是否為。題目來自【牛客題霸】https://www.nowcoder.com/practice/d281619e4b3e4a60a2cc66ea32855bfa?tpId49&&tqId29370&rp1&a…
閱讀更多...
CodeMeter助力Hilscher，推動實現全球智能制造連接解決方案

CodeMeter助力Hilscher，推動實現全球智能制造連接解決方案

Hilscher的旗艦店為開放工業4.0聯盟&#xff08;OI4&#xff09;社區提供了應用商店的便捷和開放性&#xff0c;將這一概念引入工業領域。該商店依托CodeMeter的許可證管理和加密保護&#xff0c;為工業用戶提供了豐富的應用和解決方案庫&#xff0c;滿足他們在車間自動化和連接…
閱讀更多...
2020年06月C語言二級真題

2020年06月C語言二級真題

計算矩陣邊緣元素之和 題目描述 輸入一個整數矩陣&#xff0c;計算位于矩陣邊緣的元素之和。 所謂矩陣邊緣的元素&#xff0c;就是第一行和最后一行的元素以及第一列和最后一列的元素。 輸入格式 第一行分別為矩陣的行數n和列數m&#xff0c;兩者之間以一個空格分開。 接下來輸…
閱讀更多...
WPF中讀取Excel文件的內容

WPF中讀取Excel文件的內容

演示效果 實現方案 1.首先導入需要的Dll(這部分可能需要你自己搜一下) Epplus.dll Excel.dll ICSharpCode.SharpZipLib.dll 2.在你的解決方案的的依賴項->添加引用->瀏覽->選擇1中的這幾個Dll點擊確定。(添加依賴) 3.然后看代碼內容 附上源碼 using Excel; usi…
閱讀更多...
計網復習資料

計網復習資料

一、選擇題&#xff08;每題2分&#xff0c;共40分&#xff09; 1. Internet 網絡本質上屬于&#xff08; &#xff09;網絡。 A.電路交換 B.報文交換 C.分組交換 D.虛電路 2.在 OSI 參考模型中,自下而上第一個提供端到端服務的是( )。 A.數據鏈路層 B.傳輸…
閱讀更多...
Thinkphp使用Elasticsearch查詢

Thinkphp使用Elasticsearch查詢

在Thinkphp中調用ES&#xff0c;如果自己手寫json格式的query肯定是很麻煩的。我這里使用的是ONGR ElasticsearchDSL 構建 ES 查詢。ongr ElasticsearchDSL 的開源項目地址&#xff1a;GitHub - ongr-io/ElasticsearchDSL: Query DSL library for Elasticsearch。ONGR Elastics…
閱讀更多...
100V 15A TO-252 N溝道MOS管 HC070N10L 惠海

100V 15A TO-252 N溝道MOS管 HC070N10L 惠海

MOS管的工作原理是基于在P型半導體與N型半導體之間形成的PN結&#xff0c;通過改變柵極電壓來調整溝道內載流子的數量&#xff0c;從而改變溝道電阻和源極與漏極之間的電流大小。由于MOS管具有輸入電阻高、噪聲小、功耗低等優點&#xff0c;它們在大規模和超大規模集成電路中得…
閱讀更多...
package.json中resolutions的使用場景

package.json中resolutions的使用場景

文章目錄 用途配置示例使用方法注意事項和peerDependencies有什么不同peerDependenciesresolutions 總結 ?創作者&#xff1a;全棧弄潮兒 &#x1f3e1; 個人主頁&#xff1a; 全棧弄潮兒的個人主頁 &#x1f3d9;? 個人社區&#xff0c;歡迎你的加入&#xff1a;全棧弄潮兒的…
閱讀更多...
git【工具軟件】分布式版本控制工具軟件

git【工具軟件】分布式版本控制工具軟件

一、Git 的介紹 git軟件的作用&#xff1a;管理軟件開發項目中的源代碼文件。 常用功能&#xff1a; 倉庫管理、文件管理、分支管理、標簽管理、遠程操作 功能指令&#xff1a; add&#xff0c;commit&#xff0c;log&#xff0c;branch&#xff0c;tag&#xff0c;remote…
閱讀更多...
Ubuntu Linux LTS 24.04 AMD64 桌面版安裝記錄

Ubuntu Linux LTS 24.04 AMD64 桌面版安裝記錄

下載iso aria2c -x 4 -s 12 "https://mirrors.tuna.tsinghua.edu.cn/ubuntu-releases/24.04/ubuntu-24.04-desktop-amd64.iso" "https://mirrors.163.com/ubuntu-releases/24.04/ubuntu-24.04-desktop-amd64.iso" "https://mirrors.zju.edu.cn/ubuntu…
閱讀更多...
[pyradiomics][python]pyradiomics所有whl文件下載地址匯總

[pyradiomics][python]pyradiomics所有whl文件下載地址匯總

源碼地址&#xff1a;https://github.com/AIM-Harvard/pyradiomics pyradiomics是一個開源的Python軟件包&#xff0c;專門用于從醫學影像中提取高通量的定量特征&#xff0c;這些特征被稱為影像組學(Radiomics)特征。以下是關于pyradiomics的詳細介紹&#xff1a; 一、基本概…
閱讀更多...
華為端云一體化開發 （起步1.0）（HarmonyOS學習第七課）

華為端云一體化開發 （起步1.0）（HarmonyOS學習第七課）

官方文獻&#xff1a; 為豐富HarmonyOS對云端開發的支持、實現端云聯動&#xff0c;DevEco Studio推出了云開發功能&#xff0c;開發者在創建工程時選擇云開發模板&#xff0c;即可在DevEco Studio內同時完成HarmonyOS應用/元服務的端側與云側開發&#xff0c;體驗端云一體化協…
閱讀更多...
大數據面試題第二期*6

大數據面試題第二期*6

題1、Namenode掛了怎么辦? 方法一&#xff1a;將SecondaryNameNode中數據拷貝到namenode存儲數據的目錄。 方法二&#xff1a;使用importCheckpoint選項啟動namenode守護進程&#xff0c;從而將SecondaryNameNode中數據拷貝到namenode目錄中。 題2、Hadoop 的namenode 宕機怎么…
閱讀更多...
論文代碼解讀STPGNN

論文代碼解讀STPGNN

1.前言 本次代碼文章來自于《2024-AAAI-Spatio-Temporal Pivotal Graph Neural Networks for Traffic Flow Forecasting》&#xff0c;基本模型結構如下圖所示&#xff1a; 文章講解視頻鏈接 代碼開源鏈接 接下來就開始代碼解讀了。 2.代碼解讀 class nconv(nn.Module):de…
閱讀更多...
NDIS Filter開發-網絡數據的傳輸

NDIS Filter開發-網絡數據的傳輸

和NIC小端口驅動不同的是&#xff0c;無需考慮網絡數據具體是如何傳輸的&#xff0c;只需要針對NBL進行處理即可。Filter驅動程序可以啟動發送請求和接收指示&#xff0c;或“過濾”其他驅動程序的請求和指示。Filter模塊堆疊在微型端口適配器上。 驅動程序堆棧中的Filter模塊…
閱讀更多...
谷粒商城實戰(033 業務-秒殺功能4-高并發問題解決方案sentinel 1)

谷粒商城實戰(033 業務-秒殺功能4-高并發問題解決方案sentinel 1)

Java項目《谷粒商城》架構師級Java項目實戰&#xff0c;對標阿里P6-P7&#xff0c;全網最強 總時長 104:45:00 共408P 此文章包含第326p-第p331的內容 關注的問題 sentinel&#xff08;哨兵&#xff09; sentinel來實現熔斷、降級、限流等操作 騰訊開源的tendis&#xff0c…
閱讀更多...
最新文章

Copyright @ 2022~2023