快速排序(Quick Sort)(C語言) 超詳細解析!!!

生活的本質是什么呢? 無非就是你要什么就不給你什么. 而生活的智慧是什么呢? 是給你什么就用好什么. ---馬斯克

索引

一. 前言
二. 快速排序的概念
三. 快速排序的實現
- 1. hoare
- 2. 挖坑法
- 3. 前后指針法
總結

正文開始

一. 前言

接上文, 前面我們了解了插入排序, 與優化版本希爾排序, 那么本篇博客將詳細介紹另外一種排序, 快速排序.

博客主頁: 酷酷學!!!

感謝關注~

二. 快速排序的概念

快速排序是Hoare于1962年提出的一種二叉樹結構的交換排序方法，

其基本思想為：

任取待排序元素序列中的某元素作為基準值，按照該排序碼將待排序集合分割成兩子序列，左子序列中所有元素均小于基準值，右子序列中所有元素均大于基準值，然后最左右子序列重復該過程，直到所有元素都排列在相應位置上為止。

三. 快速排序的實現

將區間按照基準值劃分為左右兩半部分的常見方式有三種版本

1. hoare

在這里插入圖片描述
如圖所示, 排序的思想為

第一步:
兩個下標, 一個從后往前走, 一個從前往后走, 然后定義一個基準值key, 下表為keyi,這里要注意要保證end先走, 才能讓最后相遇的位置小于keyi的位置, 因為end先走無非就兩種情況, 第一種, end找到了比key小的值, 停下來, 最后一次begin相遇end,交換相遇結點與key結點, 第二種情況, end相遇begin, 此時end沒有找到比keyi小的值, 然后最后一次與begin相遇, 此時begin的值為上一次交換后的值, 所以比keyi小.然后相遇與keyi交換位置, 此時6這個位置就排好了

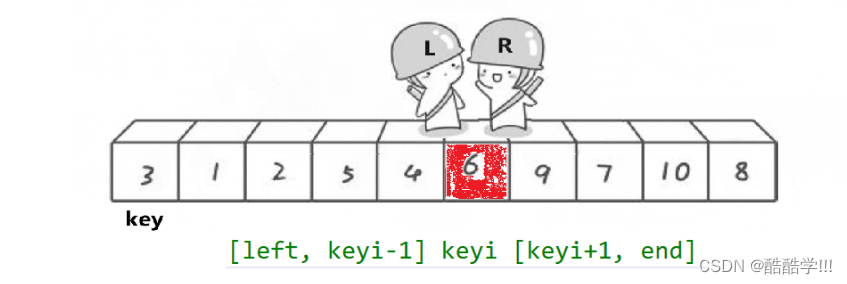
在這里插入圖片描述
第二步:

因為6這個位置排好了, 所以進行下一次的排序,以6劃分為兩個區域,然后再次遞歸調用函數, 如果最后的區間不存在或者只有一個值那么就結束函數.當left==right時此時區間只有一個值就不需要排序, 區間不存在也不需要排序.

void QuickSort(int* a, int left, int right)
{if (left >= right){return;}int keyi = left;int begin = left,end = right;while (begin < end){while (begin < end && a[end] >= a[keyi]){end--;}while (begin < end && a[begin] <= a[keyi]){begin++;}Swap(&a[begin], &a[end]);}Swap(&a[begin], &a[keyi]);keyi = begin;QuickSort(a, left, keyi - 1);QuickSort(a, keyi + 1, right);
}

我們來分析一下快速排序的時間復雜度, 目前來看, 每一層的時間復雜度為O(N), 高度為logn, 所以時間復雜度為O(NlogN), 但是這是在較好的情況下, 也就是相當于二叉樹, 左右區間差不多大, 那么如果是有序的一系列數字, 那么這個排序就很不友好, 很容易棧溢出,遞歸層次很深, 就不是logn, 那么如何進行優化呢, 就需要我們修改它的key值, 不大不小為最好的情況, 為了避免有序情況下，效率退化, 可以選擇 隨機選key法 或者 三數取中法

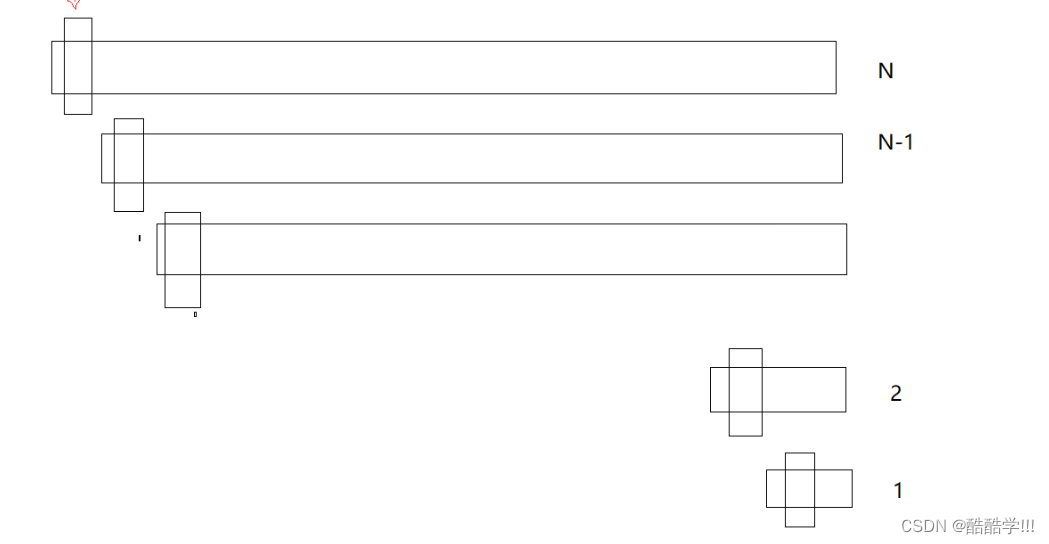
在這里插入圖片描述

這里我們來介紹一下三數取中法的優化.

int GetMidi(int* a, int left, int right)
{int midi = (right - left) / 2;if (a[left] < a[midi]){if (a[midi] < a[right]){return midi;}else if(a[left] < a[right]){return right;}else{return left;}}else//a[left] > a[midi]{if (a[left] < a[right]){return left;}else if (a[midi] > a[right]){return midi;}else{return right;}}
}

我們可以定義一個函數, 然后選取區間內最左邊的值, 最右邊的值, 中間的值,那個不大又不小的值作為key, 利用上述函數, 我們的代碼可以改寫為

void QuickSort(int* a, int left, int right)
{if (left >= right){return;}//三數取中int midi = GetMidi(a, left, right);Swap(&a[left], &a[midi]);int keyi = left;int begin = left,end = right;while (begin < end){while (begin < end && a[end] >= a[keyi]){end--;}while (begin < end && a[begin] <= a[keyi]){begin++;}Swap(&a[begin], &a[end]);}Swap(&a[begin], &a[keyi]);keyi = begin;QuickSort(a, left, keyi - 1);QuickSort(a, keyi + 1, right);
}

有了上述的優化, 我們的代碼效率就算在有序的情況下也能大大的提升效率, 但是還有一個問題, 我們知道, 二叉樹中遞歸調用, 最后一層遞歸調用的次數占據了總調用次數的一半, 我們可以把最后幾層的遞歸調用優化掉, 如果區間為十個數那么我們選擇其他的排序方法, 如果選堆排序, 十個數還需要建堆比較麻煩, 如果使用希爾排序, 那么就是多此一舉, 數據量不大選擇希爾排序屬實有點浪費了, 那我們就在時間復雜度為O(N^2)的排序中選擇一個相對來說效率比較高的插入排序.優化后的代碼如下:

void QuickSort(int* a, int left, int right)
{if (left >= right){return;}if ((right - left + 1) < 10){InsertSort(a + left, right - left + 1);}else{//三數取中int midi = GetMidi(a, left, right);Swap(&a[left], &a[midi]);int keyi = left;int begin = left, end = right;while (begin < end){while (begin < end && a[end] >= a[keyi]){end--;}while (begin < end && a[begin] <= a[keyi]){begin++;}Swap(&a[begin], &a[end]);}Swap(&a[begin], &a[keyi]);keyi = begin;QuickSort(a, left, keyi - 1);QuickSort(a, keyi + 1, right);}}

此優化在release版本下較為突出.

2. 挖坑法

前面單趟排序的方法由hoare發明之后又有另外的一種排序方法, 挖坑法, 它的思路比hoare排序的思想更容易理解

在這里插入圖片描述

//挖坑法
int PartSort3(int* a, int left, int right)
{//三數取中int midi = GetMidi(a, left, right);Swap(&a[left], &a[midi]);int keyi = left;int begin = left, end = right;int tmp = a[keyi];while (begin < end){while (begin < end && a[end] >= a[keyi]){end--;}a[keyi] = a[end];keyi = end;while (begin < end && a[begin] <= a[end]){begin++;}a[keyi] = a[begin];keyi = begin;}a[keyi] = tmp;return keyi;
}void QuickSort(int* a, int left, int right)
{if (left >= right){return;}if (right - left + 1 < 10){InsertSort(a + left, right - left + 1);}int keyi = PartSort3(a,left,right);QuickSort(a, left, keyi - 1);QuickSort(a, keyi + 1, right);
}

我們可以直接把單趟排序的算法拿出來封裝成一個函數, 如圖所示挖坑法特別好理解, 先讓keyi的值存放在一個臨時變量中, 挖一個坑,先讓對面的先走, 如果遇到比end小的就把它拿出來填入坑中, 然后begin在開始走, 遇到大的填入坑中, 這樣依次輪換,相遇時將keyi的值填入坑中.

3. 前后指針法

在這里插入圖片描述

如圖所示, 初始時, prev指針指向序列開頭, cur指針指向prev指針的后一個位置, 然后判斷cur指針指向的數據是否小于key, 則prev指針后移一位, 并于cur指針指向的內容交換, 然后cur++,cur指針指向的數據仍然小于key,步驟相同, 如果cur指針指向的數據大于key, 則繼續++,最后如果cur指針已經越界, 這時我們將prev指向的內容與key進行交換.

可以看到也就是一個不斷輪換的過程, 將大的數依次往后翻轉, 小的數往前挪動, 這種方法代碼寫起來簡潔, 當然我們也可以優化一下, 讓cur和prev相等時就沒必要進行交換

//前后指針版
int PartSort2(int* a, int left, int right)
{//三數取中int midi = GetMidi(a, left, right);Swap(&a[left], &a[midi]);int keyi = left;int prev = left;int cur = prev + 1;while (cur <= right){if (a[cur] < a[keyi] && prev++ != cur){Swap(&a[cur], &a[prev]);}cur++;}Swap(&a[prev], &a[keyi]);return prev;
}void QuickSort(int* a, int left, int right)
{if (left >= right){return;}if (right - left + 1 < 10){InsertSort(a + left, right - left + 1);}int keyi = PartSort2(a,left,right);QuickSort(a, left, keyi - 1);QuickSort(a, keyi + 1, right);
}

以上是遞歸版本的實現, 那么我們知道, 遞歸層次太深會容易棧溢出, 那么能不能采用非遞歸的實現呢, 答案肯定是可以的, 我們可以使用棧這個數據結果, 然后將區間入棧中, 棧不為空循環對區間進行排序, 一般linux系統下函數棧幀的空間的大小為8M, 而堆空間大小為2G, 所以這個空間是非常大的, 而且棧也是動態開辟的空間, 在堆區申請, 所以幾乎不需要考慮空間不夠, 我們可以將區間壓棧, 先壓入右區間, 在壓入左區間, 然后排序的時候先排完左區間再排右區間, 這是一種深度優先算法(DFS), 當然也可以創建隊列, 那么走的就是一層一層的排序, 每一層的左右區間都排序, 是一種廣度優先算法(BFS).
代碼實現:

這里可以創建一個結構體變量存放區間, 也可以直接壓入兩次, 分別把左值和右值壓入

//非遞歸版
#include"stack.h"
void QuickSortNonR(int* a, int left, int right)
{ST st;STInit(&st);STPush(&st, right);STPush(&st, left);while (!STEmpty(&st)){int begin = STTop(&st);STPop(&st);int end = STTop(&st);STPop(&st);int keyi = PartSort1(a, begin, end);//[begin,keyi-1] keyi [keyi+1,end]//先壓入右區間if (keyi + 1 < end){STPush(&st, end);STPush(&st, keyi + 1);}if (begin < keyi - 1){STPush(&st, keyi - 1);STPush(&st, begin);}}Destroy(&st);
}