數據結構——鏈式二叉樹知識點以及鏈式二叉樹數據操作函數詳解！！

引言：該博客將會詳細的講解二叉樹的三種遍歷方法：前序、中序、后序，也同時會講到關于二叉樹的數據操作函數。值得一提的是，這些函數幾乎都是建立在一個函數思想——遞歸之上的。這次的代碼其實寫起來十分簡單，用不了幾行就可以解決問題，但是其中的代碼思想和運作方式才是難點。但只要我們搞懂了思想，手撕代碼完全就沒問題了，就讓我們一起加油吧！

更多有關C語言和數據結構知識詳解可前往個人主頁：計信貓

一，二叉樹的遍歷方式

0，三序前言

1，前序

2，中序

3，后序

二，二叉樹的數據操作函數

1，二叉樹節點個數

2，二叉樹葉子節點個數

3，二叉樹高度?

4，二叉樹第k層節點個數

5，查找值為x的節點

6，二叉樹的銷毀

三，二叉樹的層序遍歷

1,? 層序遍歷

2，判斷完全二叉樹?

四，結語

一，二叉樹的遍歷方式

0，三序前言

? ? ? ? 其實我們所說的三序其實就可以分為前序、中序、后序，它們分別表示對一棵二叉樹不同的遍歷方式。我們在這里先對它們的遍歷方式做一次總結：

●前序：根，左子樹，右子樹

●中序：左子樹，根，右子樹

●后序：左子樹，右子樹，根

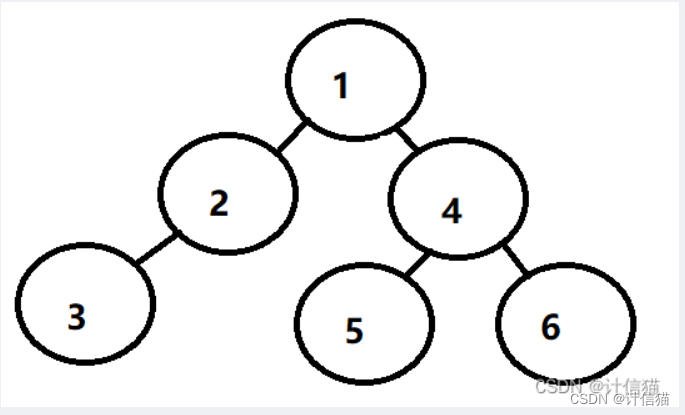
? ? ? ? 在這里，我們以如下的二叉樹為例子進行三序的介紹：

? ? ? ? 于是我們使用如下的代碼在VS中直接手搓出上圖的二叉樹，以方便我們后續對代碼的檢測。

typedef int BTDataType;
//二叉樹節點
typedef struct BinaryTreeNode
{BTDataType val;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;
//創建節點
BTNode* BuyNode(BTDataType x)
{BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));newnode->val = x;newnode->left = NULL;newnode->right = NULL;return newnode;
}
//創建二叉樹
BTNode* CreatBinaryTree()
{//創建節點BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);//將節點按照圖示連起來node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;//node1為根節點return node1;
}

? ? ? ? ?并且，我們仍然使用三文件操作法，如下圖所示：

1，前序

?●前序：根，左子樹，右子樹

? ? ? ? 那么對于該二叉樹，我們應該如何遍歷呢？

?????????按照前序遍歷的要求，我們就可以將一棵二叉樹不斷地劃分為根、左子樹、右子樹。

? ? ? ? 只有在我們將node1的左子樹遍歷完之后我們才可以進入右子樹。而node1的左子樹又可以被視作以node2為根，并且包含左右子樹的一棵新樹，所以我們又需要對新的樹進行前序遍歷。如此循環下去，其實遞歸的思想也就慢慢體現出來了。

? ? ? ? 所以，以上的樹被遍歷完之后的結果如下所示，其中N表示NULL空節點：

? ? ? ? ?所以前序遍歷的代碼如下：

//前序遍歷
void PreOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}printf("%d ", root->val);PreOrder(root->left);PreOrder(root->right);
}

2，中序

●中序：左子樹，根，右子樹

? ? ? ? 現在，我們以中序遍歷法遍歷如下二叉樹：

? ? ? ? 所以，我們還是將這棵二叉樹不斷地分解為根，左子樹，右子樹三個部分。但是我們這一次就會改變順序，我們需要先遍歷完左子樹后再進行根的遍歷，最后才進行右子樹的遍歷。而以node1為根節點的左子樹又可以繼續被細分為以上三個部分，所以我們又需要進行中序遍歷，直到某個節點的左子樹被遍歷完（為空），方可進行根的遍歷。

? ? ? ? 所以，以上的樹被中序遍歷完之后的結果如下：

? ? ? ? 所以中序遍歷的代碼入下：?

//中序遍歷
void MidOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}MidOrder(root->left);printf("%d ", root->val);MidOrder(root->right);
}

3，后序

●后序：左子樹，右子樹，根

? ? ? ? 如果我們使用后序遍歷法遍歷如下二叉樹，又會是怎樣一個結果呢？

? ? ? ? 所以我們仍然以之前學到的方式進行遞歸類推，先遍歷完node1的左子樹，后遍歷node1的右子樹，最后在遍歷根node1。而在遍歷node1的子樹時，它的子樹又可以被視為以node2或node4為根節點的新樹，故我們又對其再進行后序遍歷，直到遇到空節點。

? ? ? ? 所以我們模擬遍歷之后的結果如下圖所示：

? ? ? ? 那么，后序遍歷的代碼入下：

//后序遍歷
void BackOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}BackOrder(root->left);BackOrder(root->right);printf("%d ", root->val);
}

二，鏈式二叉樹的數據操作函數

1，二叉樹節點個數

? ? ? ? 當我們想要知道一棵二叉樹中有多少個節點的時候，我們就可以使用這個函數。

//求二叉樹中的節點個數
int TreeSize(BTNode* root);

? ? ? ? 在這個函數中，我們還是使用到了遞歸的思想。我們可以將一棵樹的總節點個數分為一個根節點與它的左右兩子樹的節點和。然后它的子樹又可以再次使用這個方法將它的子樹拆分，直到遇到NULL就遞歸結束，返回值為0。所以我們的代碼如下：

//求二叉樹中的節點個數
int TreeSize(BTNode* root)
{//遇到空，遞歸結束開始返回if (root == NULL){return 0;}//將二叉樹拆分為根和左右兩子樹之和return TreeSize(root->right) + TreeSize(root->left) + 1;
}

2，二叉樹葉子節點個數

? ? ? ? 這個函數用于求的一棵二叉樹之中的葉子節點的個數。

//求二叉樹中葉子節點的個數
int TreeLeafSize(BTNode* root)

?????????首先，我們可以確定的是，當一個節點的左右兩子節點全為NULL時，那么這個節點就是葉節點。而當我們想要找到一棵二叉樹中的葉節點個數時，我們就可以將總的葉節點的個數拆分為左右兩子樹的葉節點之和。然后我們不停以以上方式進行拆分，直到找到葉節點就遞歸結束，返回值為1。而要注意，空樹的葉節點個數為0，要特殊討論。所以按照以上的思想進行代碼實現如下：

//求二叉樹中葉子節點的個數
int TreeLeafSize(BTNode* root)
{//空樹沒有葉節點if (root == NULL){return 0;}//找到了葉節點，遞歸結束，返回1if (root->left == NULL && root->right == NULL){return 1;}//開始遞歸return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}

3，二叉樹高度?

? ? ? ? 二叉樹的高度其實就是二叉樹的度，也就是它的最大高度。

//求二叉樹的高度
int TreeHeight(BTNode* root);

? ? ? ? 當我們想要找到一棵樹的最大高度的時候，其實我們就可以將這棵樹的高度拆分為左子樹與右子樹中高度的較大值加上1（其中1代表了根也占一層高度）。如此遞歸下去，當我們遞歸到葉節點時，就遞歸結束，返回值為1。當然最后我們也需要注意，空樹的高度為0。所以我們的代碼如下：

//求二叉樹的高度
int TreeHeight(BTNode* root)
{//空樹高度為0if (root == NULL){return 0;}int left = TreeHeight(root->left);int right = TreeHeight(root->right);return left > right ? left + 1 : right + 1;
}

4，二叉樹第k層節點個數

? ? ? ? 該函數則專門用于求出一棵二叉樹中第k層的節點個數。

//求二叉樹第k層的節點個數
int TreeLevelKSize(BTNode* root, int k)；

? ? ? ? 對于這個函數的實現，還是請出我們的老朋友——遞歸。對于一棵二叉樹，求它第k層的節點個數時，我們就可以將這個問題視為求其根節點的左右子樹的（k-1）層的節點個數之和。直到k持續減一，使k==1時，說明該層就是我們的第k層，此時遞歸結束，返回值為1就可以了。?所以我們的代碼如下：

//求二叉樹第k層的節點個數
int TreeLevelKSize(BTNode* root, int k)
{//空樹則返回0if (root == NULL){return 0;}if (k == 1){return 1;}//根節點的左右子樹的（k-1）層的節點個數之和return TreeLevelKSize(root->left, k - 1) + TreeLevelKSize(root->right, k - 1);
}

5，查找值為x的節點

? ? ? ? 此函數用于查找二叉樹中值為x的節點，并返回該節點的地址。

//查找值為x的節點
BTNode* TreeFind(BTNode* root, BTDataType x);

? ? ? ? 既然我們想要找到值為x的節點時，那遍歷這個二叉樹就必不可少了！所以我們就可以使用之前學到的三序遍歷之一的前序遍歷法。我們先遍歷根，若根節點不是x節點我們就對它的左子樹進行遍歷，最后再對右子樹遍歷。若二叉樹為空或者不存在x節點我們都返回NULL。所以我們的代碼方法如下：

//查找值為x的節點
BTNode* TreeFind(BTNode* root, BTDataType x)
{//為空樹就返回NULLif (root == NULL){return NULL;}//先遍歷根節點if (root->val == x){return root;}//再遍歷左子樹BTNode* ret1 = TreeFind(root->left, x);if (ret1)//ret1不為空，說明x存在于左子樹{return  ret1;}BTNode* ret2 = TreeFind(root->right, x);if (ret2)//ret2不為空，說明x存在于右子樹{return ret2;}//整棵二叉樹都不存在x節點，返回NULLreturn NULL;
}

6，二叉樹的銷毀

? ? ? ? 當我們要結束對二叉樹的操作時，我們就需要對二叉樹進行銷毀操作，防止內存泄漏。

//二叉樹的銷毀
void TreeDestroy(BTNode* root);

? ? ? ? 在我們對二叉樹進行遍歷銷毀時，我們就應該選擇后序遍歷，將根節點進行最后銷毀，?因為一旦將根節點先行銷毀之后，那么我們就找不到根節點所對應的左右子樹了，就無法進行后續銷毀了。所以代碼如下：

//二叉樹的銷毀
void TreeDestroy(BTNode* root)
{if (root == NULL)//遇到空說明遍歷結束，開始返回{return;}TreeDestroy(root->left);TreeDestroy(root->right);free(root);
}

三，鏈式二叉樹的層序遍歷

1,? 層序遍歷

? ? ? ? 二叉樹的層序遍歷屬于廣度優先遍歷（BFS），而二叉樹的層序遍歷其實就是對二叉樹進行一層一層的遍歷，完成二叉樹的層序遍歷需要用到我們之前學到的隊列的知識。

? ? ? ? 現在我們對隊列進行一定的改裝。以前我們所學到的隊列中儲存的為int類型的值，而這時候我們將int改變為二叉樹節點的指針。經過以上操作之后，那么這個隊列里所儲存的就是二叉樹節點的指針了。

typedef struct BinaryTreeNode* QDataType;
//二叉樹的層序遍歷
void TreeLevelOrder(BTNode* root);

?????????我們現在以以下的二叉樹為例子：

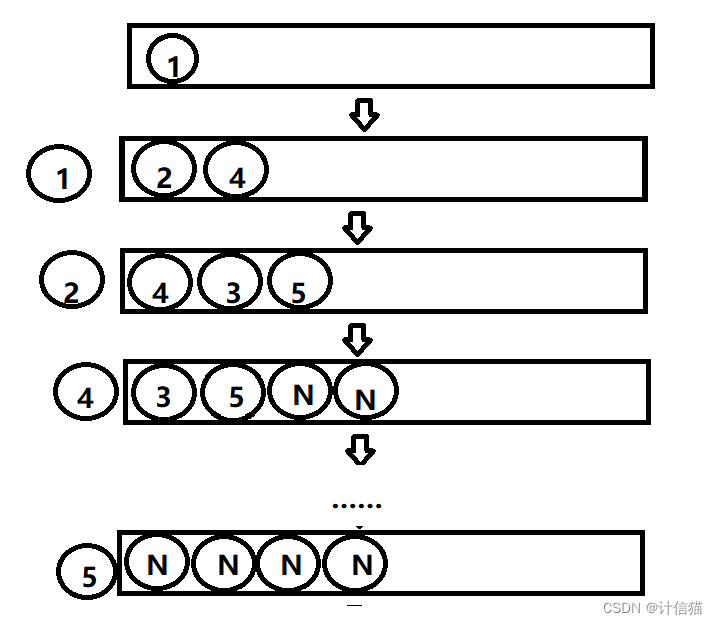
? ? ? ? 我們首先在隊列中插入根節點：

? ? ? ? 然后我們取出根節點，并且同時在隊列中加入其子節點2和4：

? ? ? ? 后我們取出節點2并且再次于隊列中加入節點2對應的子節點（空則不進入隊列）。

? ? ? ? 以此類推，直到當我們取出的節點為空時，那么此時對于這個二叉樹的層序遍歷就結束了。而在遍歷的過程中，我們始終遵循一個思想，就是上層帶下層。?所以在此思想的基礎之上，我們便可以寫出層序遍歷的代碼：

//二叉樹的層序遍歷
void TreeLevelOrder(BTNode* root)
{assert(root);//創建一個隊列Queue q;//初始化隊列QueueInit(&q);//向隊列中插入第一個元素QueuePush(&q, root);while (!QueueEmpty(&q)){//取出隊首節點并且打印BTNode* front = QueueFront(&q);QueuePop(&q);printf("%d ", front->val);//加入隊首節點的非空子節點if (front->left){QueuePush(&q, front->left);}if (front->right){QueuePush(&q, front->right);}}
}

2，判斷完全二叉樹?

? ? ? ? 當我們需要判斷一棵樹是否為完全二叉樹時我們就可以使用該函數，它的返回值為布爾類型。

//完全二叉樹的判斷
bool TreeComplete(BTNode* root);

? ? ? ? 在寫該函數時，我們則會用到以下的思路：

1，層序遍歷這個二叉樹，并且空指針也進入隊列

2，取出隊首節點遇到第一個空節點時，就開始進行判斷，如果隊列里面節點全為空就為完全二叉樹，后面有非空節點就不為完全二叉樹

? ? ? ? 讓我們結合下列的例子進行理解：

? ? ? ? 我們以之前我們學到的層序遍歷法來遍歷這個二叉樹，如下圖所示：

? ? ? ? 現在就是我們取出第一個空節點的時候，此時我們就對隊列里的元素進行判斷，如果隊列里邊全為空指針，那么這個二叉樹就為完全二叉樹，否則就不為完全二叉樹。而由我們的例子可見，該二叉樹就為完全二叉樹。?

? ? ? ? 所以我們就可以將此方法轉變為如下的代碼：

//完全二叉樹的判斷
bool TreeComplete(BTNode* root)
{assert(root);//創建一個隊列Queue q;//初始化隊列QueueInit(&q);//向隊列中插入第一個元素QueuePush(&q, root);while (!QueueEmpty(&q)){//取出隊首節點BTNode* front = QueueFront(&q);QueuePop(&q);//若取出的節點為空，就跳出循環，并對隊列中的節點進行判空if (front == NULL){break;}//不管是否為空，節點的子節點都加入隊列QueuePush(&q, front->left);QueuePush(&q, front->right);}//判斷隊列中的節點while (!QueueEmpty(&q)){//取出隊首節點BTNode* front = QueueFront(&q);QueuePop(&q);//隊列中有節點不為空，則不為完全二叉樹if (front != NULL){QueueDestroy(&q);return false;}}QueueDestroy(&q);return true;
}