1、樸素貝葉斯

貝葉斯分類法是基于貝葉斯定理的統計學分類方法。它通過預測一組給定樣本屬于一個特定類的概率來進行分類。貝葉斯分類在機器學習知識結構中的位置如下：

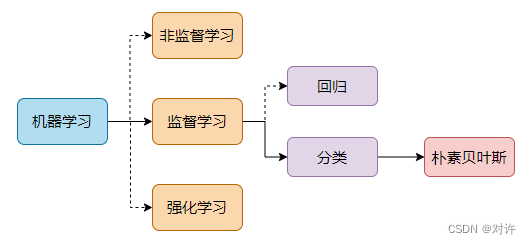
1.1、貝葉斯分類

貝葉斯分類的歷史可以追溯到18世紀，當時英國統計學家托馬斯·貝葉斯發展了貝葉斯定理，這個定理為統計決策提供了理論基礎。不過，貝葉斯分類得到廣泛實際應用是在20世紀80年代，當時計算機技術的進步使得大規模數據處理成為可能

在眾多機器學習分類算法中，貝葉斯分類和其他絕大多數分類算法都不同

例如，KNN、邏輯回歸、決策樹等模型都是判別方法，也就是直接學習出輸出Y和特征X之間的關系，即決策函數$Y$=$f(X)$或決策函數$Y$=$P(Y|X)$

但是，貝葉斯是生成方法，它直接找出輸出Y和特征X的聯合分布$P(X,Y)$，進而通過$P(Y|X)$=$\frac{P(X,Y)}{P(X)}$計算得出結果判定

貝葉斯分類是一類分類算法的總稱，這類算法均以貝葉斯定理為基礎，故統稱為貝葉斯分類。而樸素貝葉斯（Naive Bayes）分類是貝葉斯分類中最簡單，也是常見的一種分類方法

樸素貝葉斯算法的核心思想是通過特征考察標簽概率來預測分類，即對于給定的待分類樣本，求解在此樣本出現的條件下各個類別出現的概率，哪個最大，就認為此待分類樣本屬于哪個類別

例如，基于屬性和概率原則挑選西瓜，根據經驗，敲擊聲清脆說明西瓜還不夠成熟，敲擊聲沉悶說明西瓜成熟度好，更甜更好吃。所以，壞瓜的敲擊聲是清脆的概率更大，好瓜的敲擊聲是沉悶的概率更大。當然這并不絕對——我們千挑萬選的沉悶瓜也可能并沒熟，這就是噪聲了。當然，在實際生活中，除了敲擊聲，我們還有其他可能特征來幫助判斷，例如色澤、根蒂、品類等

樸素貝葉斯把類似敲擊聲這樣的特征概率化，構成一個西瓜的品質向量以及對應的好瓜/壞瓜標簽，訓練出一個標準的基于統計概率的好壞瓜模型，這些模型都是各個特征概率構成的。這樣，在面對未知品質的西瓜時，我們迅速獲取了特征，分別輸入好瓜模型和壞瓜模型，得到兩個概率值。如果壞瓜模型輸出的概率值更大一些，那這個瓜很有可能就是個壞瓜

1.2、貝葉斯定理

貝葉斯定理（Bayes Theorem）也稱貝葉斯公式，其中很重要的概念是先驗概率、后驗概率和條件概率

1.2.1、先驗概率

先驗概率是指事件發生前的預判概率。可以是基于歷史數據的統計，可以由背景常識得出，也可以是人的主觀觀點給出。一般都是單獨事件概率

例如，如果我們對西瓜的色澤、根蒂和紋理等特征一無所知，按照常理來說，好瓜的敲聲是沉悶的概率更大，假設是60%，那么這個概率就被稱為先驗概率

1.2.2、后驗概率

后驗概率是指事件發生后的條件概率。后驗概率是基于先驗概率求得的反向條件概率。概率形式與條件概率相同

例如，我們了解到判斷西瓜是否好瓜的一個指標是紋理。一般來說，紋理清晰的西瓜是好瓜的概率更大，假設是75%，如果把紋理清晰當作一種結果，然后去推測好瓜的概率，那么這個概率就被稱為后驗概率

1.2.3、條件概率

條件概率是指一個事件發生后另一個事件發生的概率。一般的形式為P(B|A)，表示事件A已經發生的條件下，事件B發生的概率
$$P(B|A)=\frac{P(AB)}{P(A)}$$

1.2.4、貝葉斯公式

貝葉斯公式是基于假設的先驗概率與給定假設下觀察到不同樣本數據的概率提供了一種計算后驗概率的方法。樸素貝葉斯模型依托于貝葉斯公式
$$P(A|B)=\frac{P(B|A)P(A)}{P(B)}$$

貝葉斯公式中：

• P(A)是事件A的先驗概率，一般都是人主觀給定的。貝葉斯中的先驗概率一般特指它
• P(B)是事件B的先驗概率，與類別標記無關，也稱標準化常量，通常使用全概率公式計算得到
• P(B|A)是條件概率，又稱似然概率，一般通過歷史數據統計得到
• P(A|B)是后驗概率，后驗概率是我們求解的目標

由于P(B)與類別標記無關，因此估計P(A|B)的問題最后就被我們轉化為基于訓練數據集樣本先驗概率P(A)和條件概率P(B|A)的估計問題

貝葉斯公式揭示了事件A在事件B發生條件下的概率與事件B在事件A發生條件下的概率的關系

更多關于條件概率、全概率公式與貝葉斯公式的介紹詳見文章：傳送門

1.3、貝葉斯定理的推導

根據條件概率公式可得
$$P(AB)=P(B|A)P(A)$$

同理可得
$$P(BA)=P(A|B)P(B)$$

設事件A與事件B互相獨立，即$P(AB)$=$P(BA)$，則有
$$P(B|A)P(A)=P(A|B)P(B)$$

由此可得貝葉斯公式
$$P(A|B)=\frac{P(B|A)P(A)}{P(B)}$$

1.4、樸素貝葉斯及原理

基于貝葉斯定理的貝葉斯模型是一類簡單常用的分類算法。在假設待分類項的各個屬性相互獨立的前提下，構造出來的分類算法就稱為樸素的，即樸素貝葉斯算法

所謂樸素，就是假定所有輸入事件之間相互獨立。進行這個假設是因為獨立事件間的概率計算更簡單，當然，也更符合我們的實際生產生活

樸素貝葉斯模型的基本思想是，對于給定的待分類項 X { x 1 , x 2 , . . . , x n } X\{{x_1,x_2,...,x_n}\} X{x1?,x2?,...,xn?}，求解在此項出現的條件下各個類別 P ( y i ∣ X ) P(y_i|X)