ref：
1.強推閉環增益、環路增益和PM關系說明 https://zhuanlan.zhihu.com/p/462528974
2.https://zhuanlan.zhihu.com/p/551710844>
3.何樂年 P130-負反饋閉環系統中的運算放大器環路增益的仿真測量
4.stb仿真環路增益 https://blog.csdn.net/jay183986697/article/details/104539035

一、引言

在設計運放時，相位裕度是一個重要的參數，因為運放通常工作在閉環中，相位裕度對閉環的穩定性和時域響應都有影響。而開環的運放就相當于一個性能一般的比較器。那如何對運放的相位裕度進行考慮、測量就很重要。

二、巴克豪森判據、最壞情況下的相位裕度、相位裕度

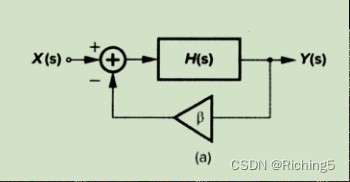
對于一個如下圖的負反饋系統，其系統閉環傳遞函數（閉環增益）為：

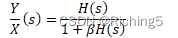
H(s)為運放開環增益。

若有w1使得βH(s=jw1)=-1則環路增益無窮大會產生振蕩。此條件可以表達為下式，這就是巴克豪森判據：

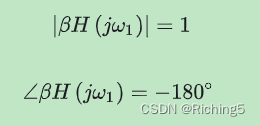
根據巴克豪森判據可以看出，判斷反饋系統是否穩定主要取決于環路響應βH(s)。但在設計運放中我們通常是將運放開環響應的GBW頻率處的剩余相位當作相位裕度，因為β=1時閉環增益βH(s)變等價于開環增益H(s)。這實際是種適用所有反饋系數β下的最差相位裕度。這樣設計對可能使用在各種情況下的通用運放來說沒問題的，但對于芯片內部一些β為確定值的情況，便會存在過設計，造成一些性能浪費。

PM有兩種計算方式，在part.三中會進行說明，但在具體仿真中我們發現用閉環測PM是更為合理的，這樣測不會忽略由于反饋網絡和寄生電容（例如mos輸入電容）形成的意料之外的極點。

注意巴克豪森判據可以看出，PM是找環路增益為1時，環路增益的相位曲線離-180°的距離，而非閉環響應的，避免混淆概念。

三、相位裕度與開環，環路，閉環增益的關系

圖中展示了次極點在GBW外的單極點系統的環路增益、閉環增益和相位的關系，注意由于β是實數，所以環路增益的相位本質上和開環增益的相位是同一條曲線，但閉環增益和開環增益的相位曲線并不一樣。 從紅到藍β逐漸增大。注意該曲線繪制在對數坐標系下。從圖中可以知道：
1.（a）中可以看出隨著β增加，環路增益幅度整體上移，環路增益的GBW增加。
2.（b）中灰色線為開環增益，通過閉環增益公式，可以知道開環增益和閉環增益的差值（dB）大概是環路增益，因此環路增益=0dB時即βAopen=1，則環路增益=0dB的頻率點為Aopen與Aclose重新交合的點（也是閉環主極點位置），前提是單極點系統。閉環后系統由于極點頻率從w0變為(1+βAopen)w0，所以帶寬增加，但閉環增益GBW并沒有變化。
3.計算PM可以找βAopen=0dB或Aopen與Aclose的交點對應頻率點下的開環增益的相位曲線。
4.（c）由于是單極點系統，隨著β增加，環路增益幅度整體上移，GX點后移，高頻極點開始起作用，所以對應PM下降。
5.由于β3=1，所以圖(a)中β3Aopen的曲線就是運放的開環增益曲線。我們在設計運放時，常常通過檢查GBW處剩余的相位作為運放的相位裕度，實際上得到的就是該運放在β3=1這個相位裕度最壞情況下的值。單位增益負反饋下的相位裕度等于開環仿真的相位裕度。
6.測PM的方法：找閉環增益和開環增益交點頻率下的開環相位曲線來計算；找環路增益=0dB的頻率下的環路增益相位曲線來曲線。在part.4.2中會說明后者是更優的測量方法，因為前者會忽略寄生電容和反饋網絡形成的極點。

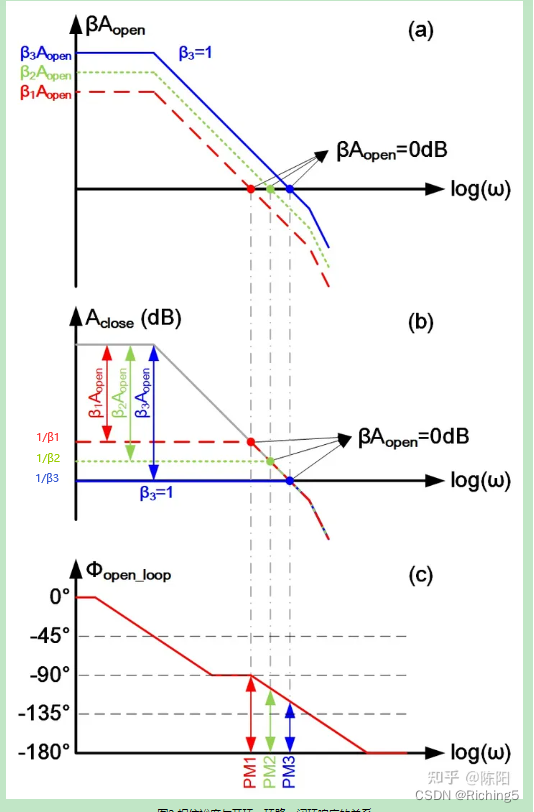
綜上，反饋系數越大，PM越小，環路增益越高，環路增益的GBW越高，閉環增益越低，閉環增益的GBW不變。

四、環路增益、閉環增益和相位的仿真

這個部分嘗試分別用雙入單出和全差分運放構成的反饋系統來仿真環路增益、閉環增益和PM。

4.1 運放為雙入單出時

使用的運放為一個理想元件構成的二級密勒補償運放，零和次極點相抵消，GBW內只有一個極點，其性能指標為：

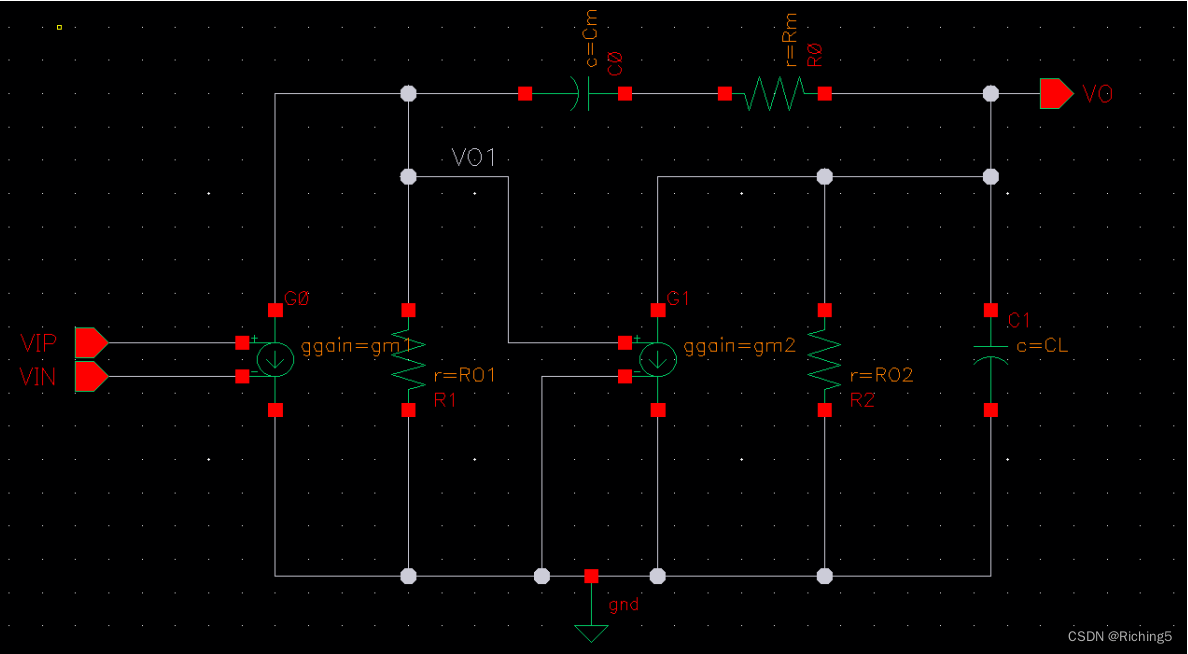
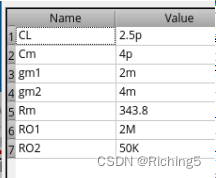
用上述電路構成一個反相比例放大電路：

Vo=-R2/R1*Vi

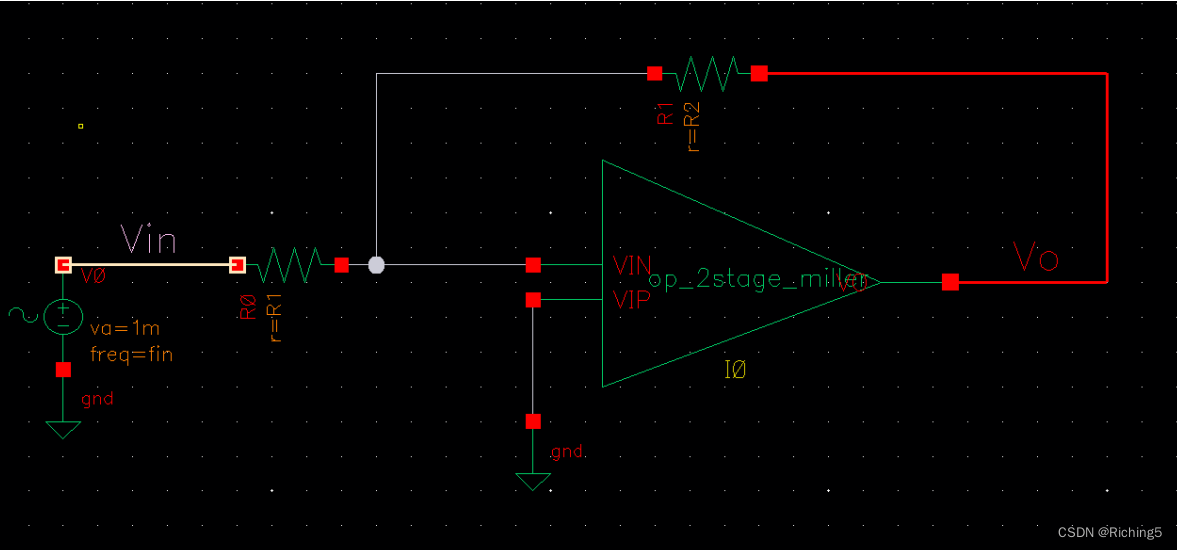
設置R2=900k，R1=100k，輸入頻率為1kHz，幅度為1mV的信號時，輸出幅度為9mV，頻率為1kHz，因為反饋拓寬了帶寬（閉環帶寬遠大于運放帶寬），所以并不會衰減信號。

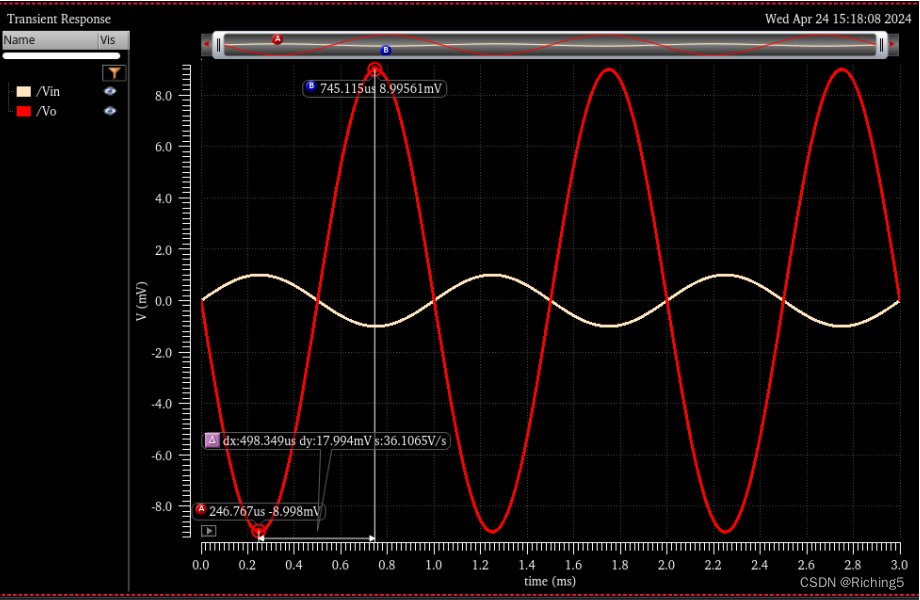
4.1.1 系統的閉環增益

仿真閉環增益的電路如下，對其進行閉環仿真。

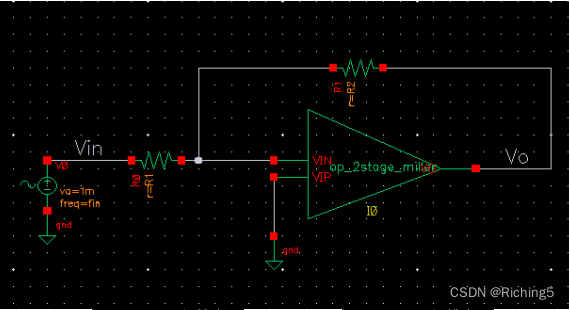
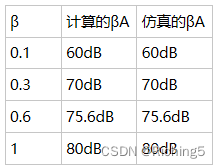
分別設置β=0.1/0.3/0.6=R1/(R1+R2)，則閉環增益分別為10（20dB）、3.3（10.4dB）、1.6（4dB）得到以下閉環增益曲線：

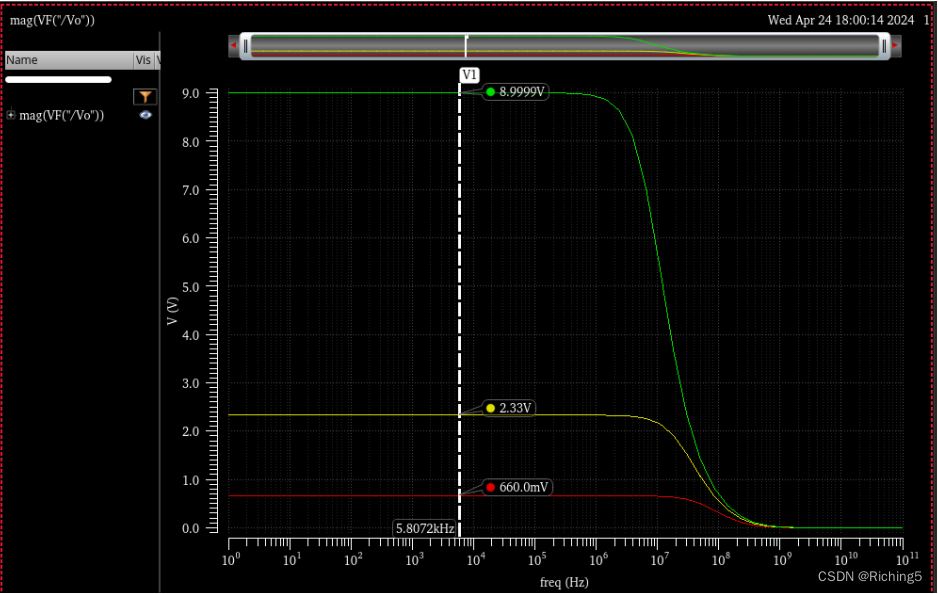
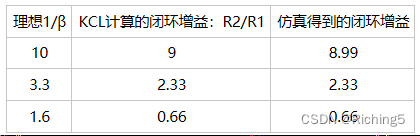
可以看到閉環增益并不嚴格等于1/β=1+R2/R1，這主要是沒有去考慮加載效應對開環增益和反饋系數的影響，而如果采用KCL計算出來的閉環增益是R2/R1，這是更接近仿真中的閉環增益：

將運放開環增益（粉色）和不同β的閉環增益繪制幅頻特性曲線在對數坐標系下，和第三節圖對應：隨著R2的增加，β降低，閉環增益的帶寬降低，GBW變化并不顯著。

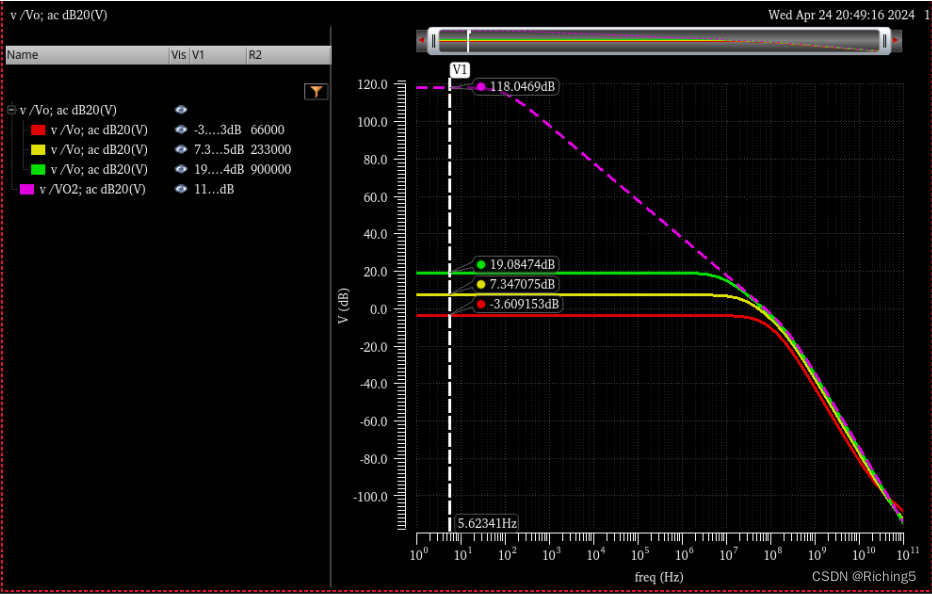
4.1.2 stb仿真系統的環路增益和相位裕度（環路穩定性）

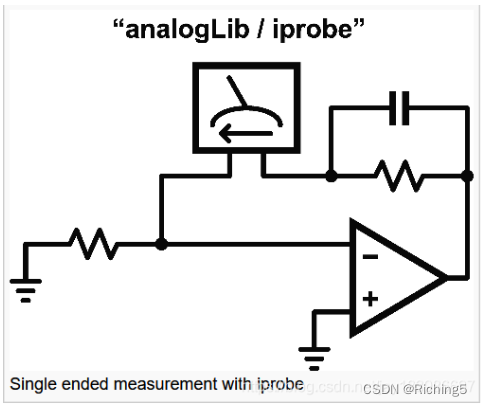
將iprobe放在環路中，極性不重要，輸入交流接地，設置stb仿真：

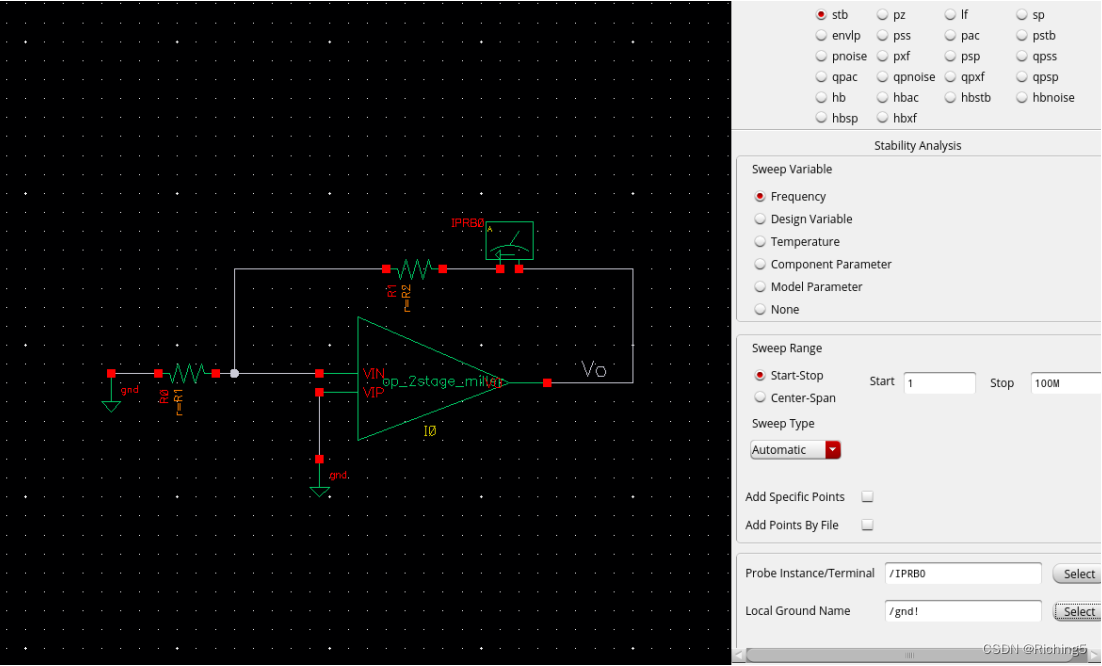
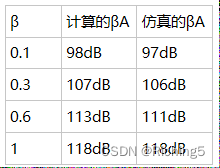
分別設置β=0.1/0.3/0.6/1，得到以下環路增益的幅頻曲線：可見仿真的環路增益和理論計算值還是很接近的。注意這里的Phase Margin就是實際的PM，不用再加180°。

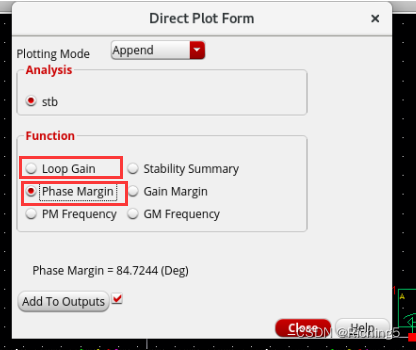
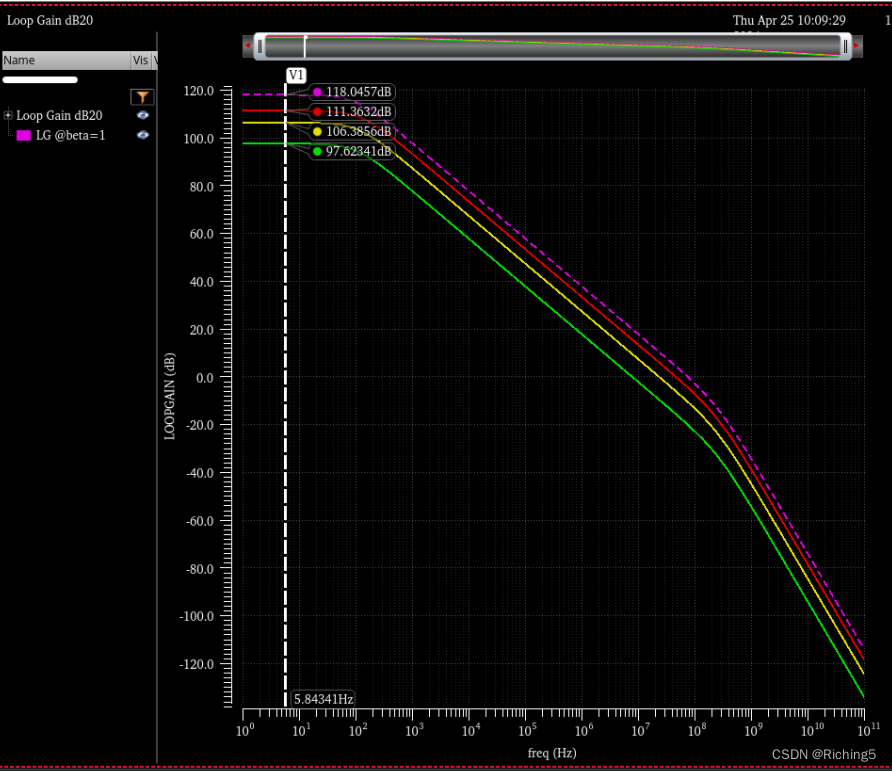
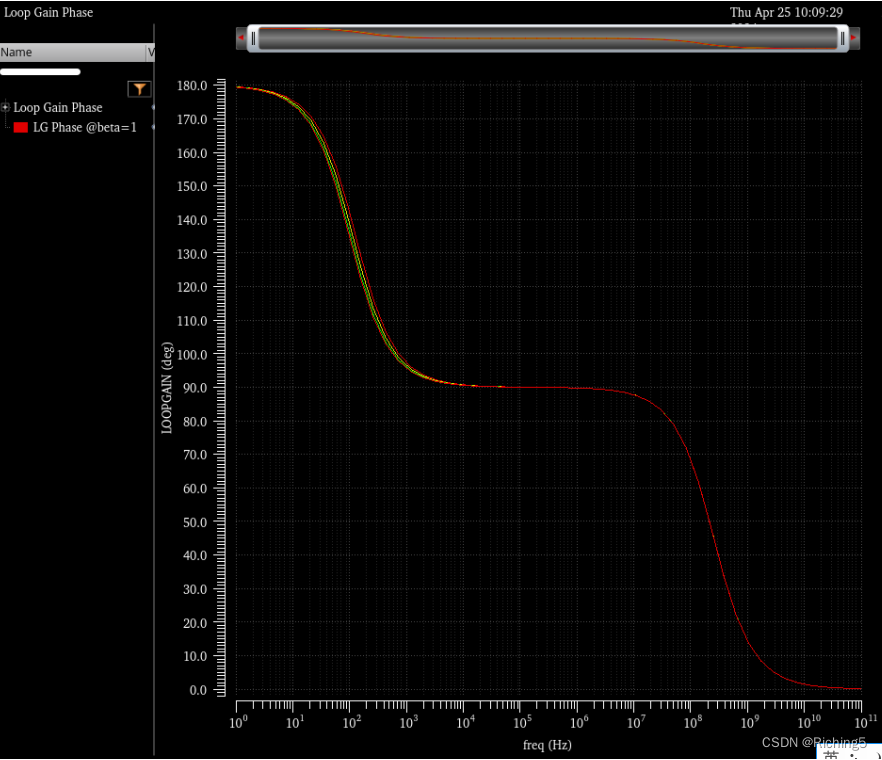
β對相位曲線并沒有顯著影響，因為這里的β是實數：

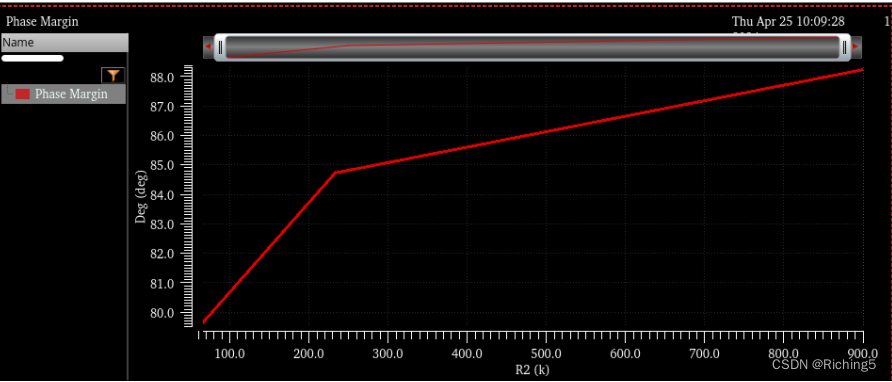
環路增益的PM隨著β的降低而增加：

除了用stb確定環路增益的PM，還可以開環仿真找到Gain為1/β處的相位裕度就是實際的相位裕度。因為開環相位裕度和閉環增益的相位裕度是一樣的，因為β是一個實數，從開環傳遞函數H(s)到環路增益βH(s)并不會改變相位頻率曲線。

4.2 運放為全差分時

使用的全差分運放為建模的全差分運放，其性能指標如下：

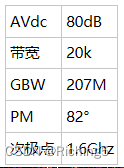
4.2.1 系統的閉環增益

仿真閉環增益電路圖如下：注意反饋電阻兩端的連接。

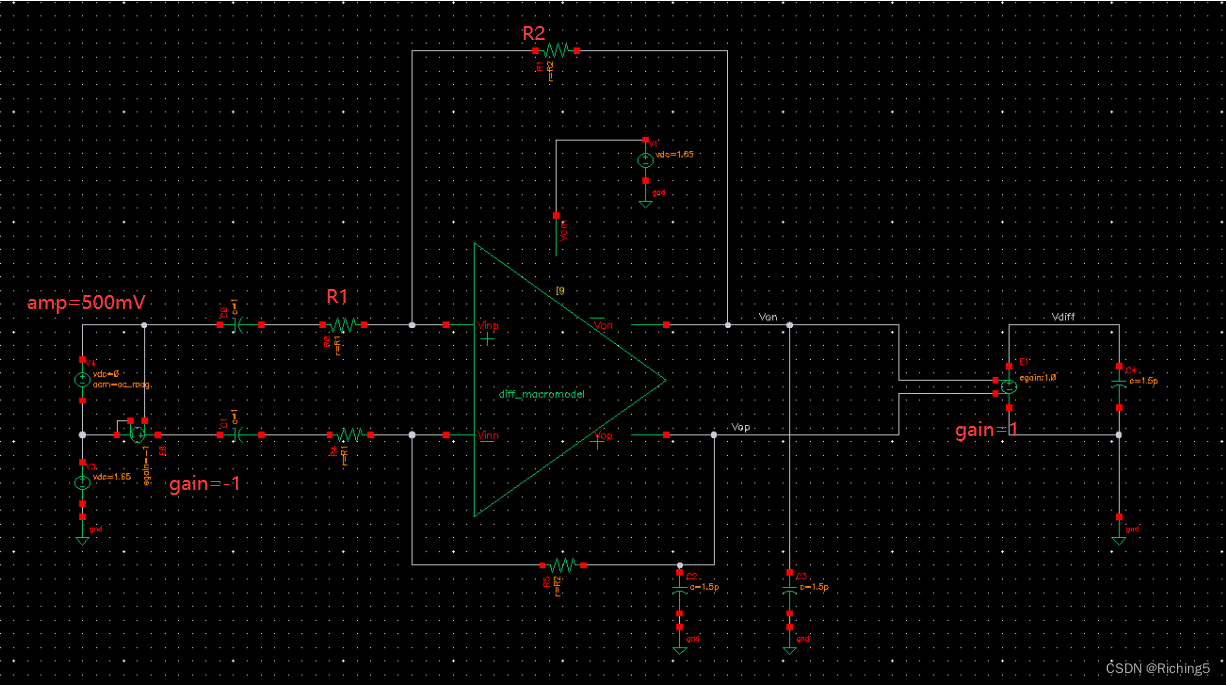
分別設置β=0.1/0.3/0.6=R1/(R1+R2)，將閉環增益和開環增益畫在一起：結果和4.1.1類似，但在閉環增益的主極點處有尖峰且隨β增加而顯著。從SansenP110中可以知道尖峰是由于PM不足導致的，但從開環增益的相位來看明明PM是充足的，存在矛盾。

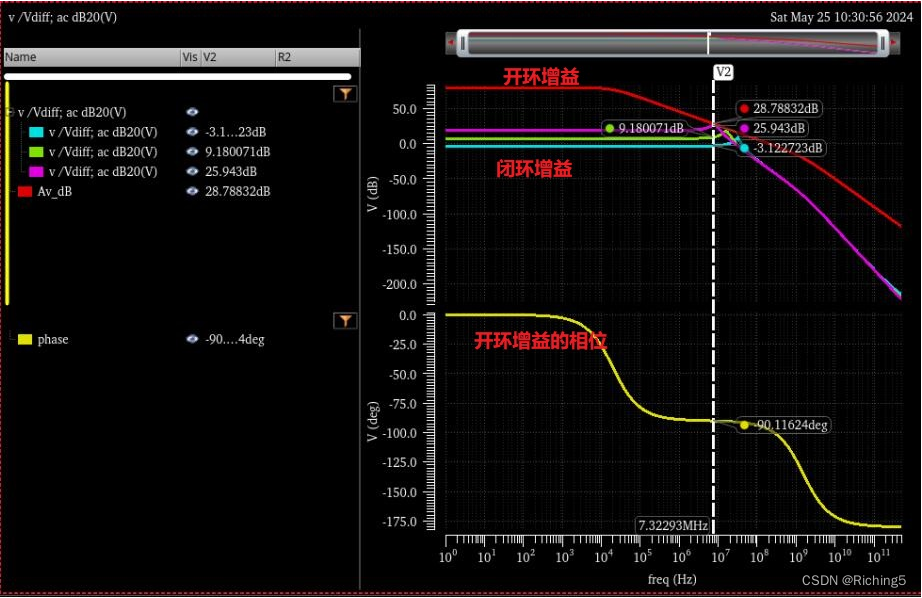
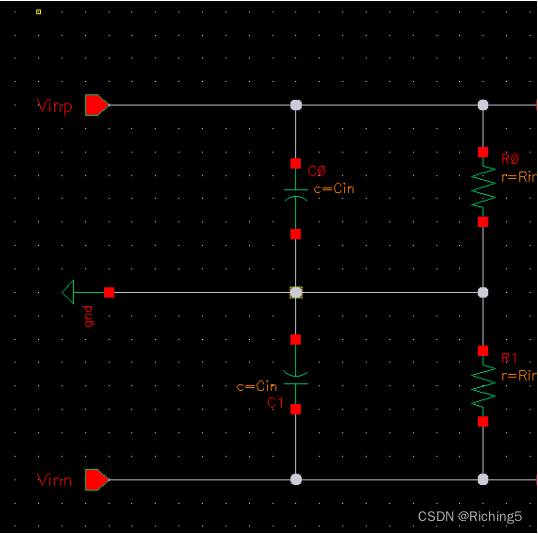
先給結論，這是因為所使用的理想運放建模的輸入電容Cin=500f較大，輸入電容和反饋電阻形成了額外的極點，但這個極點在開環增益、相位和閉環增益中并看不到。這就是這種方法的局限性。接下來用stb測LG的方式進行驗證。

https://bbs.eetop.cn/thread-970084-1-1.html

4.2.2 stb仿真系統的環路增益和相位裕度（環路穩定性）

這里使用diffstbprobe接入環路進行仿真。

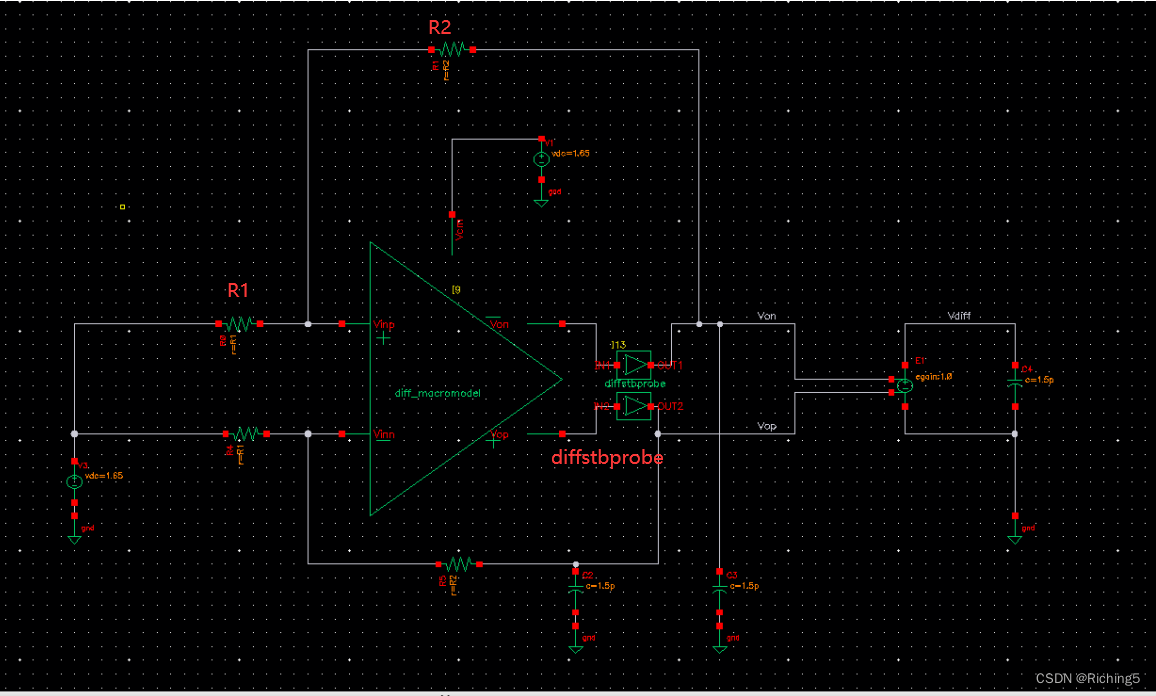
也可以使用cmdmprobe，但要設置CMDM=-1

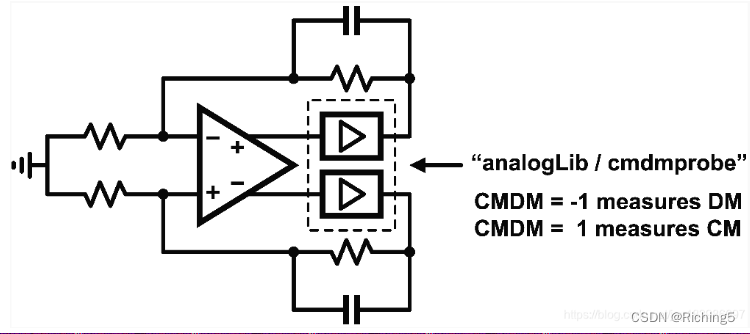
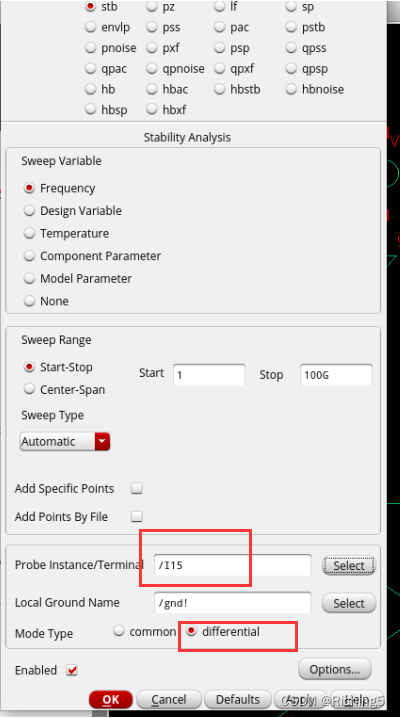
設置stb仿真，選擇圖中的diffstbprobe

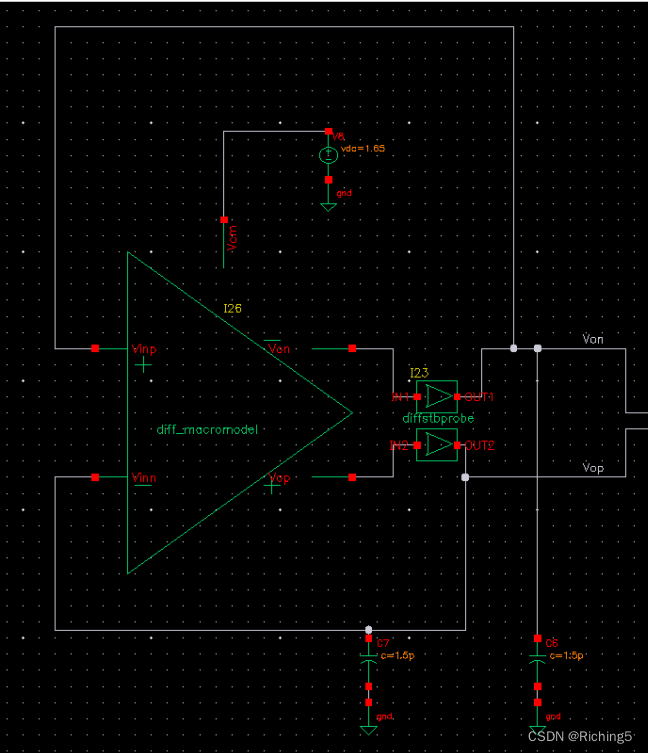
仿真單位增益的電路如下：不需要輸入提供DC，而是通過單位反饋運放自己確立DC。

不同反饋系數下的LG的頻率特性曲線和預期基本一致。

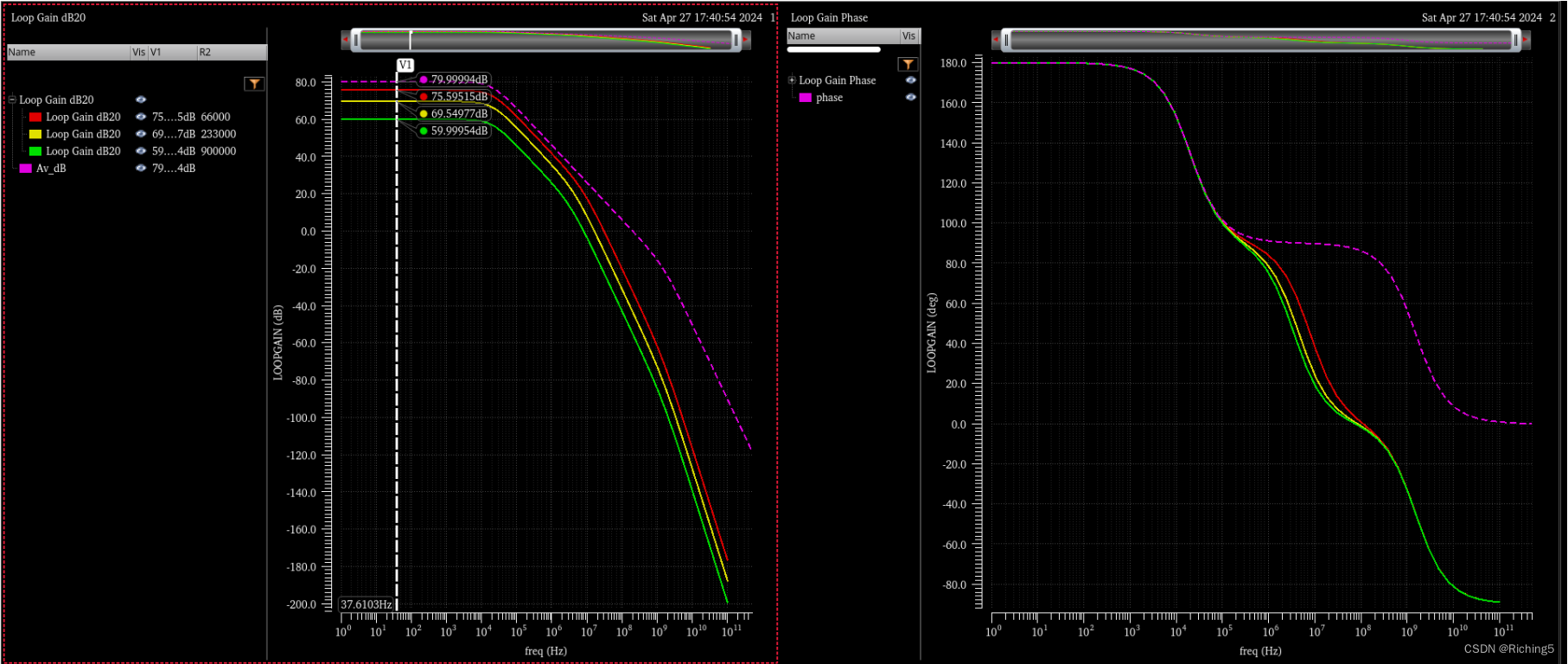
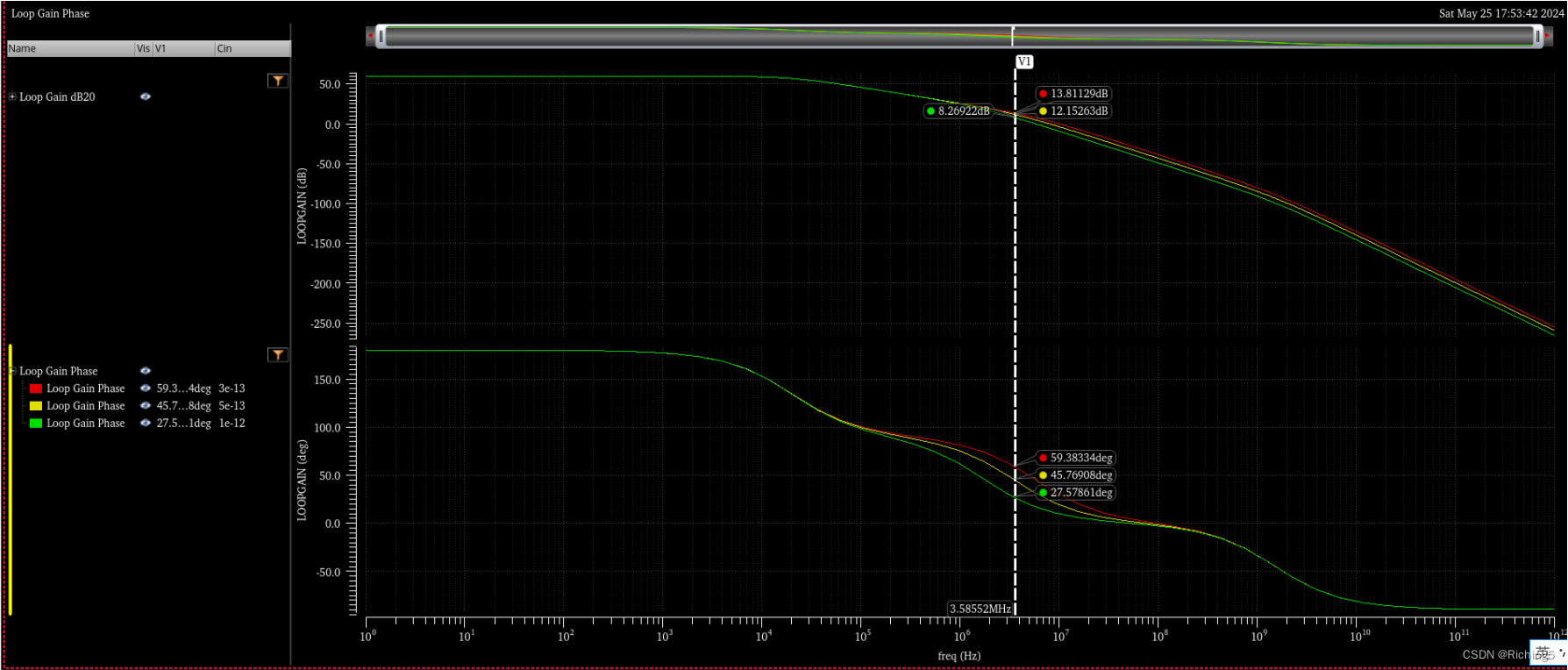
但可以看到電阻反饋時LG的極點數目相比于單位負反饋時多了一個，位于開環增益的主次極點之間，通過調整輸入電容Cin可以看到LG中間的極點位置會變化，這驗證了前面的結論，且Cin=500f，R1=100k，R2=900k，可以計算出f=1/(2piR1R2/(R1+R2)*Cin)=3.5Mhz和圖中對應。

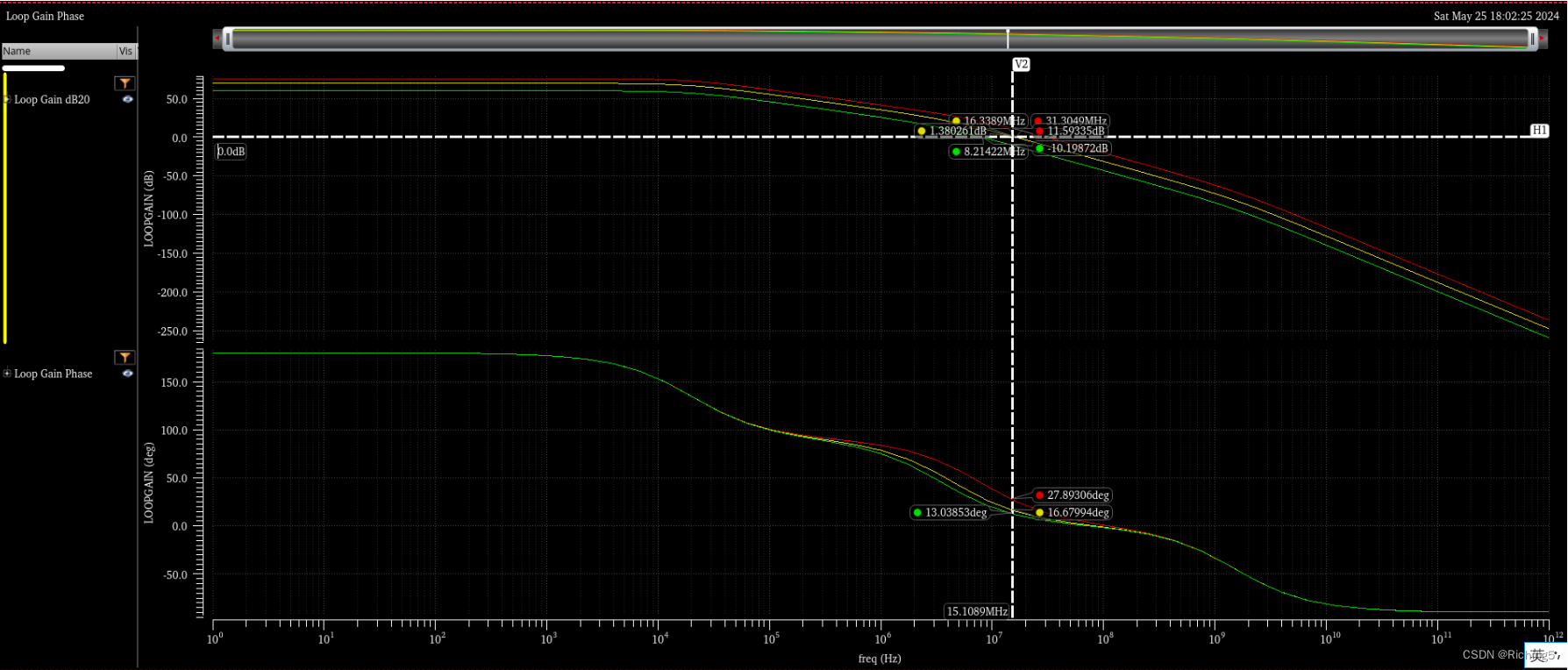
畫出β=0.1/0.3/0.6時的LG

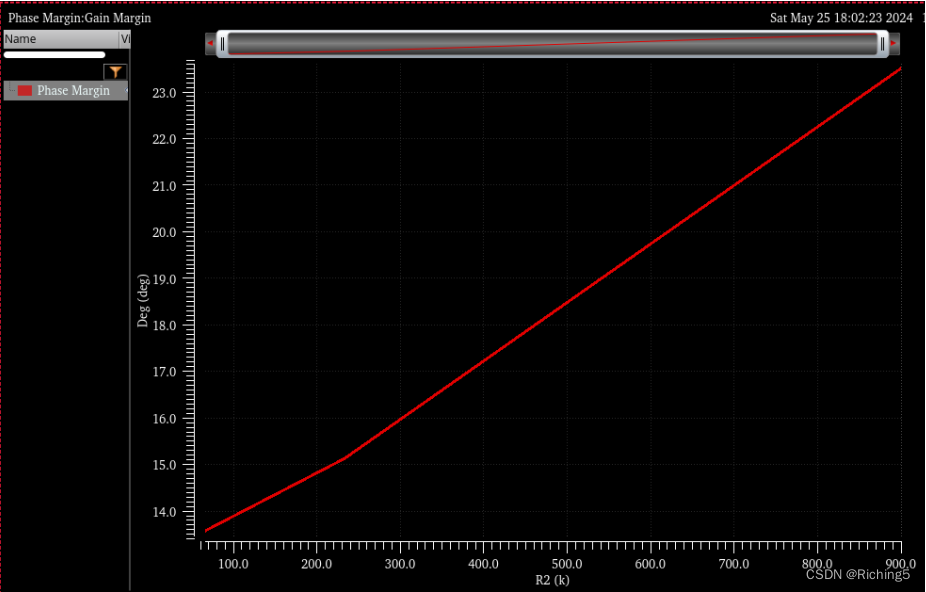
可以看到實際上PM是很小的，這也是前面閉環增益的尖峰的原因。

五、總結

不論全差分還是雙入單出，穩定性判斷、PM計算就在閉環時用stb仿真，根據Loop gain=0dB時的Loop gain phase計算PM。對于通用運放，就在單位反饋下用stb仿真PM和穩定性；對于特定應用場景，將運放接成特定負反饋系統再進行stb仿真PM和穩定性。