本次實現的二叉搜索樹并不是AVL數和紅黑樹，只是了解流程和細節。

二叉搜索樹的概念

二叉搜索樹并不是單純存儲數據。所以他有規則：
①.左子樹比根小，右子樹比根大。

②.搜索二叉樹不建議用遞歸。

二叉搜索樹一定要遵循這個規律！否則他都不能算是二叉搜索樹！

K模型二叉搜索樹的實現

二叉搜索樹的架構

我們之前也學過二叉樹，二叉樹的結構是節點里面放了左右指針和值，所以節點就是一下結構。 而二叉樹的本身就是又一個根節點連接起來的。

template<class T>
struct BinarySearchTreeNode
{BinarySearchTreeNode(T& key):_key(key), _left(nullptr), _right(nullptr){}T _key;BinarySearchTreeNode* _left;BinarySearchTreeNode* _right;
};template<class T>class BinarySearchTree{public:typedef BinarySearchTreeNode<T> Node;		private:Node* _root=nullptr;};

insert插入

插入一定要遵循規則：
①.左子樹比根小，右子樹比根大。 不是這個規則都不是二叉搜索樹。

(1). 當你插入第一個值的時候，他就是根，所以我們要特殊處理，當_root==nullptr時，要把第一個插入的值變成根。
(2).除第一個值之后的值就要遵行規則。

bool insert(T& x)
{if (_root == nullptr){Node* noeNode = new Node(x);_root = noeNode;return true;}Node* cur = _root;Node* parent = cur;while (cur){if (cur->_key < x){//大于在右邊parent = cur;cur = cur->_right;}else if (cur->_key > x){//小于在左邊parent = cur;cur = cur->_left;}else{//等于,二叉搜索樹不允許冗余，所以直接返回false。return false;}}Node* newNode = new Node(x);if (newNode->_key > parent->_key)parent->_right = newNode;elseparent->_left = newNode;return true;
}

find 查找

查找就很簡單，只要把前面的代碼復制一半，當查找到了，我們就返回true，到空了都沒找到就返回false。

bool find(const T& x)
{Node* cur = _root;Node* parent = cur;while (cur){if (cur->_key < x){//大于在右邊parent = cur;cur = cur->_right;}else if (cur->_key > x){//小于在左邊parent = cur;cur = cur->_left;}else{//等于，找到了return true;}}return false;
}

中序遍歷Inorder

中序遍歷我們都很了解了，但是問題是，我們要把根傳入，根一定是私有的，你在類外訪問不了。這個時候我們就可以套一層。

public：
void Inorder()
{_Inorder(_root);cout << endl;
}
private:void _Inorder(Node* _root){if (_root == nullptr) return;_Inorder(_root->_left);cout << _root->_key<< " ";_Inorder(_root->_right);}Node* _root=nullptr;

刪除earse

刪除其實很麻煩，有很多種情況。因為二叉搜索數一定是滿足規則的，所以我們刪除不能混亂了規則，而是繼續保持規則。所以我們要用替換法，保證規則不亂。

替換法的思路

因為我們要保證規則不亂，那么我們可以用替換法，讓左樹的最大值/右樹的最小值與當前值替換，因為當前節點的左邊一定比他小，右邊一定比他大，那么當我們用左邊最大值，替換了當前節點，也不會改變規則；右邊同理。

情況一 ：假如要刪除節點左邊是空的。

在左邊時

假如我要刪除9這個節點。并且左側是空，那么我們是不是可以直接讓他父親的左邊指向他的右邊？思考一下！

為什么？左側為空，當前刪除節點的左側一定是什么都沒有的，右邊可有可無，但是右邊沒有也沒關系，一樣置空，有的話，我們就需要讓他的父親鏈接他的孩子。

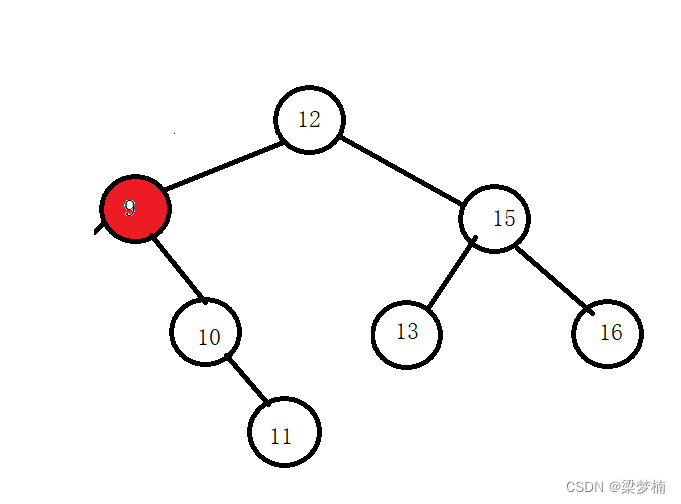
并且我們發現并不用替換法，就可以直接鏈接后刪除。

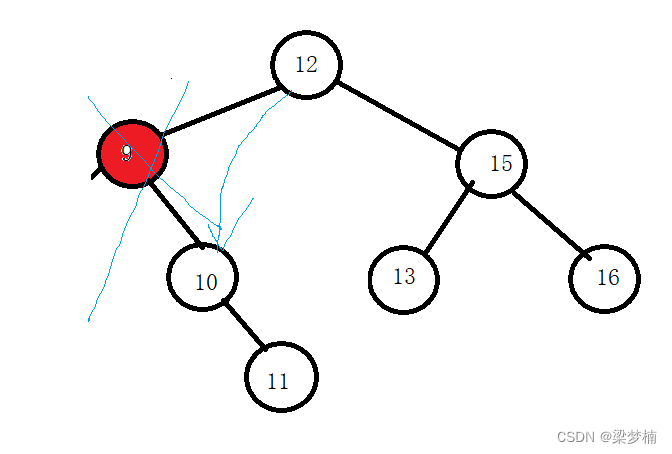
在右邊時

其實在右邊也是一樣的，只不是我們要特殊判斷一下，刪除節點時父親的左邊還是右邊，方便我們鏈接。

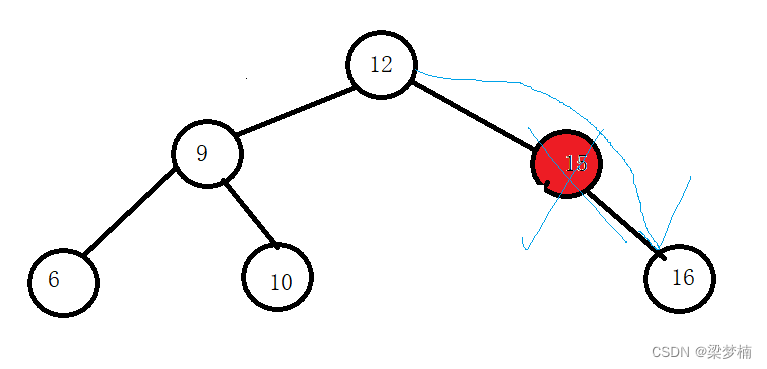
情況二：假如要刪除節點右邊是空的。

是父親的右邊時

那么他右邊一定是沒有值的，左邊的值可有可無，那么我們就需要讓它的父親指向他的左值就可以了。

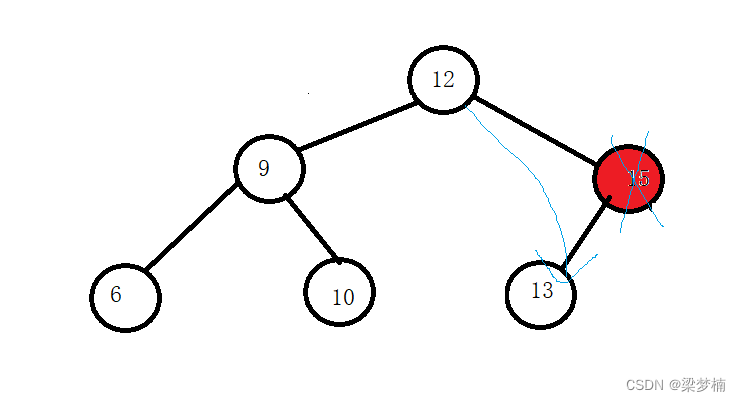
是父親的左邊時

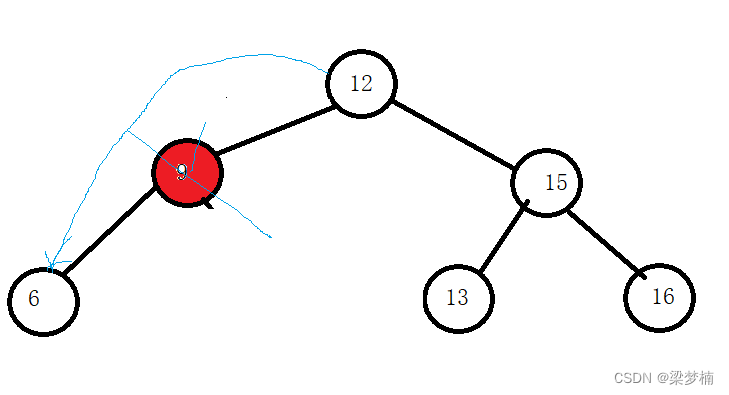
情況三：兩邊都有值

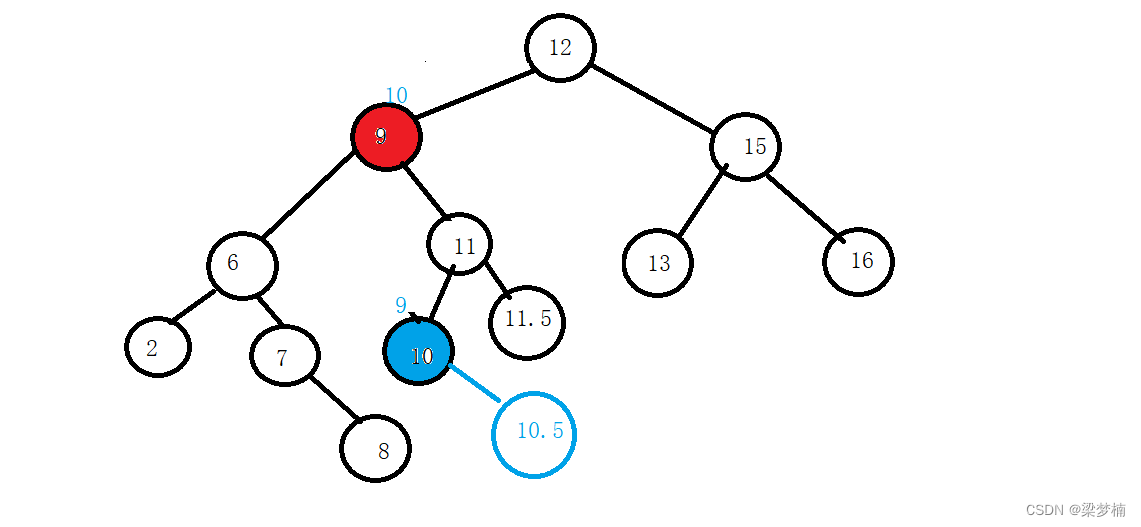
如果這棵樹是這樣的，那么我要刪除9怎么做呢？就需要替換法，我們需要找左邊最大值或者右邊最小值，我們假設要找是右邊最小值。

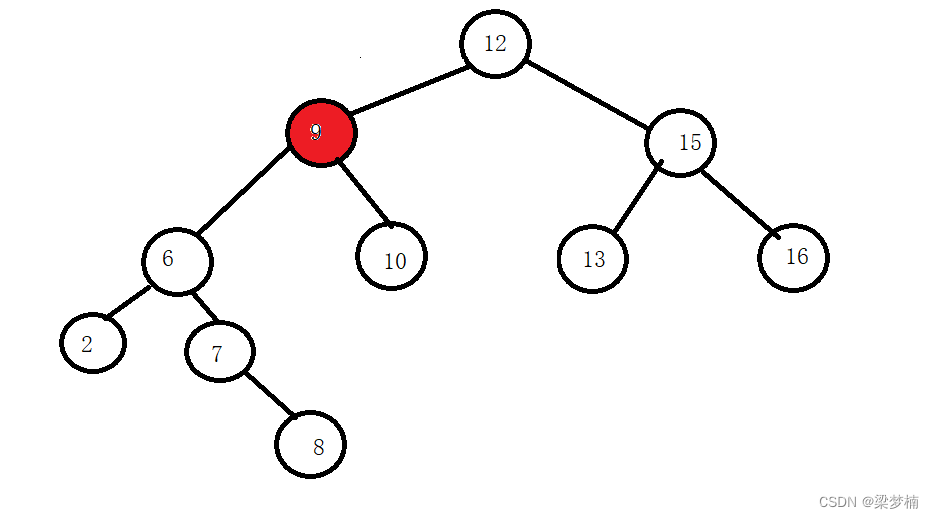
從當前節點開始找，右邊最小值是10(藍色標記)。

問：為什么要從當前節點找，而不是從根開始？
答：如果從根開始找，你會發現，當我們交換后，不滿足條件了。圖中右邊最小值是13，如果換到最左邊那就不滿足二叉搜索的要求了，所以要從當前節點找，因為當前節點的右邊跟當前這個位置換一定是比大，比其他節點小的。

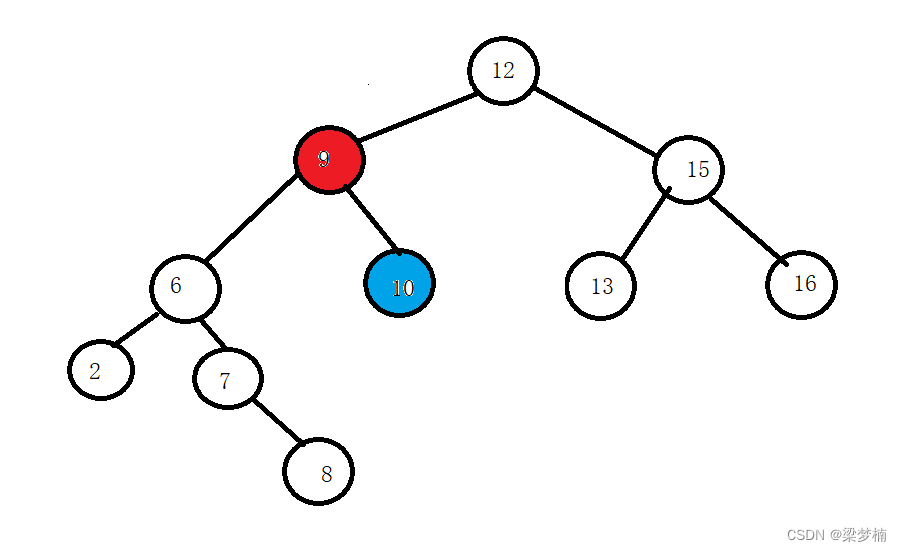
當我們都找到了，我們就要用交換法。將兩個值交換后，左邊最小的那個節點就是我們要刪除的。那么我們就需要把最小節點的右邊給它的右邊。

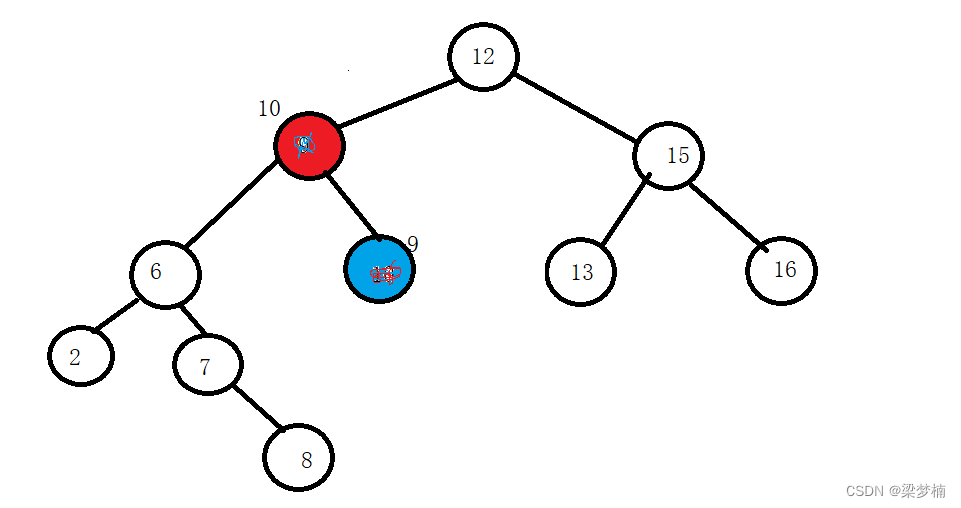
左邊

這里給大家道個歉，因為數字太過緊湊，所以湊不出數，只能讓整型和浮點數混合了，在實際場景中是不可能有的，只是舉個例子。

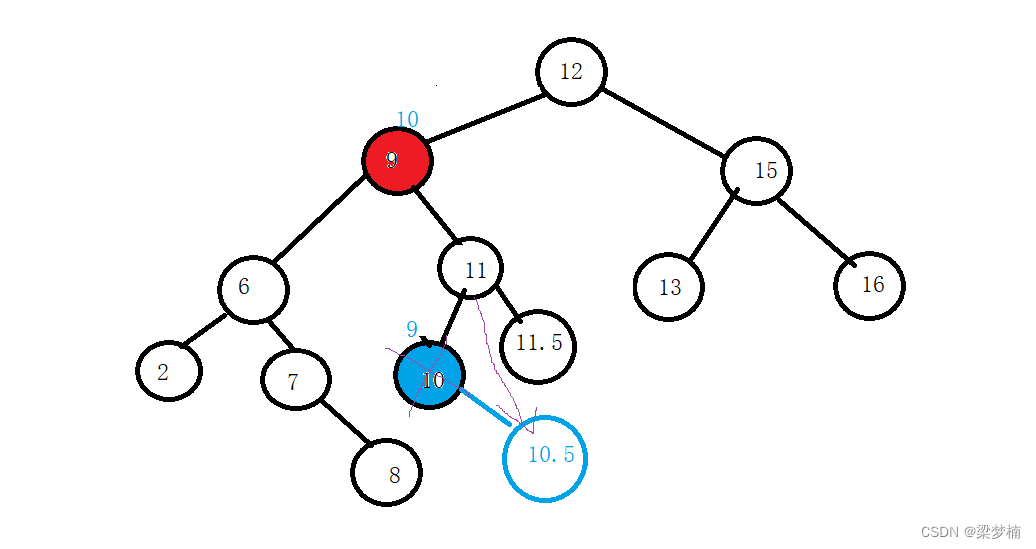
假設我們交換后，發現要刪除的節點右邊還有值，

問題：我怎么讓被刪除節點的父親知道是左邊還是右邊的節點間接我的右節點呢？
答：需要判斷一下，如果被刪除的節點是父親的左邊，就需要讓左邊指向被刪的右邊，如果是父親的右邊就讓父親的右邊指向被刪的右邊。

右邊

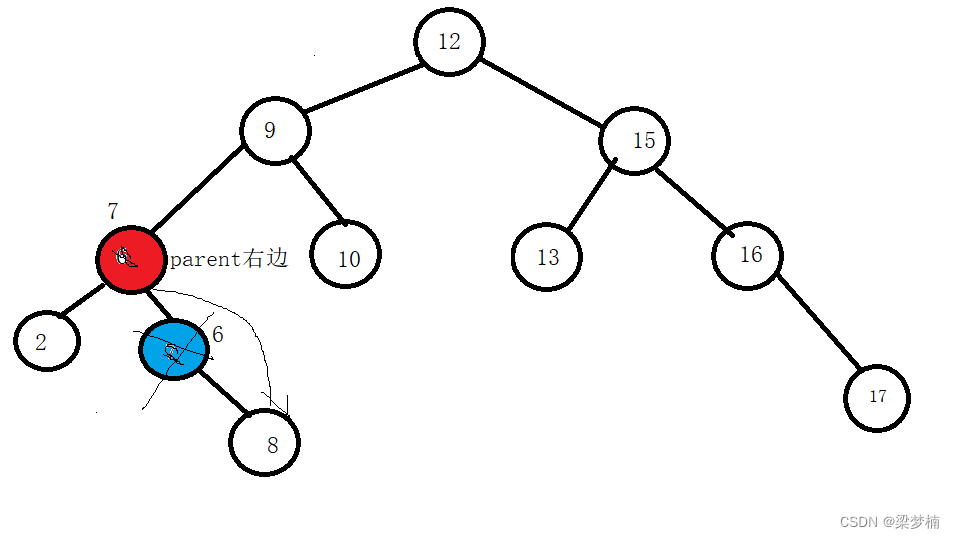
這種情況，就是他在父親的右邊，所以我們需要讓父親的右邊鏈接被刪的右邊。

代碼實現

雖然刪除的代碼很復雜，但是要注意的細節很多。
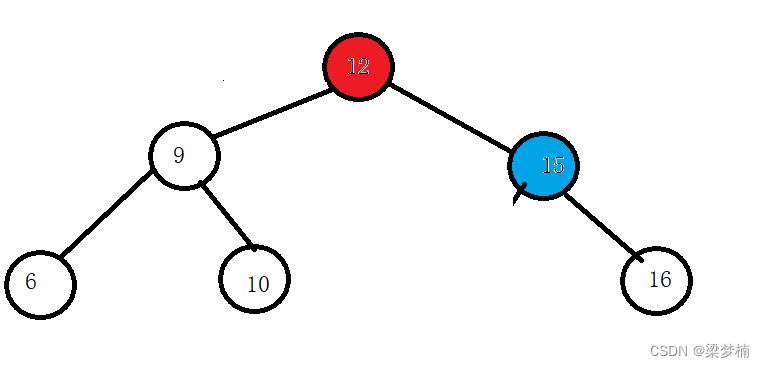
(1).在我們找到了當前被刪節點，情況三的時候，能不能讓Node* rightMinParent = nullptr;? 答：不可以，因為當我們刪除這種情況的時候，就會導致空指針訪問，因為循環我們沒有進去，但是鏈接值的時候，就會導致空指針訪問。

(2).在我們交換后，能不能遞歸把他刪了？不能！我問你交換后還滿足二叉搜索數的要求嗎？不滿足，你永遠都不會找到！

		bool erase(const T& x){Node* cur = _root;Node* parent = cur;while (cur){if (cur->_key < x){//大于在右邊parent = cur;cur = cur->_right;}else if (cur->_key > x){//小于在左邊parent = cur;cur = cur->_left;}else{//等于，找到了if (cur->_left == nullptr){//沒有值直接刪，把右邊給父親if (cur == parent->_left){parent->_left = cur->_right;delete cur;}else if(cur == parent->_right){parent->_right = cur->_right;delete cur;}}else if (cur->_right == nullptr){if (cur == parent->_left){parent->_left = cur->_left;delete cur;}else if (cur == parent->_right){parent->_right = cur->_left;delete cur;}}else{Node* rightMin = cur->_right;Node* rightMinParent = cur;//這里要讓父親是cur，刪根的時候就會出問題while (rightMin->_left){rightMinParent = rightMin;rightMin = rightMin->_left;}std::swap(cur->_key, rightMin->_key);if (rightMinParent->_left == rightMin)rightMinParent->_left = rightMin->_right;elserightMinParent->_right = rightMin->_right;delete rightMin;}return true;}}return false;}