系列文章目錄及鏈接

上篇：機器學習（五） -- 監督學習（2） -- 樸素貝葉斯
下篇：機器學習（五） -- 監督學習（4） -- 集成學習方法-隨機森林

---

前言

tips：標題前有“***”的內容為補充內容，是給好奇心重的寶寶看的，可自行跳過。文章內容被“文章內容”刪除線標記的，也可以自行跳過。“！！！”一般需要特別注意或者容易出錯的地方。

本系列文章是作者邊學習邊總結的，內容有不對的地方還請多多指正，同時本系列文章會不斷完善，每篇文章不定時會有修改。

由于作者時間不算富裕，有些內容的《算法實現》部分暫未完善，以后有時間再來補充。見諒！

文中為方便理解，會將接口在用到的時候才導入，實際中應在文件開始統一導入。

---

一、決策樹通俗理解及定義

1、什么叫決策樹（What）

????????決策樹（decision tree）是一種樹形結構，其中每個內部節點表示一個屬性上的判斷，每個分支代表一個判斷結果的輸出，最后每個葉節點代表一種分類結果。決策樹本質是一顆由多個判斷節點組成的樹。

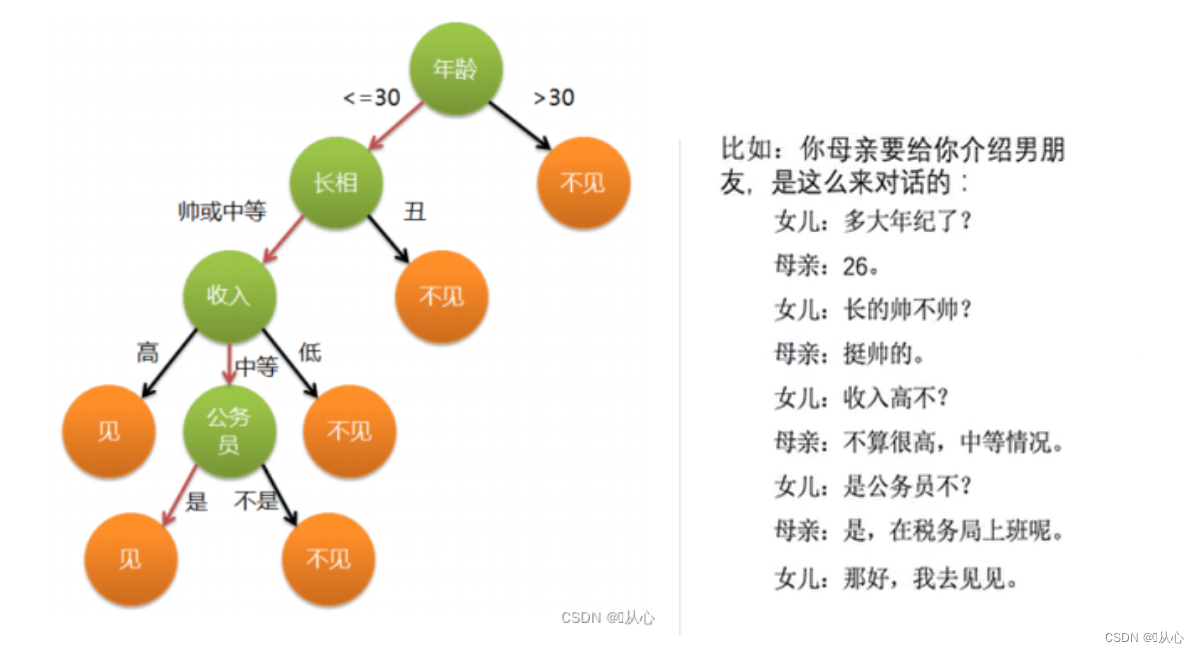
????????決策樹思想的來源非常樸素，程序設計中的條件分支結構就是if-else結構，最早的決策樹就是利用這類結構分割數據的一種分類學習方法。

????????決策樹的決策過程就是從根節點開始，測試待分類項中對應的特征屬性，并按照其值選擇輸出分支，直到葉子節點，將葉子節點的存放的類別作為決策結果。

2、決策樹的目的（Why）

決策樹學習的目的是為了產生一棵泛化能力強（即處理未見示例能力強）的決策樹。

3、怎么做（How）

決策樹通常有三個步驟：特征選擇、決策樹的生成、決策樹的修剪。

特征選擇：從訓練數據的特征中選擇一個特征作為當前節點的分裂標準（特征選擇的標準不同產生了不同的特征決策樹算法）。
決策樹生成：根據所選特征評估標準，從上至下遞歸地生成子節點，直到數據集不可分則停止決策樹停止聲場。
決策樹剪枝：決策樹容易過擬合，需要剪枝來縮小樹的結構和規模（包括預剪枝和后剪枝）。

決策樹：決策和樹兩步，構建樹形結構在前，決策在后。決策樹的生成過程中分割方法，即 屬性選擇的度量 是關鍵?

幾個問題：如何進行特征選擇？

按照某個特征對數據進行劃分時，它能最大程度地將原本混亂的結果盡可能劃分為幾個有序的大類，則就應該先以這個特征為決策樹中的根結點。

二、原理理解及公式

1、決策樹原理

1.1、決策樹組成

????????決策樹由結點和有向邊組成。結點有兩種類型：內部結點和葉節點。
????????????????內部結點表示一個特征或屬性，
????????????????葉節點表示一個類別，
????????????????有向邊則對應其所屬內部結點的可選項（屬性的取值范圍）。

????????在用決策樹進行分類時，首先從根結點出發，對實例在該結點的對應屬性進行測試，接著會根據測試結果，將實例分配到其子結點；然后，在子結點繼續執行這一流程，如此遞歸地對實例進行測試并分配，直至到達葉結點；最終，該實例將被分類到葉結點所指示的結果中。?

1.2、決策樹的構建

決策樹的本質是從訓練集中歸納出一套分類規則，使其盡量符合以下要求：

1. 具有較好的泛化能力；
2. 在 1 的基礎上盡量不出現過擬合現象。

當目標數據的特征較多時，應該將樣本數據的特征按照怎樣的順序添加到一顆決策樹的各級結點中？這便是構建決策樹所需要關注的問題核心。
也就是前面說的如何特征選擇。按照某個特征對數據進行劃分時，它能最大程度地將原本混亂的結果盡可能劃分為幾個有序的大類，則就應該先以這個特征為決策樹中的根結點。

基于此，引入信息論中的“熵”。

2、信息論基礎

2.1、熵

2.1.1、概念

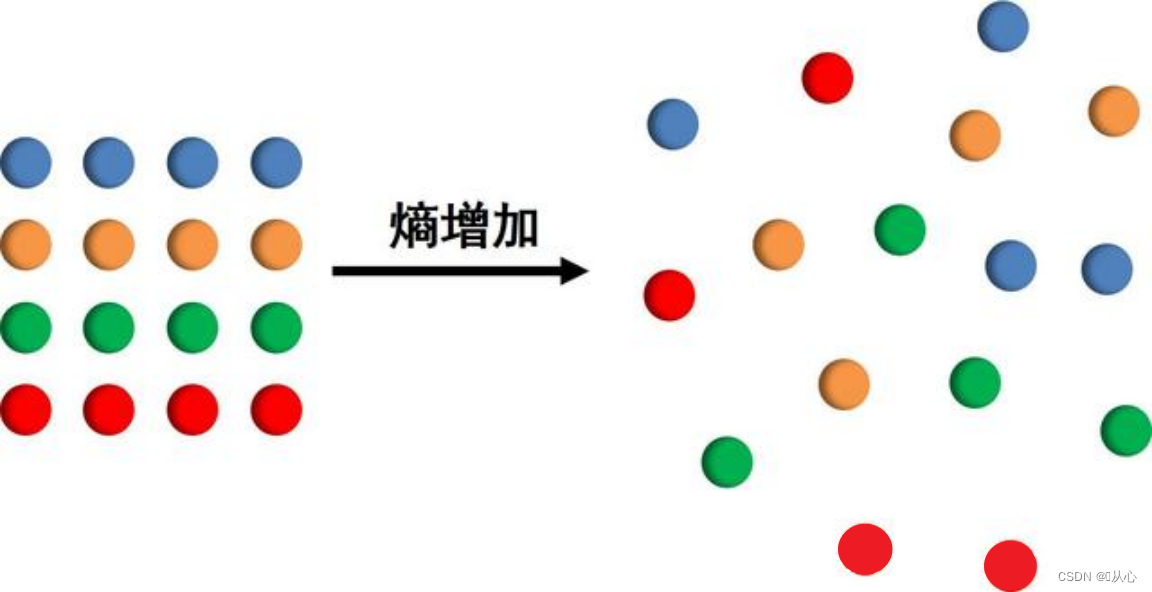
熵（Entropy)是表示隨機變量不確定性的度量，即物體內部的混亂程度。
比如下圖中，從 左到右表示了熵增的過程。
系統越有序，熵值越低；系統越混亂或者分散，熵值越高。
對于決策樹希望分類后的結果能使得整個樣本集在各自的類別中盡可能有序，即最大程度地降低樣本數據的熵。

2.1.2、熵的公式

D為訓練數據集所有樣本，K為所劃分的類別數量，pk是k類樣本的概率密度：（H(X)是另一種表達形式。）

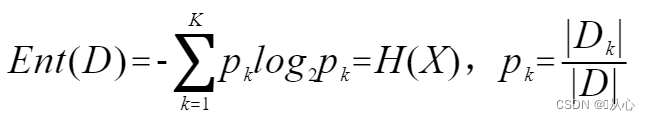
當pk=0或pk=1時，H(X)=0,隨機變量完全沒有不確定性
當pk=0.5時，H(X)=1,此時隨機變量的不確定性最大

eg：顯然A集合的熵值要低，A中只有兩種類別，而B中類別太多了，熵值就會大很多。

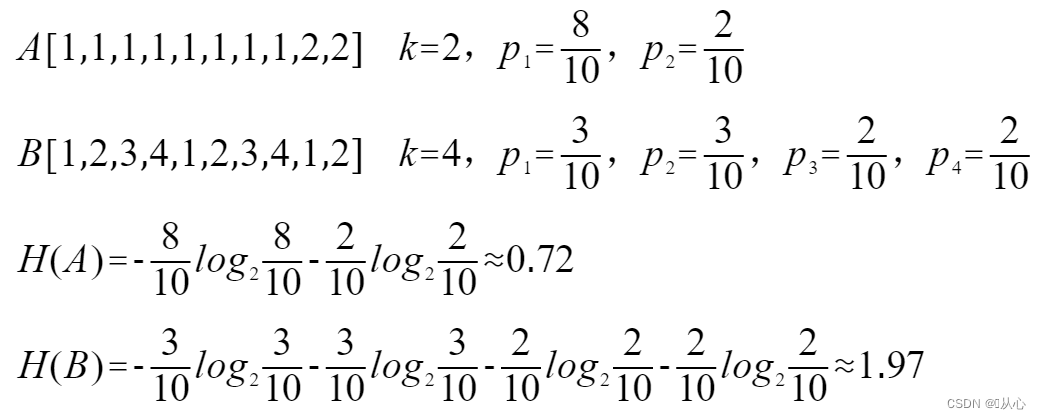
常用的最優屬性選取方法有三種：

• 信息增益：在 ID3 決策樹中使用
• 信息增益率：在 C4.5 決策樹中使用
• 基尼系數：在 CART 決策樹中使用

2.2、信息增益（決策樹的劃分依據一）--? ID3

2.2.1、概念

以某特征劃分數據集前后的熵的差值。

熵可以表示樣本集合的不確定性，熵越大，樣本的不確定性就越大。因此可以使用劃分前后集合熵的差值來衡量使用當前特征對于樣本集合D劃分效果的好壞。

信息增益 = ent(前) - ent(后)

2.2.2、公式

特征A對訓練數據集D的信息增益g(D,A),定義為集合D的信息熵H(D)與特征A給定條件下D的信息條件熵H(D|A)之差，即公式為：

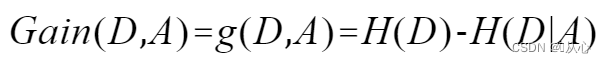
信息熵：

條件熵：（D為訓練數據集所有樣本，A為某一特征，n為特征A的特征值種類，|Di|為第i類數量，

K為所劃分的類別數量，|Dik|第i類劃分為第k類的數量）

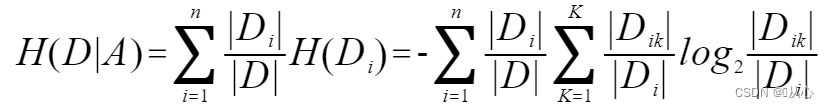
其實就是父節點的信息熵與其下所有子節點總信息熵之差。

2.2.3、栗子

用一個栗子（銀行貸款數據）來理解：eg：

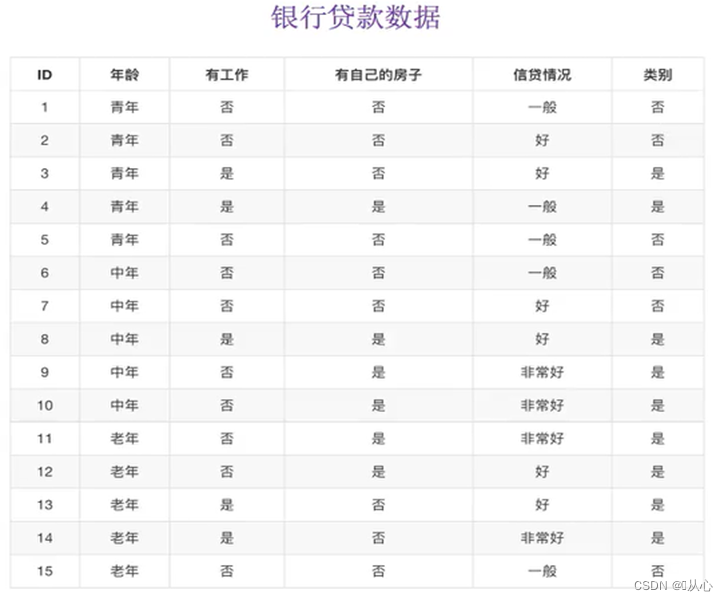
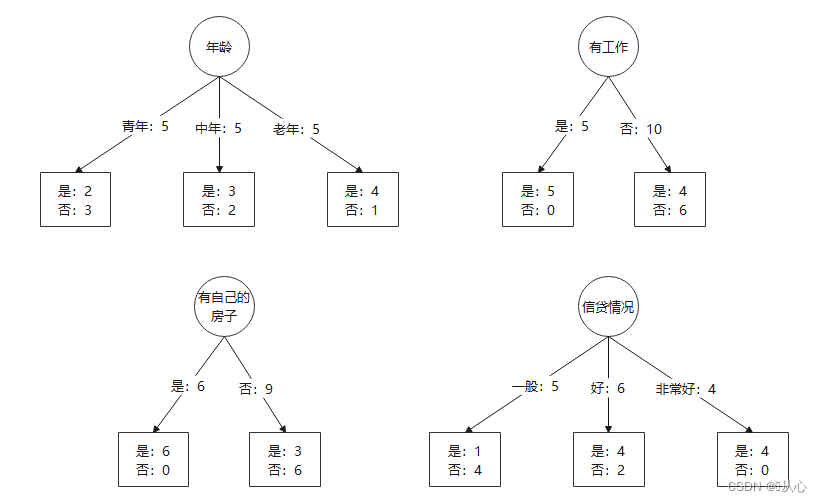?“年齡”信息增益：

“有工作”信息增益：?

“有房子”信息增益：?

?

“信貸情況”信息增益：?

?

對4種特征的Gain進行比較，Gain（D,有房子）≈0.420最大，所以應該選擇“有房子”作為決策樹的根節點。

選擇根節點后，在劃分后的基礎上，在對其他特征遞歸計算，得到下一個Gain最大的特征，以此類推構建一顆決策樹。

2.3、信息增益率（決策樹的劃分依據二）--C4.5

2.3.1、概念

增益率是用前面的增益度量Gain(D，A)和特征A的“固有值”（intrinsic value）的比值來共同定義的。

信息增益率? “信息增益 / 內在信息”‘，會導致屬性的重要性隨著內在信息的增??減?（也就是說，如果這個屬性本身不確定性就很?，那我就越不傾向于選取它），這樣算是對單純?信息增益有所補償。

（信息增益傾向于特征值較多的，信息增益率傾向于特征值較少的）

2.3.2、公式

2.3.3、栗子

還是用上面的例子繼續計算：

“年齡”信息增益率：

“有工作”信息增益率：?

“有房子”信息增益率：?

“信貸情況”信息增益率：?

對4種特征的Gain_ratio進行比較，Gain_ratio（D,有房子）≈0.433最大，所以應該選擇“有房子”作為決策樹的根節點。

選擇根節點后，在劃分后的基礎上，在對其他特征遞歸計算，得到下一個Gain_ratio最大的特征，以此類推構建一顆決策樹。

2.4、基尼值和基尼指數（決策樹的劃分依據三）--CART

CART （Classification and Regression Tree）

2.4.1、基尼值

Gini(D)：從數據集D中隨機抽取兩個樣本，其類別標記不?致的概率。Gini（D）值

越?，數據集D的純度越?。 數據集 D 的純度可?基尼值來度量

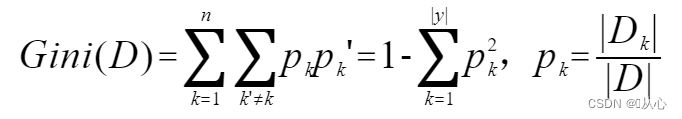
2.4.2、基尼指數

Gini_index(D,A)：?般，選擇使劃分后基尼系數最?的屬性作為最優化分屬性。

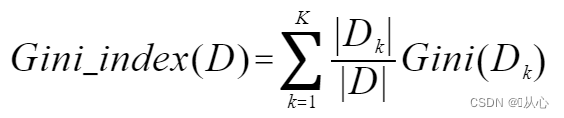
2.4.3、栗子

還是用上面的例子繼續計算：

“年齡”基尼指數：

?“有工作”基尼指數：

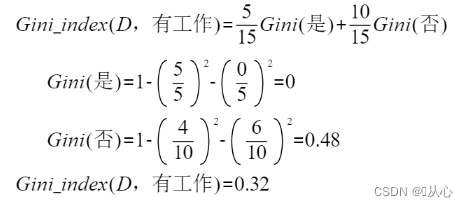
?“有房子”基尼指數：

?“信貸情況”基尼指數：

對4種特征的Gini_index進行比較，Gini_index（D,有房子）≈0.264最低，所以應該選擇“有房子”作為決策樹的根節點。

選擇根節點后，在劃分后的基礎上，在對其他特征遞歸計算，得到下一個Gini_index最小的特征，以此類推構建一顆決策樹。

2.4.4、栗子

針對連續值進行劃分

咱們直接考慮年收入的Gini：

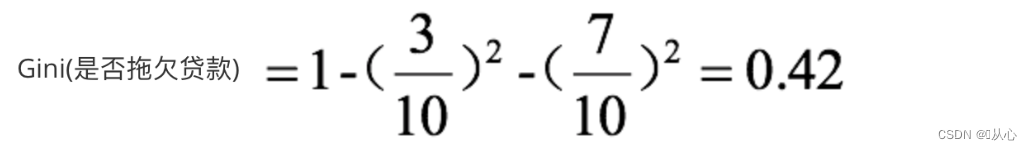
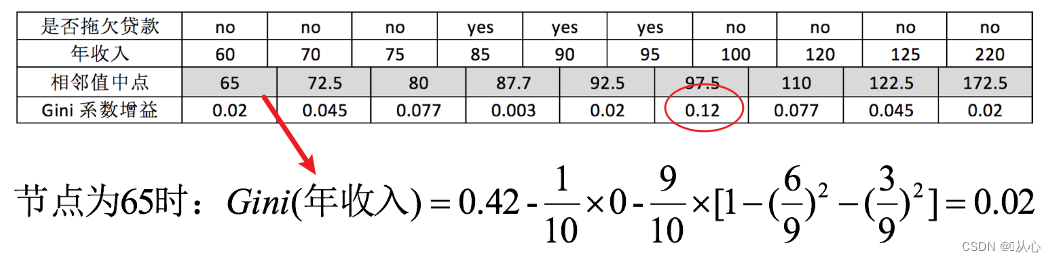
會將每兩個連續年收入取中值進行劃分，并求出其Gini系數增益，從表中可知，將年收入從95，和100處分成兩部分Gini增益最高。

3、cart剪枝

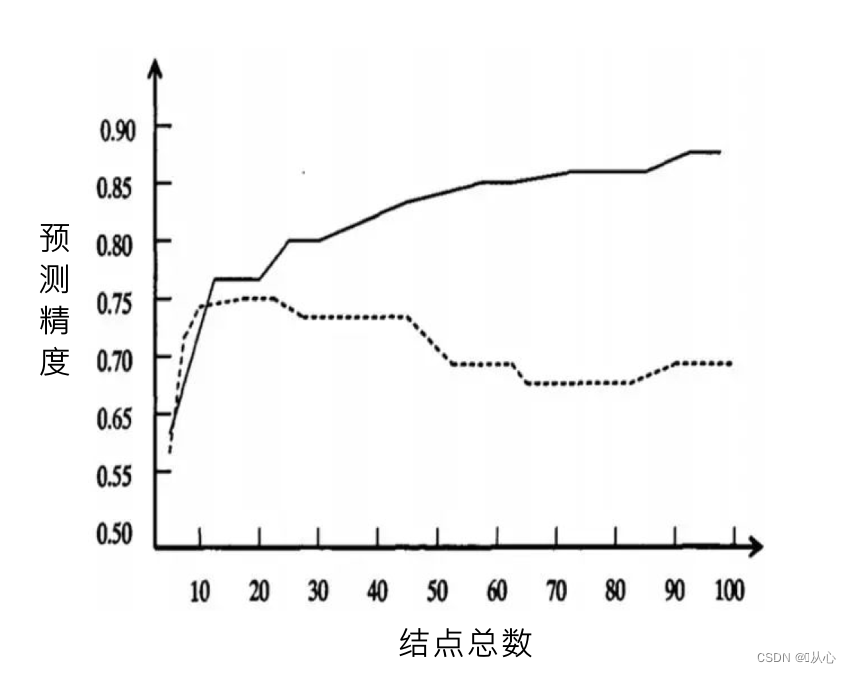
?實線顯示的是決策樹在訓練集上的精度，虛線顯示的則是在一個獨立的測試集上測量出來的精度。

隨著樹的增長，在訓練樣集上的精度是單調上升的， 然而在獨立的測試樣例上測出的精度先上升后下降。

出現這種情況的原因：

? ? ? ? 1、噪聲、樣本沖突，即錯誤的樣本數據。

? ? ? ? 2、特征即屬性不能完全作為分類標準。

? ? ? ? 3、巧合的規律性，數據量不夠大。

2.1、預剪枝

1、每一個結點所包含的最小樣本數目，例如10，則該結點總樣本數小于10時，則不再分；

2、指定樹的高度或者深度，例如樹的最大深度為4；

3、指定結點的熵小于某個值，不再劃分。隨著樹的增長， 在訓練樣集上的精度是單調上升的， 然而在獨立的測試樣例上測出的精度先上升后下降。

2.2、后剪枝

后剪枝，在已生成過擬合決策樹上進行剪枝，可以得到簡化版的剪枝決策樹。

4、優缺點

4.1、ID3

信息增益的缺點是傾向于選擇取值較多的屬性，在有些情況下這類屬性可能不會提供太多有價值的信息.

ID3算法只能對描述屬性為離散型屬性的數據集構造決策樹。

4.2、C4.5

改進：

1. 用信息增益率來選擇屬性
2. 可以處理連續數值型屬性
3. ?采用了一種后剪枝方法
4. 對于缺失值的處理

優點：
????????產生的分類規則易于理解，準確率較高。

? 缺點：
????????在構造樹的過程中，需要對數據集進行多次的順序掃描和排序，因而導致算法的低效。
????????C4.5只適合于能夠駐留于內存的數據集，當訓練集大得無法在內存容納時程序無法運行。

4.3、cart

CART算法相比C4.5算法的分類方法，采用了簡化的二叉樹模型，同時特征選擇采用了近似的基尼系數來簡化計算。

C4.5不一定是二叉樹，但CART一定是二叉樹。

三、**算法實現

四、接口實現

1、API

sklearn.tree.DecisionTreeClassifier導入：
from sklearn.tree import DecisionTreeClassifier語法：
DecisionTreeClassifier(criterion=’gini’, max_depth=None,random_state=None)criterion：劃分標準；{"gini","entropy"},default="gini"max_depth：樹的深度大小;int,default="None"min_samples_split：某節點的樣本數少于min_samples_split，不會繼續再嘗試選擇最優特征來進行劃分;int,default=2min_samples_leaf：限制了葉子節點最少的樣本數，如果某葉子節點數目小于樣本數，則會和兄弟節點一起被剪枝;int,default="None"max_leaf_nodes：限制最大葉子節點數，可以防止過擬合;int,default="None"random_state：隨機數種子 max_features：限制最大特征數;{None,log2,sqrt},default="None"

2、流程

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_splitfrom sklearn.tree import DecisionTreeClassifier

2.1、獲取數據

# 加載數據
iris = load_iris()  

2.2、數據預處理

# 劃分數據集
x_train,x_test,y_train,y_test = train_test_split(iris.data, iris.target, test_size=0.2, random_state=1473) 

2.3、特征工程

2.4、決策樹模型訓練

# 實例化預估器
dtc = DecisionTreeClassifier()  # 確定決策樹參數# 模型訓練
dtc.fit(x_train, y_train) 

2.5、模型評估

# 預測測試集結果
y_pred = dtc.predict(x_test)
print('前20條記錄的預測值為：\n', y_pred[:20])
print('前20條記錄的實際值為：\n', y_test[:20])

# 求出預測準確率和混淆矩陣
from sklearn.metrics import accuracy_score, confusion_matrixprint("預測結果準確率為：", accuracy_score(y_test, y_pred))
print("預測結果混淆矩陣為：\n", confusion_matrix(y_test, y_pred))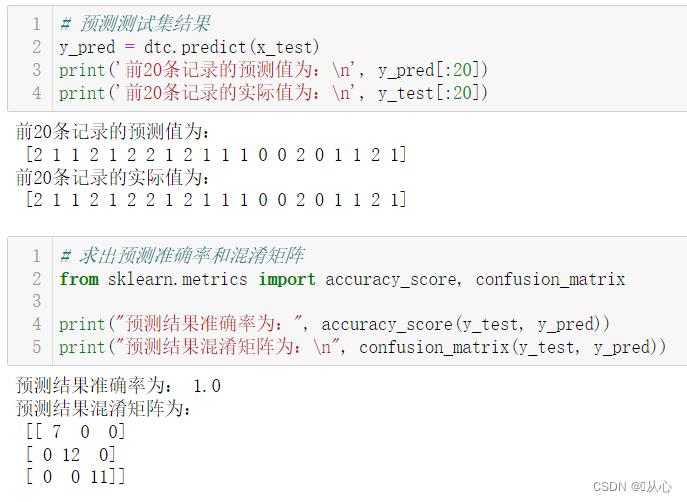

?

2.6、結果預測

經過模型評估后通過的模型可以代入真實值進行預測。

2.7、決策樹可視化

2.7.1、導出dot文件

# 決策樹可視化
from sklearn.tree import export_graphvizexport_graphviz(# 傳入構建好的決策樹模型dtc,# 設置輸出文件（需要設置為 .dot 文件，之后再轉換為 jpg 或 png 文件）out_file="./data/iris_tree.dot", # 設置特征的名稱feature_names=iris.feature_names,# 設置不同分類的名稱（標簽）class_names=iris.target_names
)

2.7.2、下載Graphviz插件

官網：Graphviz官網

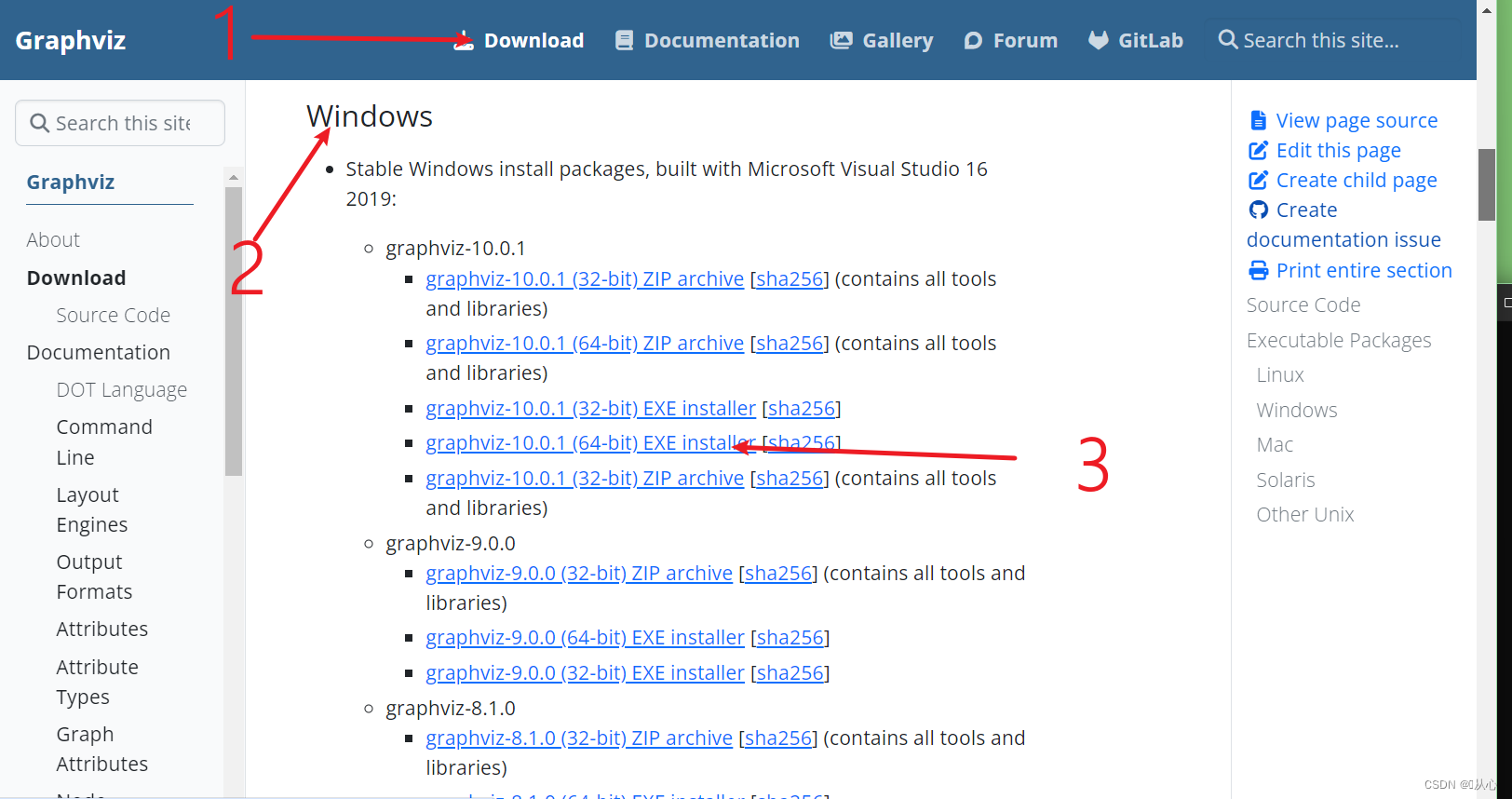
！！！注意：這里一定要把加入系統路徑（環境變量）勾上哦。

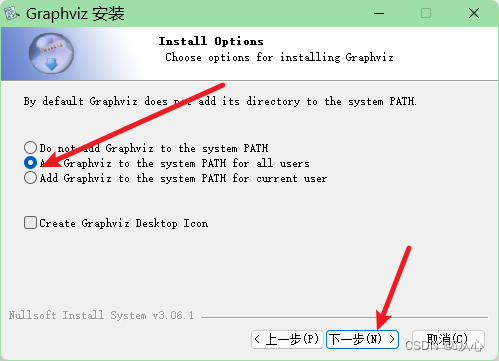
等待安裝完成即可

2.7.3、生成可視化圖片

找到導出的dot文件位置

打開cmd（輸入cmd，回車）

輸入命令

dot -Tpng iris_tree.dot -o iris_tree.png或dot -Tjpg iris_tree.dot -o iris_tree.jpg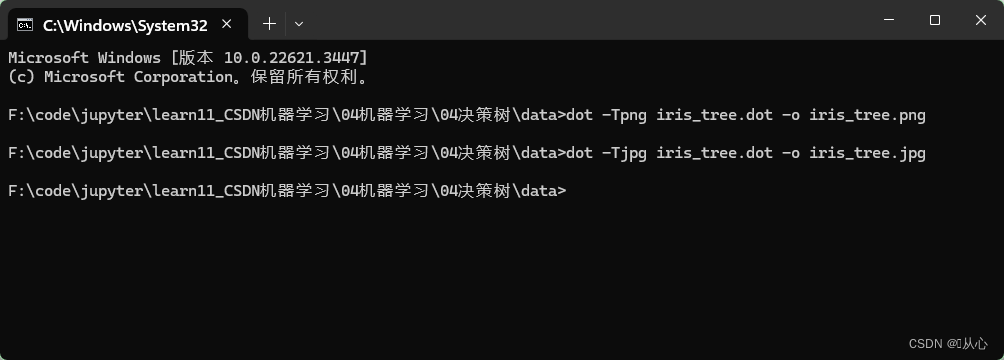

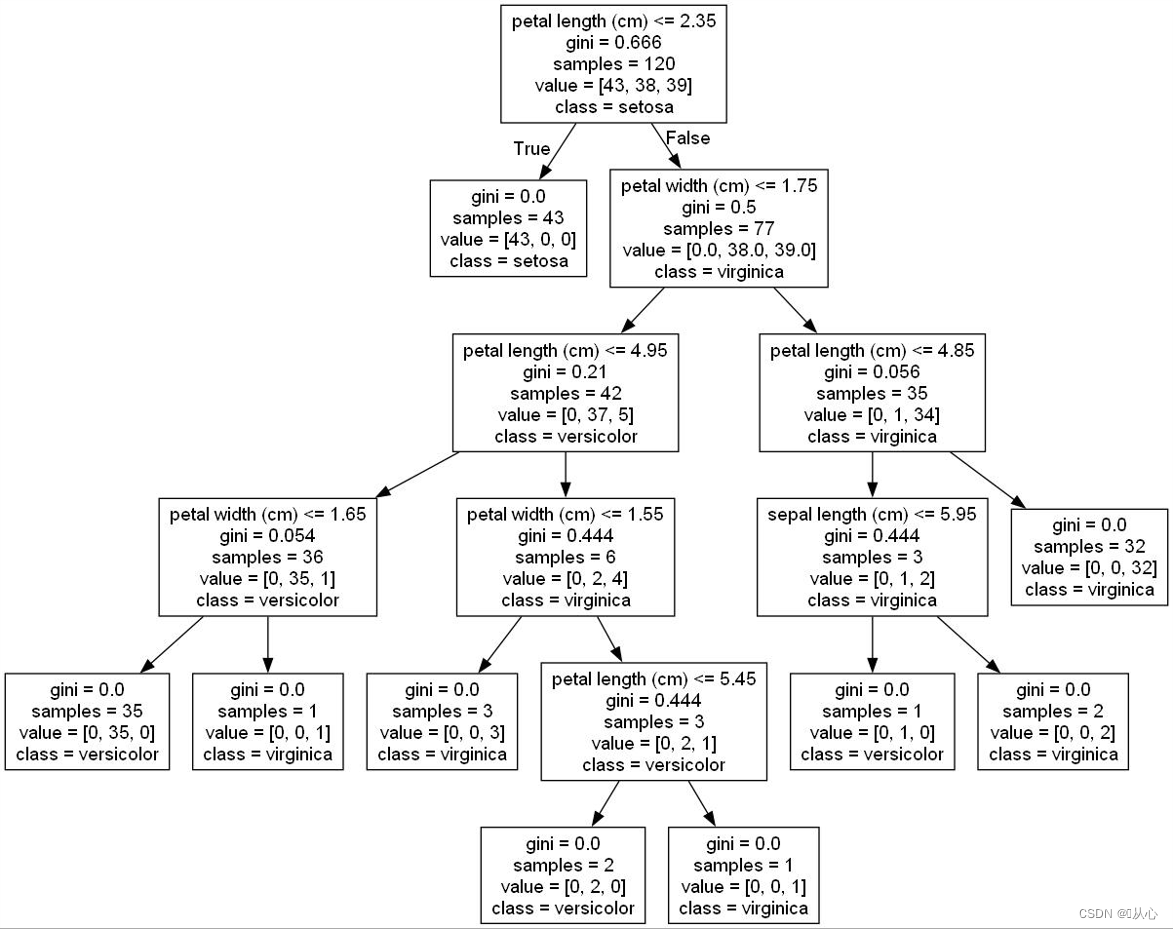
?分析：非葉節點的第一行如petal length(cm)<=2.35，為劃分屬性即條件，如將petal length屬性按照不高于2.35和高于2.35分成兩部分。

gini=0.666，表示該節點的gini值。

samples=120，為總樣本數量。

value=[43,38,39]，為各類別樣本數量。

class=setosa，為該節點被劃分的類別（樣本類別數量最多的類別），葉節點才具有參考價值。

---

舊夢可以重溫，且看：機器學習（五） -- 監督學習（2） -- 樸素貝葉斯
欲知后事如何，且看：?????????機器學習（五） -- 監督學習（4） -- 集成學習方法-隨機森林