前饋神經網絡FNN、多層感知機MLP和反向傳播推導

一、前饋神經網絡FNN

激活函數的使用

二、多層感知機MLP

MLP的典型結構

多層感知機MLP的特點

和前饋神經網絡FNN的區別

三、傳播推導

1、前向傳播(Forward propagation)

（1）輸入層到隱藏層

（2）隱藏層到輸出層

2、反向傳播(Backward propagation)

（1）正向傳播（Forward Pass）

（2）反向傳播（Backward Pass）

① 鏈式求導法則

② 梯度計算

反向傳播算法的作用

具體的推導步驟

總結

三、常見問題

1、如何理解“梯度指向了損失函數增加最快的方向”

2、為何說“最佳參數解的最簡單方式就是微分方程等于0找解”

3、學習率跟誰有關？

一、前饋神經網絡FNN

給定一組神經元，我們可以將神經元作為節點來構建一個網絡。不同的神經網絡模型有著不同網絡連接的拓撲結構。一種比較直接的拓撲結構是前饋網絡。

前饋神經網絡（Feedforward Neural Network，FNN）是最早發明的簡單人工神經網絡。前饋神經網絡也經常稱為多層感知器（Multi-Layer Perceptron，MLP）。但多層感知器的叫法并不是十分合理，因為前饋神經網絡其實是由多層的 Logistic 回歸模型（連續的非線性函數）組成，而不是由多層的感知器（不連續的非線性函數）組成。

在前饋神經網絡中，各神經元分別屬于不同的層。每一層的神經元可以接收前一層神經元的信號，并產生信號輸出到下一層。第0層稱為輸入層，最后一層稱為輸出層，其他中間層稱為隱藏層。整個網絡中無反饋，信號從輸入層向輸出層單向傳播，可用一個有向無環圖表示。

激活函數的使用

在FNN中處理二維矩陣輸入時，激活函數通常作用于每個元素上。也就是說，對于二維矩陣中的每個元素，都會獨立地應用激活函數f。這個過程通常發生在網絡的隱藏層，其中每個神經元接收來自前一層的加權輸入，然后通過激活函數轉換成一個新的矩陣，用作下一層的輸入。

在實際的神經網絡中，隱藏層的每個神經元通常會接收來自前一層所有神經元的加權和，然后通過激活函數。這意味著，雖然激活函數是逐元素應用的，但在計算每個隱藏層神經元的輸出時，會先進行一個線性變換（即 𝑤?𝑥+𝑏，其中 𝑤是權重，𝑏是偏置）。

二、多層感知機MLP

多層感知機（Multilayer Perceptron，MLP）是一種特殊的前饋人工神經網絡，是前饋神經網絡的一個子集。

所有的多層感知機都是前饋神經網絡，但并非所有的前饋神經網絡都是多層感知機。

MLP是機器學習中常見的模型之一，特別是在處理表格數據時。它們在許多領域都有應用，包括分類、模式識別、預測等。然而，MLP也有其局限性，比如容易過擬合，以及對輸入特征的縮放敏感等問題。

MLP的典型結構

輸入層：接收原始數據。
隱藏層：一個或多個層，負責處理輸入層的信息并提取特征。
輸出層：產生最終的預測結果。

多層感知機MLP的特點

至少三層：一個輸入層、至少一個隱藏層和一個輸出層。
全連接：除輸入層外，每一層的所有神經元都與前一層的所有神經元相連。
非線性激活函數：除輸入節點外，每個節點都是一個帶有非線性激活函數的神經元。每個神經元都使用非線性激活函數，如ReLU、sigmoid或tanh。

和前饋神經網絡FNN的區別

復雜性：并非所有的前饋神經網絡需要有多個隱藏層或非線性激活函數。例如，一個只有輸入層和輸出層的網絡，沒有隱藏層，也是一個前饋神經網絡，但不是多層感知機。
通用逼近能力：MLP因其多層結構和非線性激活函數，通常具有更強的學習和逼近復雜函數的能力。
應用范圍：MLP由于其結構和學習能力，常用于分類、模式識別和預測任務，而更簡單的前饋網絡可能用于更特定的任務或作為更復雜網絡架構的一部分。

MLP中，每個連接的權重和偏差都通過訓練過程進行調整，以最小化輸出和目標值之間的差異。這個過程通常涉及大量的計算，因此MLP的實現通常依賴于高效的數學庫和硬件加速。

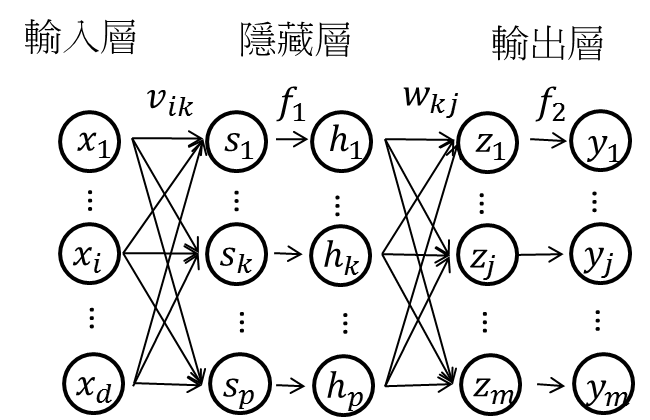
三、傳播推導

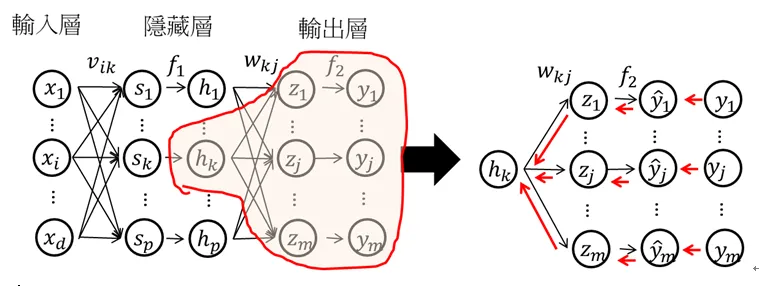
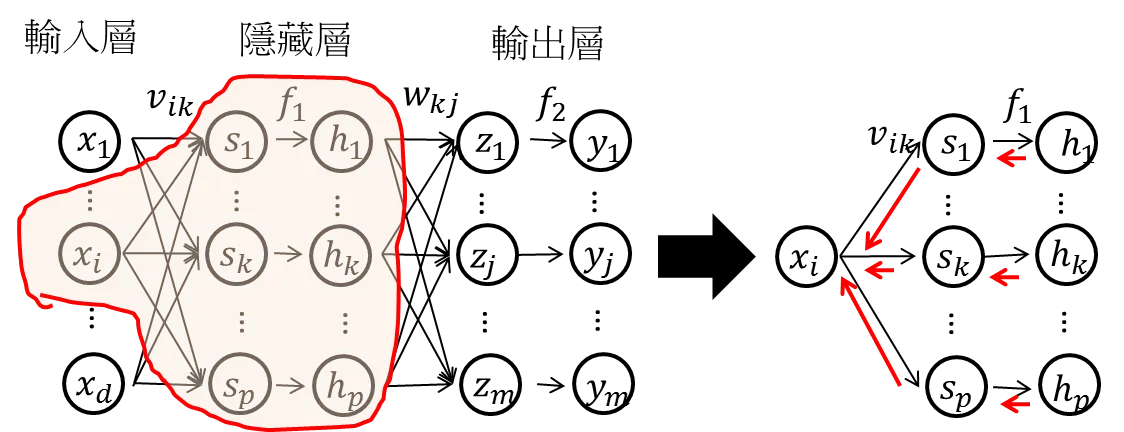
這是一個MLP的結構，共有n個樣本，每個樣本對應m個輸出值。假設隱藏層只有一層，其中隱藏層有p個hidden node。

其中每個輸入的圖片維度為d，則樣本表達形式為：

其中：d為每個輸入樣本的維度，x(i)是一個樣本，總共有n個（對應于樣本個數），m為每個樣本對應的輸出數量。

1、前向傳播(Forward propagation)

（1）輸入層到隱藏層

其中右側是從左側的圖中截取出來的一個運算過程。即輸入層到隱藏層的值為sk,k=1,2,…,p，是輸入層輸入數據的加權線性和。

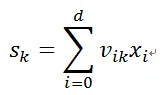
其中：vik是第i個輸入到第k個hidden node的權重。i對應的是輸入值的順序，k對應的是神經元節點的順序。

在隱藏層中，經過非線性轉換（假設激活函數為f1），得到隱藏層的輸出為hk,k=1,2,…,p。

（2）隱藏層到輸出層

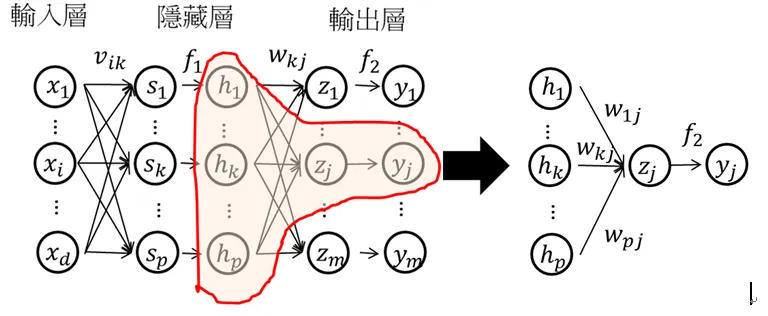
隱藏層到輸出層的值為zj,j=1,2,…,m，是隱藏層輸出hk,k=1,2,…,p的加權線性和。

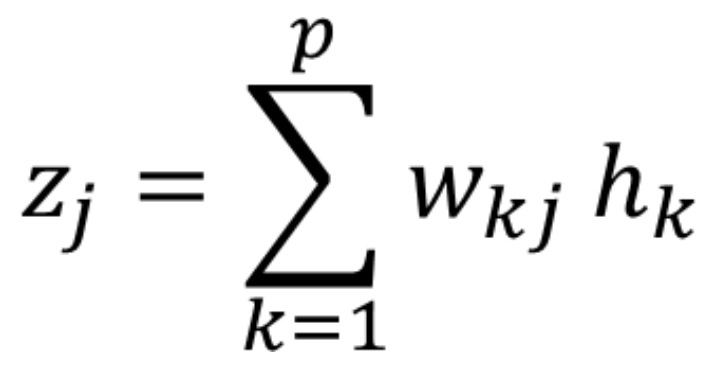
其中：wkj是第k個hidden node輸出到第j個輸出值的權重。

在輸出層中，經過非線性轉換（假設激活函數為f2），得到輸出層的輸出為yj,j=1,2,…,m。

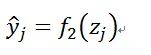
2、反向傳播(Backward propagation)

反向傳播算法是訓練多層神經網絡，特別是前饋神經網絡（如多層感知機）的關鍵算法。它結合了梯度下降法和鏈式求導法則，用于計算網絡中每個參數的梯度，以便通過迭代調整這些參數來最小化網絡的預測誤差。反向傳播算法包括兩個主要的傳播過程：

（1）正向傳播（Forward Pass）

在這個階段，輸入數據通過網絡的多個層次（從輸入層到隱藏層，最后到輸出層）進行處理。在每個層級，數據會通過一個加權求和（包括一個偏置項）并應用一個非線性激活函數。每一層的輸出都是下一層的輸入。在每個神經元中，輸入信號通過加權求和，然后通過一個非線性激活函數進行轉換。

最終，輸出層生成一個預測值，這個值與真實值之間的差異用來衡量網絡的性能。

（2）反向傳播（Backward Pass）

反向傳播階段的目標是找到一種方法來調整網絡中的權重，以減少預測誤差。這個過程從輸出層開始，逆向遍歷網絡的每一層。

在這個階段，算法計算輸出層的預測值和真實值之間的誤差，然后這個誤差會通過網絡反向傳播，直到達到輸入層。在反向傳播過程中，利用鏈式求導法則計算每個權重對最終誤差的貢獻（即梯度），并更新權重以減少誤差。

① 鏈式求導法則

鏈式求導法則是微積分中的一種計算方法，用于計算復合函數的導數。在神經網絡的上下文中，它用于計算損失函數相對于網絡中每個權重的導數。這是因為損失函數（如均方誤差或交叉熵損失）是通過網絡的多個層次復合而成的。

② 梯度計算

梯度是一個向量，其每個元素都是損失函數相對于網絡中某個權重的偏導數。換句話說，梯度指向了損失函數增加最快的方向。在反向傳播算法中，我們計算損失函數相對于每個權重的偏導數，以確定如何調整權重以減少誤差。

反向傳播算法的作用

梯度計算：為每個權重計算誤差梯度，這是權重更新的基礎。
權重更新：利用梯度下降或其他優化算法來更新網絡中的權重和偏置，以減少預測誤差。
損失函數最小化：通過迭代調整權重，反向傳播算法旨在最小化網絡的損失函數，即預測值和真實值之間的差異。
泛化能力提升：通過優化網絡參數，提高模型對未見數據的預測能力，即提升模型的泛化能力。

反向傳播的目的是利用最后的目標函數（loss/cost function）來進行參數的更新，一般來說都是使用誤差均方和（mean square error）當做目標函數。誤差值越大，說明參數學習的不好，還需要繼續學習，直到參數或者誤差值收斂。

具體的推導步驟

計算最終誤差：首先計算輸出層的預測值和真實值之間的誤差，這通常通過損失函數來量化。
應用鏈式求導：然后，利用鏈式求導法則，從輸出層開始，逆向計算每個層的誤差相對于該層輸入的偏導數。這涉及到對激活函數求導以及對權重求導。
計算梯度：通過將這些偏導數與前一層的誤差信號相乘，可以得到每個權重的梯度。
更新權重：最后，使用這些梯度來更新每個權重，通常通過梯度下降法或其他優化算法來實現。權重更新的目的是減少損失函數的值，從而提高網絡的預測準確性。

假設x(i)是第i層的輸入值，其輸出值為：

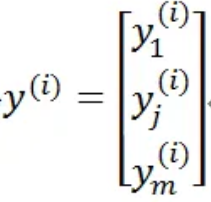
其目標的誤差為：

所有樣本的誤差和當作目標函數：

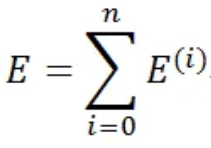
所以要找到最佳參數解（參數只有兩個權重wkj和vik），最簡單的方式就是微分方程等于0找解：

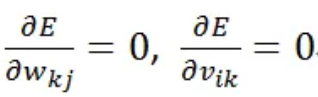
但是當參數量比較多的時候，就不能直接找到唯一解，所以還是要依賴梯度下降（Gradient Descent）找最佳解。

針對上述的兩個參數（wkj和vik）求最佳值：

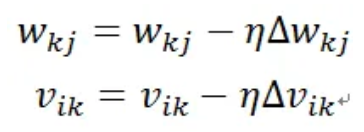
其中 $\eta$ 為學習率(learning rate)：

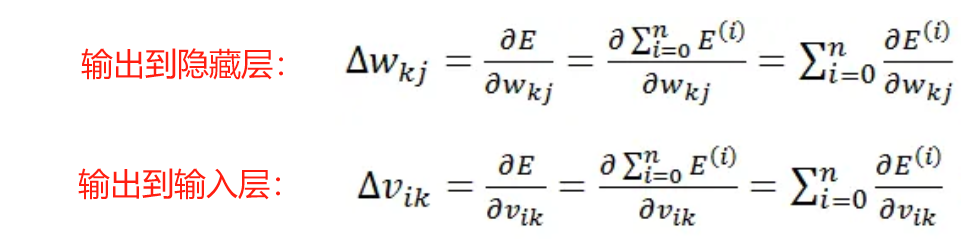
輸出層到隱藏層（權重為wkj）：

鏈式求導（chain rule）:

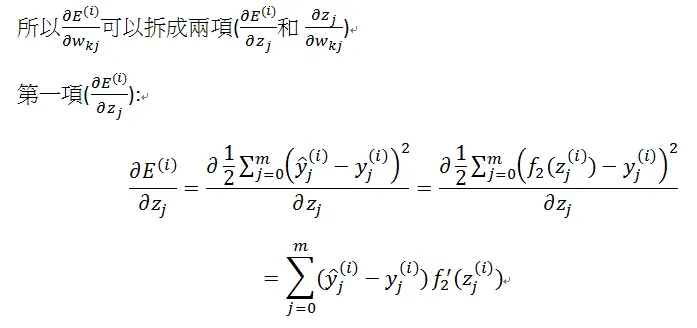
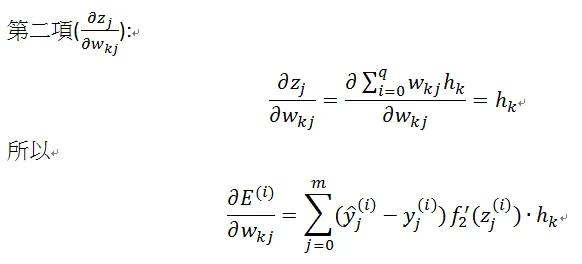
隱藏層到輸入層

隱藏層到輸入層（權重為vik）：

鏈式求導（chain rule）:

所以：

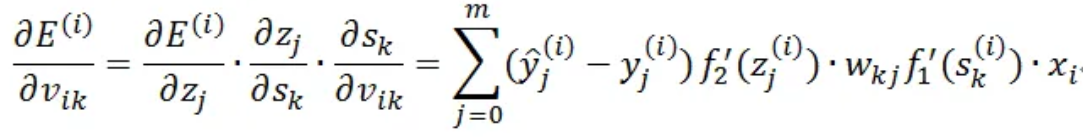
最后把n個樣本所有的梯度（gradient）相加得到參數的更新：

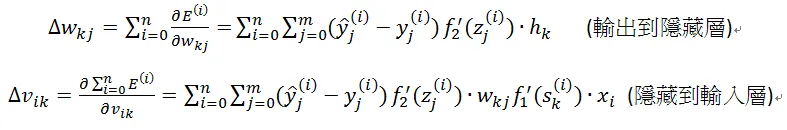
其中需要注意的地方：非線性轉換/激活函數（f1/f2）在反向傳播的時候都有微分，所以在選擇激活函數時必須選擇可微分函數。

總結

MLP是利用梯度下降（gradient descent）求最佳參數解：

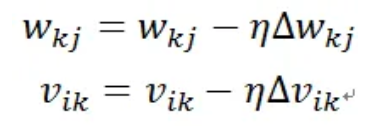
最后代入到MLP內的前向傳播（Forward propagation）即得到最后的預測值。

三、常見問題

1、如何理解“梯度指向了損失函數增加最快的方向”

梯度向量中的每個分量（即偏導數）都表示了在損失函數中，如果沿著該分量對應的維度（也就是權重）增加一個極小的量，損失函數增加的速度。換言之，梯度向量告訴你了損失函數在權重空間中的“最陡峭”的上升方向。

為了深入理解這個概念，可以從以下幾個方面考慮：

多維空間中的“方向”：在多維空間（比如權重空間）中，方向不再像在二維或三維空間中那樣直觀。在這里，“方向”可以用一個向量來表示，這個向量的每個分量對應于空間中的一個維度。
損失函數的曲面：想象損失函數是權重空間中的一個曲面，我們的目標是找到這個曲面的最小值。在曲面上任意一點，都存在一個方向使得曲面上升最快，這個方向就是損失函數在該點的梯度。
梯度下降：在機器學習中，我們通常使用梯度下降算法來優化損失函數。梯度下降的基本思想是沿著梯度的相反方向（即下降方向）移動，因為這樣做可以減少損失函數的值。通過不斷迭代這個過程，我們希望找到損失函數的局部最小值（或者在某些情況下是全局最小值）。
數學表述：梯度 ?𝐽(𝑤)?是損失函數 𝐽(𝑤)關于權重 𝑤的向量導數。如果我們有一個權重向量 𝑤，損失函數 𝐽(𝑤)的梯度可以寫作：

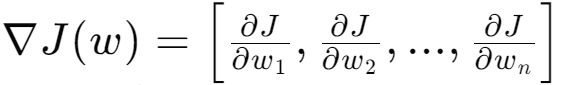
????????其中， $\frac{\partial J}{\partial wi}$ 是損? ? ?失函數相對于第 𝑖i個權重的偏導數。

直觀理解：如果將損失函數想象成一座山，那么梯度向量就指向了這座山“最陡”的地方，也就是上升最快的方向。梯度下降算法就是通過沿著與這個最陡方向相反的方向走，來試圖找到山的底部，即損失函數的最小值。

2、為何說“最佳參數解的最簡單方式就是微分方程等于0找解”

當提到“微分方程等于0找解”時，通常是在談論如何找到損失函數相對于每個權重的偏導數的零點。這個過程是梯度下降算法的一部分，目的是找到損失函數的最小值。

微分方程：在機器學習中，通常不會使用傳統意義上的微分方程，而是使用偏導數的概念。當說“微分方程”時，我們實際上是在談論損失函數相對于權重的偏導數。
偏導數：損失函數 𝐽相對于權重 𝑤𝑘𝑗或 𝑣𝑖𝑘的偏導數表示了當權重 𝑤𝑘𝑗或 𝑣𝑖𝑘增加一個極小量時，損失函數 𝐽的變化率。
等于0：當將損失函數相對于某個權重的偏導數設置為0時，是在尋找損失函數相對于該權重的局部最小值。在理論上，如果偏導數為0，那么在該點附近，損失函數不會隨著權重的增加而增加，這通常意味著找到了一個局部最小點。
求解：在實際操作中，通常不會直接求解偏導數等于0的解析解，因為這樣的解可能很難找到，或者根本不存在。相反，我們使用數值優化方法，如梯度下降，來迭代地調整權重，直到找到損失函數的最小值。

3、學習率跟誰有關？

學習率（learning rate）是一個超參數，它決定了在每次迭代中權重更新的步長。選擇合適的學習率對模型的訓練過程和最終性能至關重要。學習率的選擇通常基于以下幾個方面：

經驗：在實踐中，數據科學家和機器學習工程師會根據經驗來設置學習率。一些常見的初始學習率值在不同的應用領域和問題中被廣泛使用。
文獻推薦：對于某些特定的問題或模型，研究文獻可能會推薦特定的學習率范圍。
網格搜索：可以通過網格搜索（grid search）等超參數調優技術來尋找最佳的學習率。這涉及在一組預定義的學習率值中進行訓練，并選擇產生最佳性能的學習率。
自適應學習率優化器：一些優化算法，如Adam（Adaptive Moment Estimation）、RMSprop（Root Mean Square Propagation）或AdaGrad（Adaptive Gradient），能夠自動調整學習率，使得訓練過程更加高效。
學習率衰減（Learning Rate Decay）：在訓練過程中逐漸減小學習率是一種常見的做法。這可以通過多種方式實現，例如，隨著時間的增加線性或指數衰減學習率。
實驗：最終，確定最佳學習率通常需要實驗。可以通過多次訓練實驗，每次使用不同的學習率，然后選擇在驗證集上表現最好的學習率。
自動化超參數優化工具：使用如Hyperopt、Optuna或Ray Tune等工具可以自動化超參數搜索過程，包括學習率的優化。
問題規模：問題的規模有時也會影響學習率的選擇。對于大規模問題，可能需要較小的學習率以避免訓練過程中的不穩定。
損失函數的性質：損失函數的平滑性和曲率也會影響學習率的選擇。如果損失函數非常崎嶇，可能需要較小的學習率以避免錯過最小值。