模擬集成電路(3)----單級放大器(共源極)
放大是模擬電路的基本功能
- 大多數自然模擬信號太小而無法處理
- 需要足夠的信噪比
理想的放大器
-
線性:無限的幅度和頻率范圍
-
輸入阻抗無限大
-
輸出阻抗無限小
共源放大器
共源放大器就是將源極接AC ground。

一般我們對三點進行分析:
- 直流擺幅有多大(飽和區)
- 小信號的增益
- 輸入輸出的阻抗
電阻負載

大信號分析
- V i n < V T H , c u t o f f V_{in}<V_{TH},\mathrm{~cut~off} Vin?<VTH?,?cut?off
V o u t = V D D V_{out}=V_{DD} Vout?=VDD?
- V i n ? V T H ≤ V o u t , saturation V_{in}-V_{TH}\leq V_{out,}\text{saturation} Vin??VTH?≤Vout,?saturation(一般只考慮飽和區)
V o u t = V D D ? I d ? R D = V D D ? μ n C o x 2 W L ( V i n ? V T H ) 2 ? R D \begin{aligned}&V_{out}=V_{DD}-I_{d}\cdot R_{D}\\&=V_{DD}-\frac{\mu_{n}C_{ox}}{2}\frac{W}{L}(V_{in}-V_{TH})^{2}\cdot R_{D}\end{aligned} ?Vout?=VDD??Id??RD?=VDD??2μn?Cox??LW?(Vin??VTH?)2?RD??
- V i n ? V T H > V o u t , triode V_{in}-V_{TH}>V_{out,}\text{triode} Vin??VTH?>Vout,?triode
小信號增益
大信號的斜率就是小信號的增益
V o u t = V D D ? μ n C o x 2 W L ( V i n ? V T H ) 2 ? R D V_{out}=V_{DD}-\frac{\mu_{n}C_{ox}}{2}\frac{W}{L}\left(V_{in}-V_{TH}\right)^{2}\cdot R_{D} Vout?=VDD??2μn?Cox??LW?(Vin??VTH?)2?RD?
A v = ? V o u t ? V i n = ? μ n C o x W L ( V i n ? V T H ) ? R D A_{v}=\frac{\partial V_{out}}{\partial V_{in}}=-\boxed{\mu_{n}C_{ox}\frac{W}{L}(V_{in}-V_{TH})}\cdot R_{D} Av?=?Vin??Vout??=?μn?Cox?LW?(Vin??VTH?)??RD?
框出的部分即為跨導
A v = ? V o u t ? V i n = ? g m ? R D A_v=\frac{\partial V_{out}}{\partial V_{in}}=-\boxed{g_m}\cdot R_D Av?=?Vin??Vout??=?gm???RD?
發現,不同的 V i n V_{in} Vin?的值會影響增益的值,
- 小信號等效電路
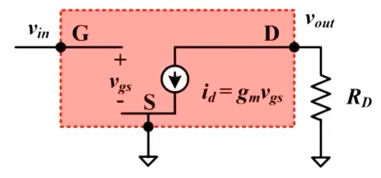
{ ν o u t = ? i d R D i d = g m ν i n \begin{cases} \begin{aligned}&\nu_{out}=-i_{d}R_{D}\\&i_{d}=g_{m}\nu_{in}\end{aligned} \end{cases} {?νout?=?id?RD?id?=gm?νin???
A ν = ν o u t ν i n = ? g m R D A_{\nu}=\frac{\nu_{out}}{\nu_{in}}=-g_{m}R_{D} Aν?=νin?νout??=?gm?RD?
- 考慮溝道長度調制效應

{ ν o u t = ? i d ( R D ∥ r o ) i d = g m ν i n \begin{cases} \begin{aligned}&\nu_{out}=-i_{d}(R_{D}\parallel r_{o})\\&i_{d}=g_{m}\nu_{in}\end{aligned} \end{cases} {?νout?=?id?(RD?∥ro?)id?=gm?νin???
根據常識有 R D ? r o R_D \ll r_o RD??ro?
A ν = ? g m ? ( R D ∥ r o ) ≈ ? g m ? R D \begin{aligned}A_{\nu}&=-g_{m}\cdot(R_{D}\parallel r_{o})\\&\approx-g_{m}\cdot R_{D}\end{aligned} Aν??=?gm??(RD?∥ro?)≈?gm??RD??
輸入輸出阻抗
r i n = ν i n i i n = ∞ r_{in}=\frac{\nu_{in}}{i_{in}}=\infty rin?=iin?νin??=∞
r o u t = r o ∥ R D ≈ R D r_{out}=r_{o}\parallel R_{D}\approx R_{D} rout?=ro?∥RD?≈RD?

V D S = V i n 1 ? V T H V_{\mathrm{DS}}=V_{\mathrm{in}1}-V_{\mathrm{TH}} VDS?=Vin1??VTH?
V i n 1 ? V T H = V D D ? μ n C o x 2 W L ( V i n 1 ? V T H ) 2 ? R D V_{\mathrm{in1}}-V_{\mathrm{TH}}=V_{\mathrm{DD}}-\frac{\mu_{\mathrm{n}}C_{\mathrm{ox}}}{2}\frac{W}{L}(V_{\mathrm{in1}}-V_{\mathrm{TH}})^{2}\cdot R_{\mathrm{D}} Vin1??VTH?=VDD??2μn?Cox??LW?(Vin1??VTH?)2?RD?
可以得到 V i n 1 V_{in1} Vin1?是 R D R_D RD?的一個函數。
R D R_D RD?越大會導致 V i n 1 V_{in1} Vin1?越小

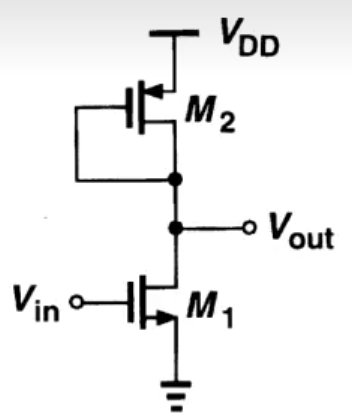
二極管接法負載


在M1和M2的電流是一樣的,于是我們可以列出如下等式:

1 2 μ n C o x ( W L ) 1 ( V i n ? V T H 1 ) 2 = 1 2 μ n C o x ( W L ) 2 ( V D D ? V o u t ? V T H 2 ) 2 \begin{aligned}&\frac{1}{2}\mu_{n}C_{ox}\left(\frac{W}{L}\right)_{1}\left(V_{in}-V_{TH1}\right)^{2}\\&=\frac{1}{2}\mu_{n}C_{ox}\left(\frac{W}{L}\right)_{2}\left(V_{DD}-V_{out}-V_{TH2}\right)^{2}\end{aligned} ?21?μn?Cox?(LW?)1?(Vin??VTH1?)2=21?μn?Cox?(LW?)2?(VDD??Vout??VTH2?)2?
( W L ) 1 ( V i n ? V T H 1 ) = ( W L ) 2 ( V D D ? V o u t ? V T H 2 ) \sqrt{\left(\frac{W}{L}\right)_{1}}(V_{in}-V_{TH1})=\sqrt{\left(\frac{W}{L}\right)_{2}}(V_{DD}-V_{out}-V_{TH2}) (LW?)1??(Vin??VTH1?)=(LW?)2??(VDD??Vout??VTH2?)
可得 V i n V_{in} Vin?和 V o u t V_{out} Vout?幾乎是一個線性關系,如果兩個晶體管的 V T H V_{TH} VTH?不變,那么可以認作是線性關系。
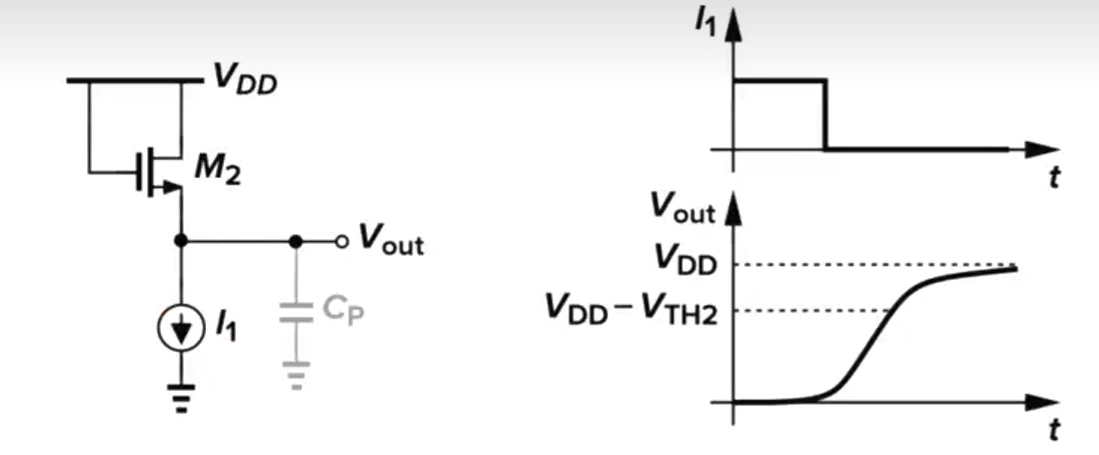
由于有電容的存在,所以 V o u t V_{out} Vout?并不是直接變大。
大信號分析
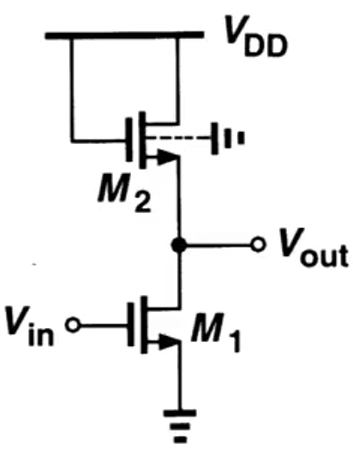
小信號增益
( W L ) 1 ( V i n ? V T H 1 ) = ( W L ) 2 ( V D D ? V o u t ? V T H 2 ) \sqrt{\left(\frac{W}{L}\right)_{1}}(V_{in}-V_{TH1})=\sqrt{\left(\frac{W}{L}\right)_{2}}(V_{DD}-V_{out}-V_{TH2}) (LW?)1??(Vin??VTH1?)=(LW?)2??(VDD??Vout??VTH2?)
( W L ) 1 = ( W L ) 2 ( ? ? V o u t ? V i n ? ? V T H 2 ? V i n ) \sqrt{\left(\frac{W}{L}\right)_1}=\sqrt{\left(\frac{W}{L}\right)_2}(-\frac{\partial V_{out}}{\partial V_{in}}-\boxed{ \frac{\partial V_{TH2}}{\partial V_{in}}}) (LW?)1??=(LW?)2??(??Vin??Vout????Vin??VTH2???)
框住的為 M 2 M_2 M2?的體效應
? V T H 2 ? V i n = ? V T H 2 ? V o u t ? ? V o u t ? V i n = η ? ? V o u t ? V i n \frac{\partial V_{TH2}}{\partial V_{in}}=\frac{\partial V_{TH2}}{\partial V_{out}}\cdot\frac{\partial V_{out}}{\partial V_{in}}=\eta\cdot\frac{\partial V_{out}}{\partial V_{in}} ?Vin??VTH2??=?Vout??VTH2????Vin??Vout??=η??Vin??Vout??
得到增益:
A ν = ? V o u t ? V i n = ? ( W / L ) 1 ( W / L ) 2 ? 1 1 + η A_{\nu}=\frac{\partial V_{out}}{\partial V_{in}}=-\sqrt{\frac{\left(W/L\right)_{1}}{\left(W/L\right)_{2}}}\cdot\frac{1}{1+\eta} Aν?=?Vin??Vout??=?(W/L)2?(W/L)1????1+η1?
小信號模型
小信號模型增益

i x = v x / r o + g m v 1 v 1 = v x } → r e q = v x i x = r o ∥ 1 g m ≈ 1 g m \begin{aligned}&i_{x}=v_{x}/r_{o}+g_{m}v_{1}\\&v_{1}=v_{x}\end{aligned}\biggr\}\to r_{eq}=\frac{v_{x}}{i_{x}}=r_{o}\parallel\frac{1}{g_{m}}\approx\frac{1}{g_{m}} ?ix?=vx?/ro?+gm?v1?v1?=vx??}→req?=ix?vx??=ro?∥gm?1?≈gm?1?
- 考慮體效應

i x = v x r o + ( g m 2 + g m b 2 ) v x i_x=\frac{v_x}{r_o}+(g_{m2}+g_{mb2})v_x ix?=ro?vx??+(gm2?+gmb2?)vx?
r e q = v x i x = r o ∥ 1 g m 2 + g m b 2 ≈ 1 g m 2 + g m b 2 = 1 ( 1 + η ) g m 2 r_{eq}=\frac{v_{x}}{i_{x}}=r_{o}\parallel\frac{1}{g_{m2}+g_{mb2}}\approx\frac{1}{g_{m2}+g_{mb2}}=\frac{1}{(1+\eta)g_{m2}} req?=ix?vx??=ro?∥gm2?+gmb2?1?≈gm2?+gmb2?1?=(1+η)gm2?1?
- 用小信號的方法計算增益

A v = ? g m 1 ? ( r e q ∥ r o 1 ) ≈ ? g m 1 ? r e q A_v=-g_{m1}\cdot(r_{eq}\parallel r_{o1})\approx-g_{m1}\cdot r_{eq} Av?=?gm1??(req?∥ro1?)≈?gm1??req?
A v = ? g m 1 g m 2 ? 1 1 + η A_{v}=-\frac{g_{m1}}{g_{m2}}\cdot\frac{1}{1+\eta} Av?=?gm2?gm1???1+η1?
對于PMOS
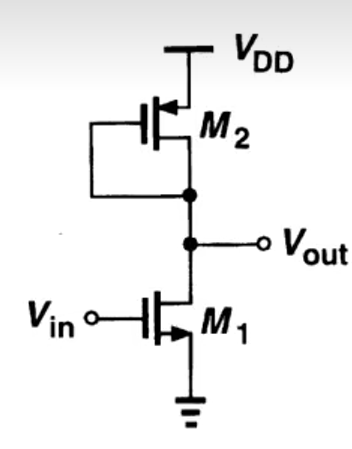
A v = ? g m 1 g m 2 A v = ? μ n ( W / L ) 1 μ p ( W / L ) 2 A_{v}=-\frac{g_{m1}}{g_{m2}}\\A_{v}=-\sqrt{\frac{\mu_{n}(W/L)_{1}}{\mu_{p}(W/L)_{2}}} Av?=?gm2?gm1??Av?=?μp?(W/L)2?μn?(W/L)1???
輸入輸出電阻

r i n = ∞ r_{in}=\infty rin?=∞
r o u t = r o 1 ∥ r o 2 ∥ 1 g m 2 ( 1 + η ) ≈ 1 g m 2 ( 1 + η ) \begin{aligned}r_{out}&=r_{o1}\parallel r_{o2}\parallel\frac{1}{g_{m2}(1+\eta)}\\&\approx\frac{1}{g_{m2}(1+\eta)}\end{aligned} rout??=ro1?∥ro2?∥gm2?(1+η)1?≈gm2?(1+η)1??
r i n = ∞ r_{in}=\infty rin?=∞
r o u t = r o 1 ∥ r o 2 ∥ 1 g m 2 ≈ 1 g m 2 \begin{aligned}r_{out}&=r_{o1}\parallel r_{o2}\parallel\frac{1}{g_{m2}}\\&\approx\frac{1}{g_{m2}}\end{aligned} rout??=ro1?∥ro2?∥gm2?1?≈gm2?1??
電流源負載
一般我們的電流源會用mos管實現,例如pmos
如下是pmos作電流源負載:

M1小信號模型如下:

所以總的小信號模型就是在 r o 1 r_{o1} ro1?并上 r o 2 r_{o2} ro2?
A v = ? g m ? ( r o 1 ∥ r o 2 ) r i n = ∞ r o u t = r o 1 ∥ r o 2 A_{v}=-g_{m}\cdot(r_{o1}\parallel r_{o2})\\r_{in}=\infty\quad r_{out}=r_{o1}\parallel r_{o2} Av?=?gm??(ro1?∥ro2?)rin?=∞rout?=ro1?∥ro2?
電流源負載和電阻負載進行對比:

所以電流源負載可實現小電流實現大增益。
通用的CS分析方法
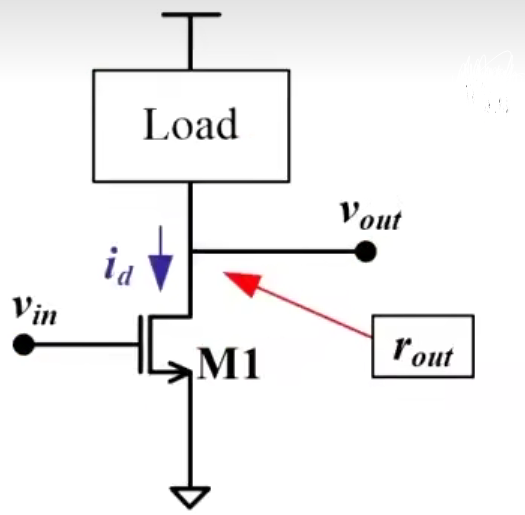
v i n → i d = g m v i n v → i → i d → v o u t = ? i d r o u t i → v ν o u t v_{in}\xrightarrow{i_{d}=g_{m}v_{in}}_{v\to i}\to i_{d}\xrightarrow{v_{out}=-i_{d}r_{out}}_{i\to v}\nu_{out} vin?id?=gm?vin??v→i?→id?vout?=?id?rout??i→v?νout?
v o u t = ? i d r o u t = ? g m v i n r o u t A v = v o u t / v i n = ? g m r o u t v_{out}=-i_{d}r_{out}=-g_{m}v_{in}r_{out}\\A_{v}=v_{out}/v_{in}=-g_{m}r_{out} vout?=?id?rout?=?gm?vin?rout?Av?=vout?/vin?=?gm?rout?
r o u t = r O ∥ r L o a d r_{out}=r_{O}\parallel r_{Load} rout?=rO?∥rLoad?

有源負載的共源極
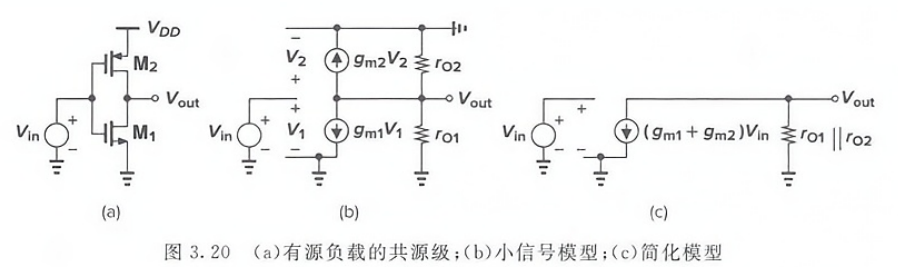
v o u t v i n = ? ( g m l + g m 2 ) ( r o l ∥ r o 2 ) \frac{v_{\mathrm{out}}}{v_{\mathrm{in}}}=-(g_{\mathrm{ml}}+g_{\mathrm{m2}})(r_{\mathrm{ol}}\parallel r_{\mathrm{o2}}) vin?vout??=?(gml?+gm2?)(rol?∥ro2?)
帶源極負反饋的共源級
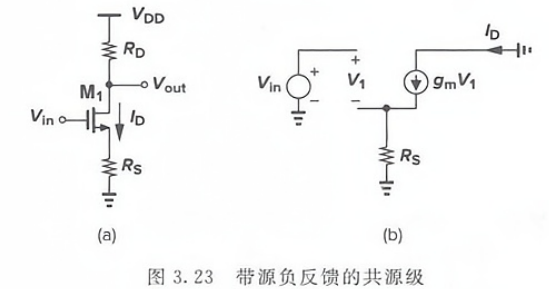
A s s u m i n g λ = γ = 0 Assuming \lambda=\gamma=0 Assumingλ=γ=0
I d = 1 2 μ n C o x W L ( V g s ? V T H ) 2 = 1 2 μ n C o x W L ( V i n ? R S I d ? V T H ) 2 \begin{aligned} I_{d}& =\frac{1}{2}\mu_{n}C_{ox}\frac{W}{L}\big(V_{gs}-V_{TH}\big)^{2} \\ &=\frac12\mu_nC_{ox}\frac WL(V_{in}-R_SI_d-V_{TH})^2 \end{aligned} Id??=21?μn?Cox?LW?(Vgs??VTH?)2=21?μn?Cox?LW?(Vin??RS?Id??VTH?)2?
等效跨導如下:
G m = ? I d ? V i n G_m=\frac{\partial I_d}{\partial V_{in}} Gm?=?Vin??Id??
G m = ? I d ? V i n = μ n C o x W L ( V i n ? R S I d ? V T H ) ( 1 ? R S G m ) G_{m}=\frac{\partial I_{d}}{\partial V_{in}}=\boxed{\mu_{n}C_{ox}\frac{W}{L}(V_{in}-R_{S}I_{d}-V_{TH})}(1-R_{S}G_{m}) Gm?=?Vin??Id??=μn?Cox?LW?(Vin??RS?Id??VTH?)?(1?RS?Gm?)
框住的部分是 g m g_m gm?
G m = g m ( 1 ? R S G m ) ? G m = g m 1 + g m R S G_{m}=g_{m}(1-R_{S}G_{m})\longrightarrow \quad G_{m}=\frac{g_{m}}{1+g_{m}R_{S}} Gm?=gm?(1?RS?Gm?)?Gm?=1+gm?RS?gm??
A ν = ? G m R D = ? g m R D 1 + g m R S A_{\nu}=-G_{m}R_{D}=-\frac{g_{m}R_{D}}{1+g_{m}R_{S}} Aν?=?Gm?RD?=?1+gm?RS?gm?RD??
I f R s is?large?enough? → G m ≈ 1 / R s , A v = R D / R s \mathrm{If~}R_s\text{ is large enough }\to G_m{\approx}1/R_s,A_v{=}R_D/R_s If?Rs??is?large?enough?→Gm?≈1/Rs?,Av?=RD?/Rs?
小信號分析

v 1 = v i n ? v x ν x = ? v b s = R S i o u t v_{1}=v_{in}-v_{x}\quad\nu_{x}=-v_{bs}=R_{S}i_{out} v1?=vin??vx?νx?=?vbs?=RS?iout?













Web應用中web.xml文件中可以配置哪些內容)
)


)

