決策樹是一種基于特征分割的監督學習算法，通過遞歸分割數據空間來構建預測模型。

1.1、決策樹模型基本原理

決策樹思想的來源樸素，程序設計中的條件分支結構就是 if-then結構，最早的決策樹就是利用這類結構分割數據的一種分類學習方法。為了更好理解決策樹具體怎么分類的，我們通過以下問題例子?

問題：如何對這些客戶進行分類預測？你是如何去劃分？我們怎么知道這些特征哪個更好放在最上面，那么決策樹的真是劃分是這樣的。

1.2、決策樹模型的建樹依據

為了易于生成決策樹的理解，下面我們使用“信息熵”來說明決策樹的構建。

1.2.1、信息熵

       需要用到信息論專業的知識！此處，通過經典“猜冠軍”的例子來引入信息熵：

       我們玩個猜測類游戲，猜猜下圖32支球隊那支是冠軍。并且猜測錯誤會付出代價，每猜錯一次給一塊錢，告訴我是否猜對了，那么我需要掏多少錢才能知道誰是冠軍呢？ （這有個前提是：你不知道任意球隊的信息、歷史比賽記錄、球隊實力等）。

為了使代價最小，可以使用二分法來猜測：我可以把球依次編上號，從1到32，然后提問：冠 軍在1-16號嗎？依次詢問，只需要五次，就可以知道結果。

 我們來看這個式子：

• 32支球隊，log32=5比特
• 64支球隊，log64=6比特

香農指出，它的準確信息量應該是，p為每個球隊獲勝的概率（假設概率相等，都為1/32），我們不用錢去衡量這個代價了，香濃指出用比特：

1.2.1.1、信息熵的定義

信息熵（Information Entropy）是信息論中的專業術語，其標準單位為比特（bit），用于衡量系統混亂程度的指標。對于一個離散隨機變量 X，其可能的取值為 x1?,x2…,xn?，應的概率為P(x1?),P(x2?),…,P(xn?)，則信息熵 H(X)（單位為比特）定義為：

“誰是世界杯冠軍”的信息量應該比5比特少，特點（重要）：

• 當這32支球隊奪冠的幾率相同時，對應的信息熵等于5比特
• 只要概率發生任意變化，信息熵都比5比特大

1.2.1.2、總結

信息和消除不確定性是相聯系的：當我們得到的額外信息（球隊歷史比賽情況等等）越多的話，那么我們猜測的代價越小（猜測的不確定性減小）

• 當所有事件等概率時（最大不確定性），熵值最大，需要更多比特來編碼，對應系統混亂，純度低。

• 當某個事件必然發生時（無不確定性），熵值為0，不需要任何比特編碼（因為結果已知)，對應系統穩定，純度高。

import numpy as np
# 計算信息熵?例
p = np.array([39, 37, 44]) / 120 # 概率分布
entropy = -(p * np.log2(p)).sum()
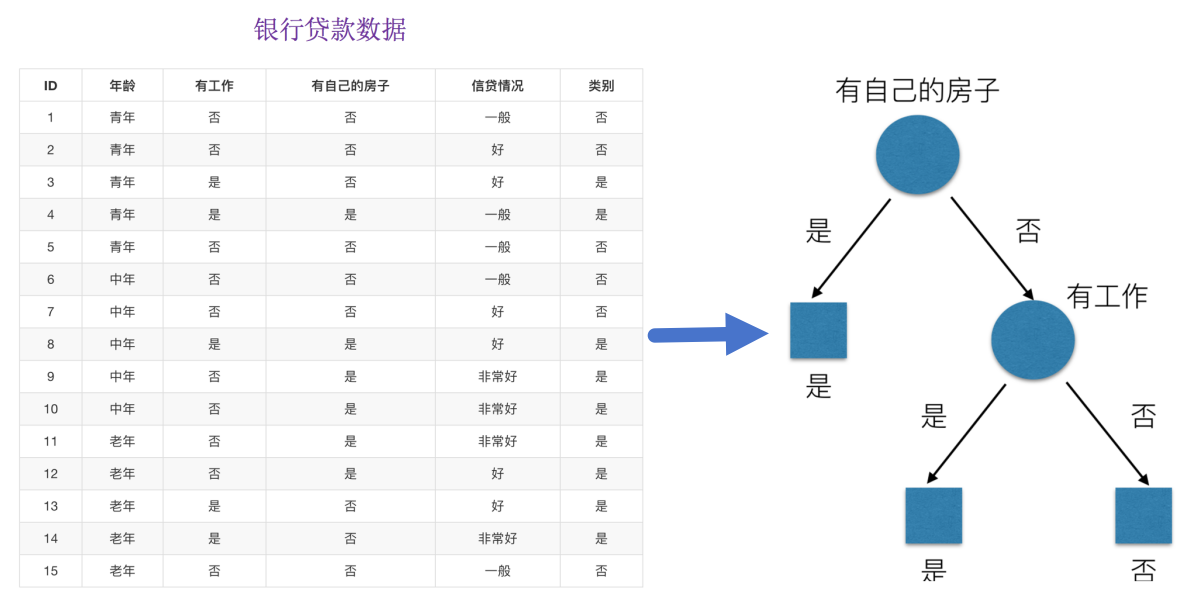
print(f"信息熵: {entropy:.4f}")

問題： 回到我們之前的貸款案例，怎么去劃分？可以利用當得知某個特征（比如是否有房子）之后，我們能夠減少的不確定性大小。越大我們可以認為這個特征很重要。那怎么去衡量減少的不確定性大小呢?

1.2.2 、信息增益(樹劃分依據之一)

1.2.2.1 、定義與公式

特征A對訓練數據集D的信息增益g(D,A)，定義為集合D的信息熵H(D)與特征A給定條件下D的信息條件熵H(D|A)之差，即公式為：

H(D)-數據集D的信息熵（經驗熵）：

• K：目標變量中的類別數量