2025.9.5

226. 翻轉二叉樹

題目

給你一棵二叉樹的根節點 root ，翻轉這棵二叉樹，并返回其根節點。

示例 1：

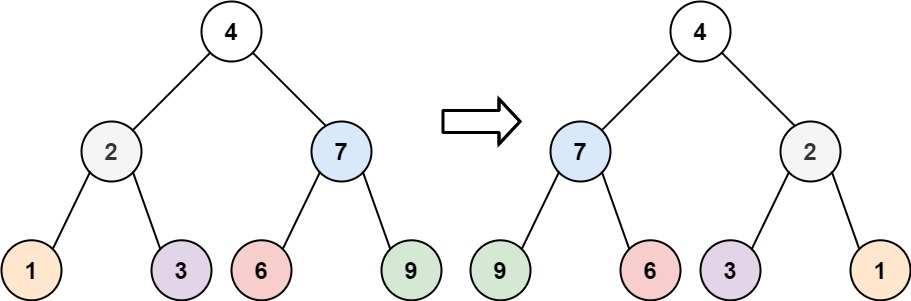
輸入：root = [4,2,7,1,3,6,9]
輸出：[4,7,2,9,6,3,1]

示例 2：

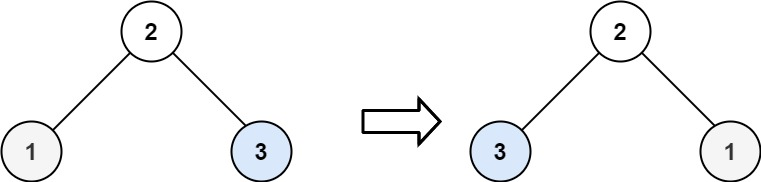
輸入：root = [2,1,3]
輸出：[2,3,1]

示例 3：

輸入：root = []
輸出：[]

提示：

樹中節點數目范圍在 [0, 100] 內
-100 <= Node.val <= 100

總體思路

使用遞歸的深度優先搜索 DFS方法來翻轉二叉樹。其核心思想是：

1. 遞歸地翻轉左子樹
2. 遞歸地翻轉右子樹
3. 交換當前節點的左右子節點
4. 基礎情況：當節點為空時，直接返回（遞歸終止條件）

這種后序遍歷的方式確保在交換當前節點的子節點之前，其左右子樹都已經被正確翻轉。

時間復雜度與空間復雜度

時間復雜度：O(n)

• 每個節點恰好被訪問一次，n為二叉樹中的節點數量
• 每個節點進行常數時間的操作（交換指針）

空間復雜度：O(h)，其中h是樹的高度

• 空間復雜度主要由遞歸調用棧的深度決定
• 在最壞情況下（樹退化為鏈表），h = n，空間復雜度為O(n)
• 在最好情況下（平衡二叉樹），h = logn，空間復雜度為O(logn)
• 平均情況下，空間復雜度為O(h)

代碼

golang

/*** Definition for a binary tree node.* type TreeNode struct {*     Val int*     Left *TreeNode*     Right *TreeNode* }*/
func invertTree(root *TreeNode) *TreeNode {if root == nil {return root}root.Left = invertTree(root.Left)root.Right = invertTree(root.Right)root.Left, root.Right = root.Right, root.Leftreturn root
}

/*** Definition for a binary tree node.* type TreeNode struct {*     Val int*     Left *TreeNode*     Right *TreeNode* }*/
func invertTree(root *TreeNode) *TreeNode {// 基礎情況：如果當前節點為空，直接返回// 這是遞歸的終止條件，空節點不需要翻轉if root == nil {return root}// 遞歸地翻轉左子樹// 將左子樹完全翻轉后，返回翻轉后的左子樹根節點root.Left = invertTree(root.Left)// 遞歸地翻轉右子樹// 將右子樹完全翻轉后，返回翻轉后的右子樹根節點root.Right = invertTree(root.Right)// 交換當前節點的左右子節點// 使用Go的多重賦值特性，不需要臨時變量root.Left, root.Right = root.Right, root.Left// 返回翻轉后的當前子樹根節點return root
}

101. 對稱二叉樹

題目

給你一個二叉樹的根節點 root ， 檢查它是否軸對稱。

示例 1：

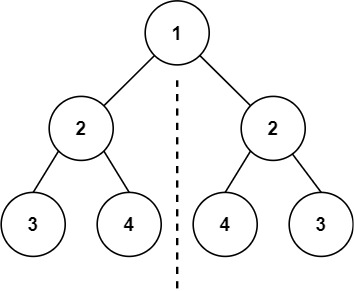
輸入：root = [1,2,2,3,4,4,3]
輸出：true

示例 2：

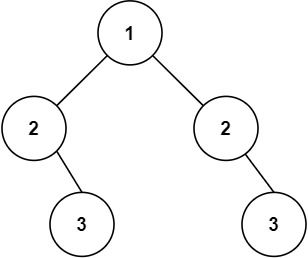
輸入：root = [1,2,2,null,3,null,3]
輸出：false

提示：

樹中節點數目在范圍 [1, 1000] 內
-100 <= Node.val <= 100

進階：你可以運用遞歸和迭代兩種方法解決這個問題嗎？

總體思路

這段代碼使用**廣度優先搜索（BFS）**的方法來判斷二叉樹是否軸對稱（鏡像對稱）。其核心思想是：

1. 將需要比較的節點成對放入隊列中（左子樹的左節點 vs 右子樹的右節點，左子樹的右節點 vs 右子樹的左節點）
2. 每次從隊列中取出一對節點進行比較
3. 如果所有對應的節點對都滿足鏡像關系，則二叉樹是對稱的

時間復雜度與空間復雜度

時間復雜度：O(n)

• 每個節點最多被訪問一次，n為二叉樹中的節點數量
• 每個節點進行常數時間的比較操作

空間復雜度：O(n)

• 在最壞情況下（完全二叉樹），隊列中最多會存儲約n/2個節點對
• 空間復雜度主要由隊列的大小決定

代碼

golang

/*** Definition for a binary tree node.* type TreeNode struct {*     Val int*     Left *TreeNode*     Right *TreeNode* }*/
func isSymmetric(root *TreeNode) bool {if root == nil {return true}type pair struct{l, r *TreeNode}q := []pair{{root.Left, root.Right}}for len(q) > 0 {p := q[0]q = q[1:]left, right := p.l, p.rif left == nil && right == nil {continue}if left == nil || right == nil {return false}if left.Val != right.Val {return false}q = append(q,pair{left.Left,right.Right})q = append(q, pair{left.Right, right.Left})}return true
}

package maintype TreeNode struct {Val   intLeft  *TreeNodeRight *TreeNode
}// isSymmetric 判斷二叉樹是否軸對稱（鏡像對稱）
func isSymmetric(root *TreeNode) bool {// 如果根節點為空，空樹被認為是對稱的if root == nil {return true}// 定義pair結構體來存儲需要比較的一對節點// l: 左子樹中的某個節點，r: 右子樹中對應的鏡像節點type pair struct{ l, r *TreeNode }// 初始化隊列，首先將根節點的左右子節點作為第一對需要比較的節點q := []pair{{root.Left, root.Right}}// 當隊列不為空時循環處理for len(q) >  {// 從隊列頭部取出一對節點p := q[0]q = q[1:]  // 移除隊列頭部元素left, right := p.l, p.r// 如果兩個節點都為空，說明對稱，繼續檢查其他節點對if left == nil && right == nil {continue}// 如果只有一個節點為空，另一個不為空，說明不對稱if left == nil || right == nil {return false}// 如果兩個節點都不為空，但值不相等，說明不對稱if left.Val != right.Val {return false}// 將下一層需要比較的節點對加入隊列：// 1. 左節點的左子節點 vs 右節點的右子節點（外側比較）// 2. 左節點的右子節點 vs 右節點的左子節點（內側比較）q = append(q, pair{left.Left, right.Right})q = append(q, pair{left.Right, right.Left})}// 如果所有節點對都通過檢查，說明二叉樹是對稱的return true
}

知識點

q := []pair{{root.Left, root.Right}}

這一行是 Go 語言里“構造切片并初始化第一個元素”的寫法，拆開來看就明白了：

1. []pair{ ... }
   表示創建一個元素類型為 pair 的切片（slice）。
2. {{root.Left, root.Right}}
   切片里只放 一個元素，這個元素又是一個 pair 結構體，所以用兩層花括號：
   • 外層 {} 是“切片字面量”；
   • 內層 {} 是“結構體字面量”，給 pair 的字段 l、r 分別賦值為 root.Left 和 root.Right。

等價于：

q := make([]pair, 0, 1)
q = append(q, pair{l: root.Left, r: root.Right})

只是第一種寫法更簡潔，常用來一次性初始化切片。