一、前綴和數組

要稍微注意前綴和數組從1開始

#include <iostream>using namespace std;const int N = 100010;int n, m;
int a[N], s[N];int main()
{scanf("%d%d", &n, &m);for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);for (int i = 1; i <= n; i ++ ) s[i] = s[i - 1] + a[i]; // 前綴和的初始化while (m -- ){int l, r;scanf("%d%d", &l, &r);printf("%d\n", s[r] - s[l - 1]); // 區間和的計算}return 0;
}

二、子矩陣的和

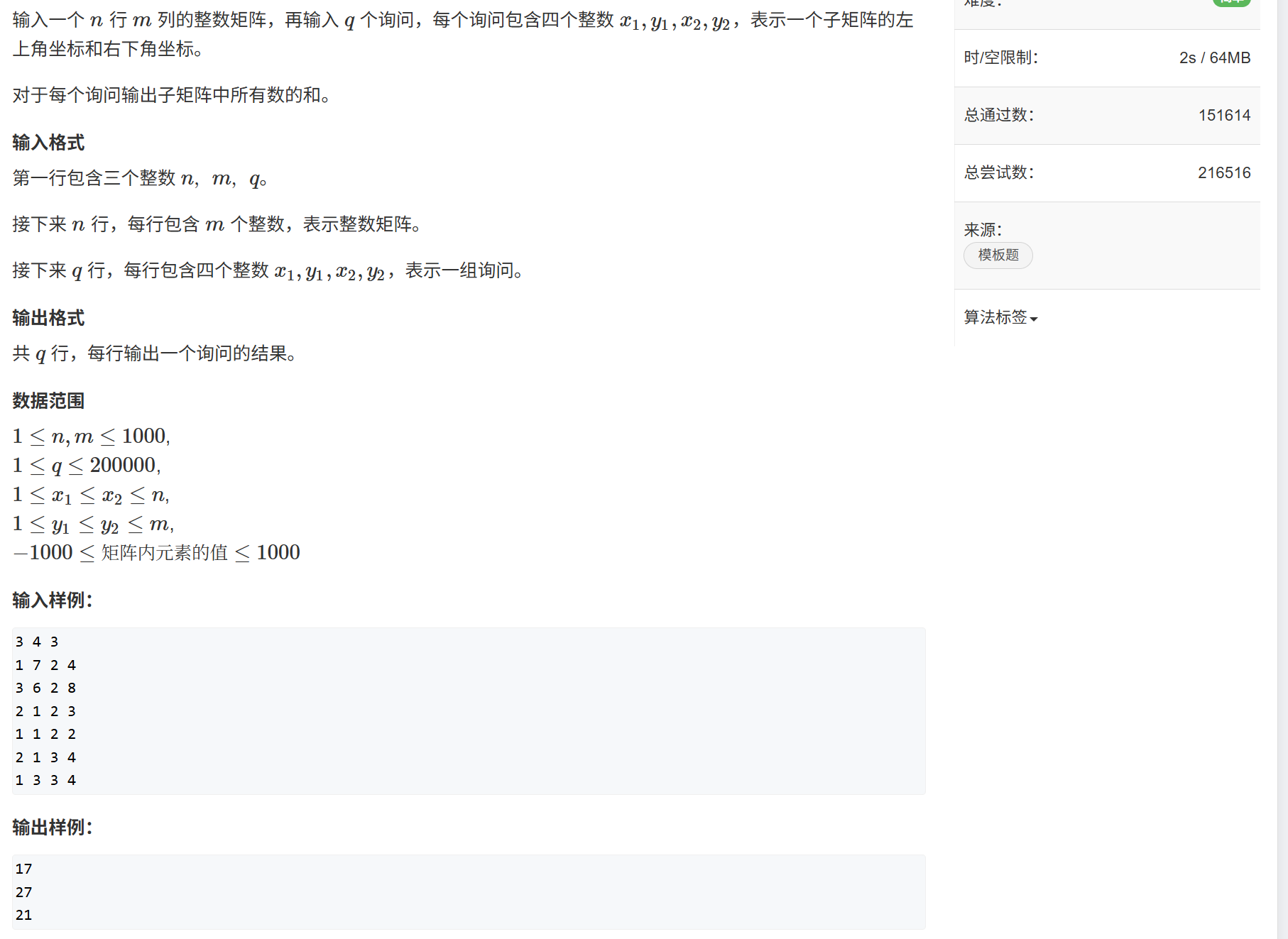
S[i,j]表示本身及其左上部分矩陣所有元素的和，再用容斥原理計算某個子矩陣的和

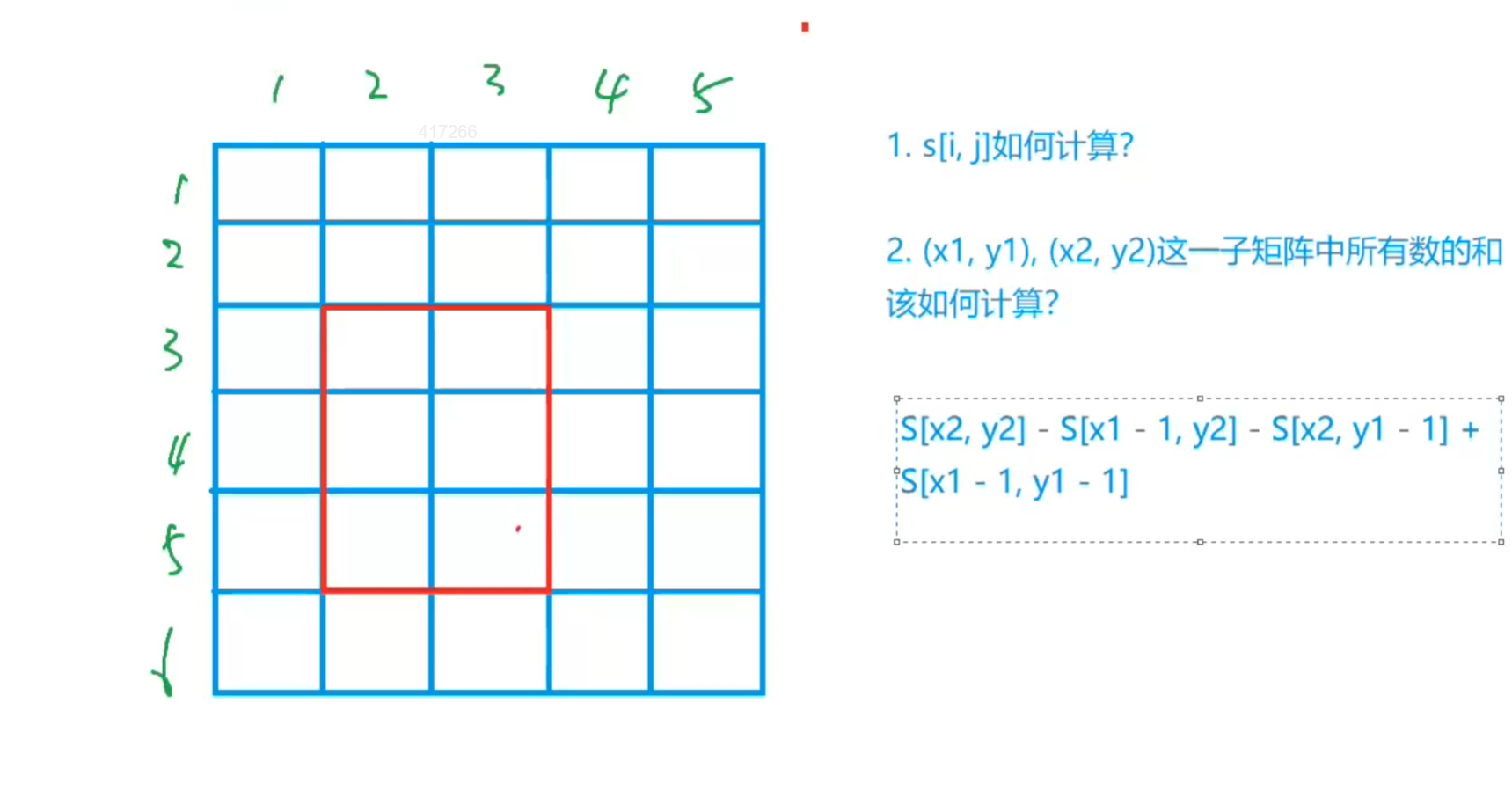
#include <iostream>using namespace std;const int N = 1010;int n, m, q;
int s[N][N];int main()
{scanf("%d%d%d", &n, &m, &q);for (int i = 1; i <= n; i ++ )for (int j = 1; j <= m; j ++ )scanf("%d", &s[i][j]);for (int i = 1; i <= n; i ++ )for (int j = 1; j <= m; j ++ )s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];while (q -- ){int x1, y1, x2, y2;scanf("%d%d%d%d", &x1, &y1, &x2, &y2);printf("%d\n", s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1]);}return 0;
}

三、差分數組

構造b數組，使得a數組是b數組的前綴和即可，對b數組進行O(1)復雜度操作再對b計算一次前綴和即可得到更新后的a數組，b[l]+c,b[r+1]-c

差分的構造即a[i]-a[i-1]

原數組的構造可以看作是對差分數組[i,i]區間的元素加ai

#include <iostream>using namespace std;const int N = 100010;int n, m;
int a[N], b[N];void insert(int l, int r, int c)
{b[l] += c;b[r + 1] -= c;
}int main()
{scanf("%d%d", &n, &m);for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);for (int i = 1; i <= n; i ++ ) insert(i, i, a[i]);while (m -- ){int l, r, c;scanf("%d%d%d", &l, &r, &c);insert(l, r, c);}for (int i = 1; i <= n; i ++ ) b[i] += b[i - 1];for (int i = 1; i <= n; i ++ ) printf("%d ", b[i]);return 0;
}

四、差分矩陣

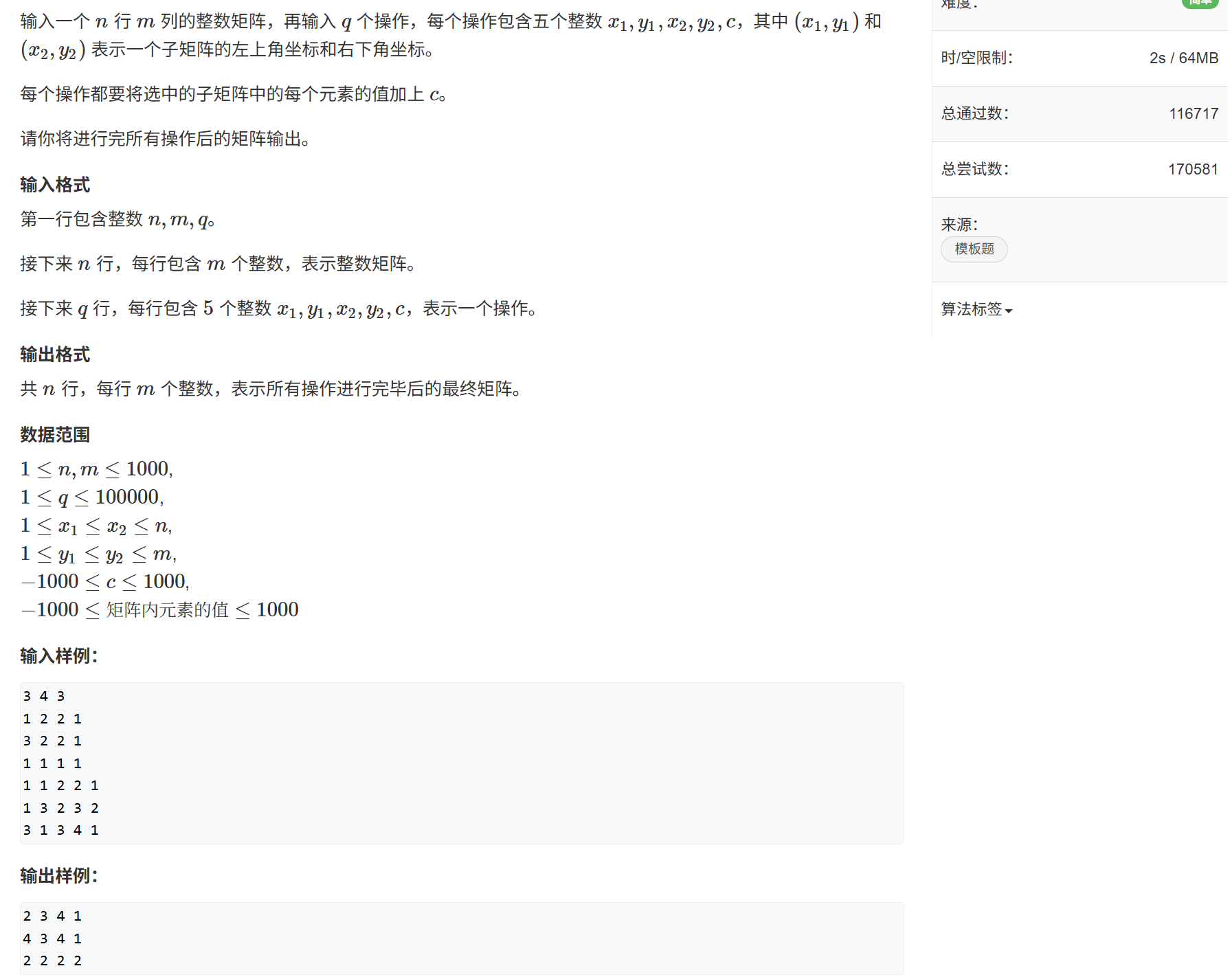
#include <iostream>using namespace std;const int N = 1010;int n, m, q;
int a[N][N], b[N][N];void insert(int x1, int y1, int x2, int y2, int c)
{b[x1][y1] += c;b[x2 + 1][y1] -= c;b[x1][y2 + 1] -= c;b[x2 + 1][y2 + 1] += c;
}int main()
{scanf("%d%d%d", &n, &m, &q);for (int i = 1; i <= n; i ++ )for (int j = 1; j <= m; j ++ )scanf("%d", &a[i][j]);for (int i = 1; i <= n; i ++ )for (int j = 1; j <= m; j ++ )insert(i, j, i, j, a[i][j]);while (q -- ){int x1, y1, x2, y2, c;cin >> x1 >> y1 >> x2 >> y2 >> c;insert(x1, y1, x2, y2, c);}for (int i = 1; i <= n; i ++ )for (int j = 1; j <= m; j ++ )b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];for (int i = 1; i <= n; i ++ ){for (int j = 1; j <= m; j ++ ) printf("%d ", b[i][j]);puts("");}return 0;
}