從機器學習的角度實現 excel 中趨勢線：揭秘梯度下降過程

1. 引言：Excel 的“一鍵魔法”背后藏著什么智慧？

在 Excel 中，我們只需右鍵 → 添加趨勢線，一條完美的直線就出現了。它快得像魔法，但魔法背后，是數學的嚴謹。

今天，我們不關心 Excel 內部用了什么算法（可能是解析法），而是要問：

如果機器一開始‘什么都不知道’，它該怎么一步步‘學會’畫出這條線？

2. 我們的任務：預測一個簡單的線性關系

假設我們有一組數據，它們大致遵循 y = 2x + 1 的規律，但有一些隨機噪聲（模擬真實世界的測量誤差）。

我們的目標：僅憑這10個數據點，讓機器“學會”這個規律，找到最佳的 a（斜率）和 b（截距）。

3. 準備數據：10 個“玩具”樣本

我們用 Python 生成這10個數據點：

import numpy as np
import matplotlib.pyplot as plt# 設置隨機種子，保證結果可復現
np.random.seed(42)# 生成 10 個 x 值，從 1 到 10
x = np.arange(1, 11)  # [1, 2, 3, ..., 10]# 生成 y 值：y = 2x + 1 + 噪聲
true_a, true_b = 2, 1
noise = np.random.normal(0, 0.5, size=x.shape)  # 添加標準差為 0.5 的高斯噪聲
y = true_a * x + true_b + noise# 查看數據
print("x:", x)
print("y:", np.round(y, 2))  # 保留兩位小數

輸出：

x: [ 1  2  3  4  5  6  7  8  9 10]
y: [ 3.25  4.93  7.32  9.76 10.88 12.88 15.79 17.38 18.77 21.27]

關鍵點：真實規律是 y = 2x + 1，但數據有噪聲，所以 y 值不完全精確。

4. 可視化：我們的目標是什么？

讓我們畫出這些數據點，并標出真實的線（y=2x+1）：

plt.figure(figsize=(8, 6))
plt.scatter(x, y, color='blue', label='真實數據點', s=50)
# 畫出真實規律的線
x_line = np.linspace(0, 11, 100)
y_line = true_a * x_line + true_b
plt.plot(x_line, y_line, 'g--', label=f'真實規律 y={true_a}x+{true_b}', linewidth=2)plt.xlabel('x')
plt.ylabel('y')
plt.title('我們的“學習”任務：根據10個數據點，找到最佳擬合線')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()

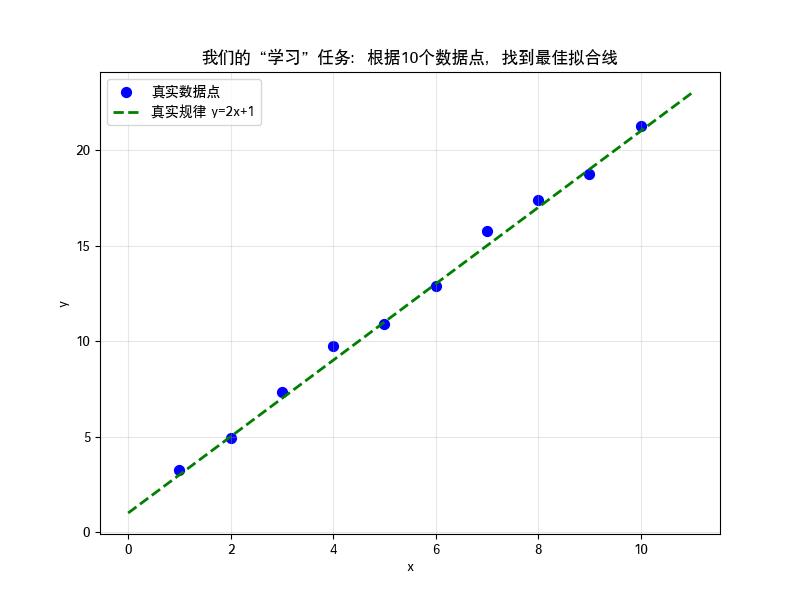
我們的任務就是：僅從這些藍色散點，讓機器找到一條最接近綠色虛線的直線。

**5. 模型定義：`y_pred = a * x + b`**

我們假設模型的形式是：

y_pred = a * x + b

a：斜率（slope）
b：截距（intercept）
初始時，我們不知道?a?和?b?是多少，可以先猜一個值，比如?a=0, b=0。

6. 損失函數：我們“錯”了多少？

我們需要一個“尺子”來衡量預測的好壞。用均方誤差 (MSE)：

MSE = (1/n) * Σ(y - y_pred)2

代碼實現：

def compute_mse(y_true, y_pred):return np.mean((y_true - y_pred) ** 2)# 初始猜測：a=0, b=0
a, b = 0.0, 0.0
y_pred_initial = a * x + b
initial_loss = compute_mse(y, y_pred_initial)
print(f"初始損失 (a=0, b=0): {initial_loss:.3f}")

初始損失 (a=0, b=0): 182.431

解釋：損失很大，因為 y_pred 全是 0，和真實 y 差很遠。

7. 核心：梯度下降——如何“學習”？

現在，我們教模型如何“學習”：

比喻：你在濃霧中的山坡上，想找到谷底（損失最小的地方）。你看不見路，但能感覺到腳下的坡度（梯度）。你每次都向坡度最陡的下坡方向走一步（更新參數），一步步接近谷底。
數學計算（對 a 和 b 求偏導）：
- ?MSE/?a = (2/n) * Σ((a*x + b - y) * x)
- ?MSE/?b = (2/n) * Σ(a*x + b - y)
更新規則：
- a = a - learning_rate * ?MSE/?a
- b = b - learning_rate * ?MSE/?b

8. 動手實現：手動訓練模型

# 超參數
learning_rate = 0.01  # 學習率，步長
epochs = 10000           # 訓練輪數# 初始化參數
a, b = 0.0, 0.0# 記錄歷史，用于畫圖
loss_history = []
a_history = []
b_history = []for i in range(epochs):# 前向：計算預測值y_pred = a * x + b# 計算損失loss = compute_mse(y, y_pred)loss_history.append(loss)a_history.append(a)b_history.append(b)# 計算梯度n = len(x)da = (2 / n) * np.sum((y_pred - y) * x)  # 注意：y_pred - ydb = (2 / n) * np.sum(y_pred - y)# 更新參數a = a - learning_rate * dab = b - learning_rate * db# 打印進度if (i+1) % 1000 == 0:print(f"第 {i+1} 輪: a={a:.3f}, b={b:.3f}, 損失={loss:.3f}")print(f"\n訓練完成！")
print(f"我們的模型找到: a ≈ {a:.3f}, b ≈ {b:.3f}")
print(f"真實規律是: a = {true_a}, b = {true_b}")

輸出：

第 100 輪: a=2.054, b=0.840, 損失=0.153
第 200 輪: a=2.021, b=1.070, 損失=0.124
第 300 輪: a=2.007, b=1.168, 損失=0.119
第 400 輪: a=2.001, b=1.211, 損失=0.118
第 500 輪: a=1.999, b=1.229, 損失=0.118
第 600 輪: a=1.997, b=1.237, 損失=0.118
第 700 輪: a=1.997, b=1.240, 損失=0.118
第 800 輪: a=1.997, b=1.242, 損失=0.118
第 900 輪: a=1.997, b=1.243, 損失=0.118
第 1000 輪: a=1.997, b=1.243, 損失=0.118訓練完成！
我們的模型找到: a ≈ 1.997, b ≈ 1.243
真實規律是: a = 2, b = 1

看！模型通過1000次迭代，a 從 0 逐漸接近 2，b 接近 1，損失不斷下降。

9. 可視化學習過程

損失下降曲線：

plt.plot(loss_history)
plt.xlabel('訓練輪數 (Epoch)')
plt.ylabel('損失 (MSE)')
plt.title('損失隨訓練過程下降')
plt.grid(True, alpha=0.3)
plt.show()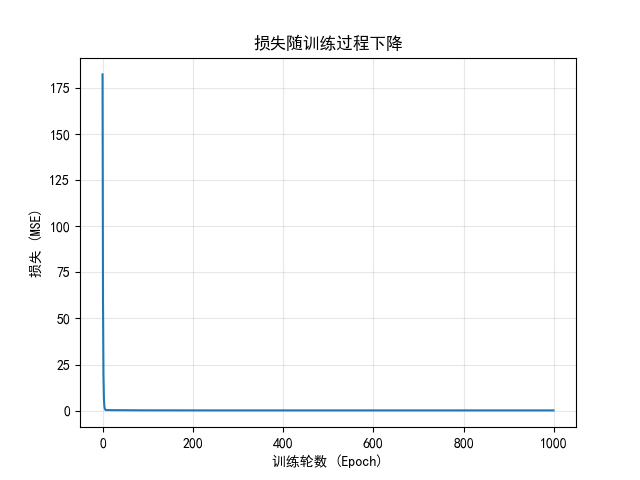

參數變化過程：

plt.plot(a_history, label='a (斜率)')
plt.plot(b_history, label='b (截距)')
plt.axhline(y=true_a, color='g', linestyle='--', label='真實 a')
plt.axhline(y=true_b, color='r', linestyle='--', label='真實 b')
plt.xlabel('訓練輪數')
plt.ylabel('參數值')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()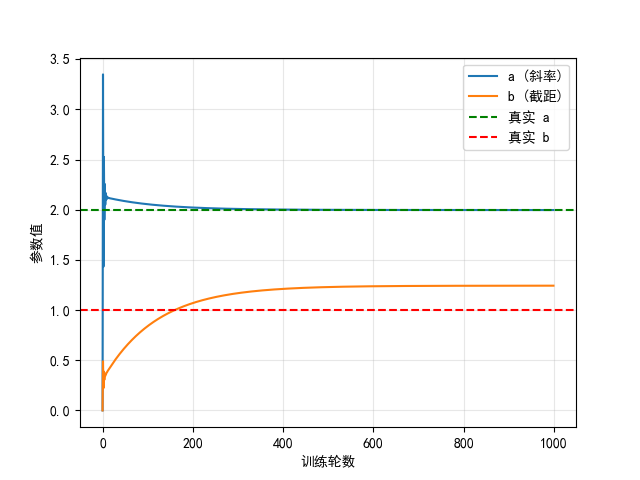

最終擬合結果：

plt.figure(figsize=(8, 6))
plt.scatter(x, y, color='blue', label='真實數據點', s=50)
plt.plot(x_line, y_line, 'g--', label=f'真實規律 y={true_a}x+{true_b}', linewidth=2)
plt.plot(x_line, a * x_line + b, 'r-', label=f'擬合線 y={a:.2f}x+{b:.2f}', linewidth=2)
plt.xlabel('x')
plt.ylabel('y')
plt.title('梯度下降擬合結果')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()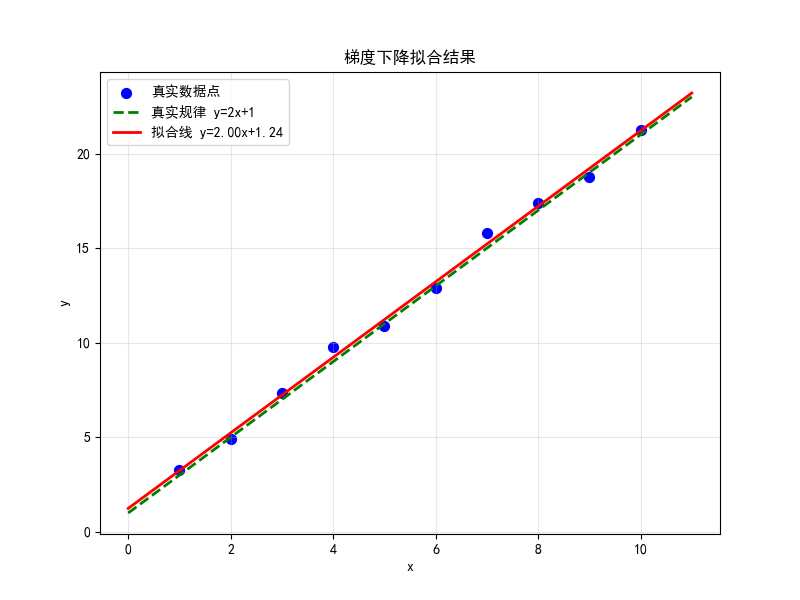

excel擬合結果：

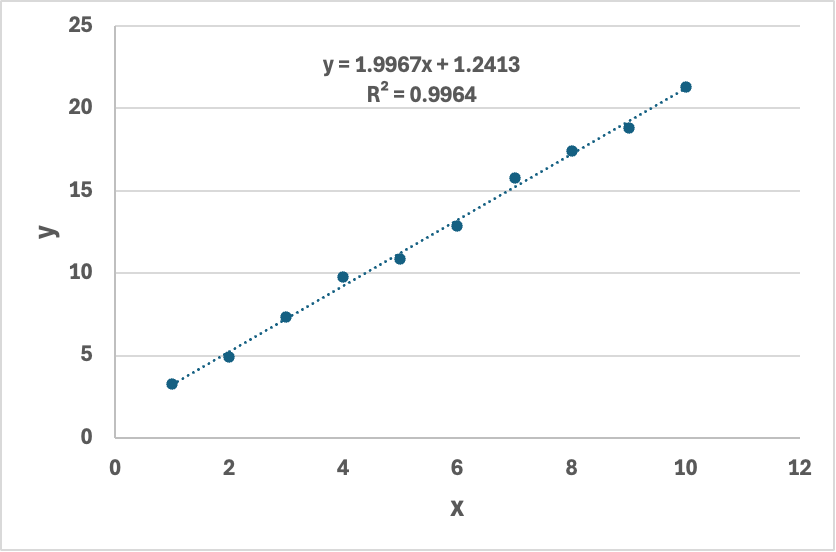
10. 對比專業工具：Scikit-learn

讓我們看看專業的機器學習庫 scikit-learn 是怎么做的：

from sklearn.linear_model import LinearRegression# 注意：sklearn 需要 2D 輸入
X = x.reshape(-1, 1)model = LinearRegression()
model.fit(X, y)print(f"Scikit-learn 結果: 斜率 a = {model.coef_[0]:.3f}, 截距 b = {model.intercept_:.3f}")

輸出：

Scikit-learn 結果: 斜率 a = 1.997, 截距 b = 1.243

完全一致！ 我們手動實現的梯度下降，和 sklearn 的結果一樣。

附. 深入理解：梯度下降 vs 解析法——殊途同歸的兩種智慧

你可能會問：“我們手動實現的梯度下降，和 scikit-learn 的 LinearRegression，是同一種方法嗎？”

答案是：不是。 它們在求解方式、數學基礎和適用場景上有本質區別。但最終結果一致，是因為它們都在尋找同一個“最優解”。

下面，我們來揭開這個“黑箱”。

一、核心原理：迭代逼近 vs 數學解析

方法	核心思想	求解方式
手動梯度下降	逐步“試錯”，像盲人下山，一步步逼近最優解。	迭代法：重復“計算梯度 → 更新參數”直到收斂。
scikit-learn LinearRegression	直接用數學公式算出理論最優解，一步到位。	解析法（閉式解）：通過公式?`w = (X?X)?1X?y`?直接計算。

1. 手動梯度下降（迭代法）

數學邏輯：
- 定義損失函數（MSE）： $L(a,b) = \frac{1}{n} \sum_{i=1}^{n} (y_i - (ax_i + b))^2$
- 計算梯度（偏導數）： $\frac{\partial L}{\partial a} = \frac{2}{n} \sum_{i=1}^{n} (ax_i + b - y_i) x_i$ ， $\frac{\partial L}{\partial b} = \frac{2}{n} \sum_{i=1}^{n} (ax_i + b - y_i)$
- 更新參數： $a = a - \eta \cdot \frac{\partial L}{\partial a}, \quad b = b - \eta \cdot \frac{\partial L}{\partial b}$ ? ? ?（η?為學習率）
特點：
- 近似解：需要足夠迭代才能接近最優。
- 適用于大數據：可分批處理（如隨機梯度下降）。
- 需調參：學習率、迭代次數等。

2. scikit-learn LinearRegression（解析法）

數學邏輯：
- 將問題表示為矩陣形式： $\mathbf{y} = \mathbf{X}\mathbf{w} + \boldsymbol{\epsilon}$
- 最優參數?ww?的閉式解為： $\mathbf{w} = (\mathbf{X}^T \mathbf{X})^{-1} \mathbf{X}^T \mathbf{y}$
  這個公式是通過對損失函數求導并令其為 0 推導出的理論最優解。
特點：
- 精確解：無需迭代，一步到位。
- 計算復雜度高：矩陣求逆的復雜度為?O(n3)O(n3)，特征數多時很慢。
- 無超參數：直接計算，無需調學習率。

二、關鍵差異對比

維度	梯度下降（迭代法）	LinearRegression（解析法）
求解方式	逐步迭代逼近	直接公式計算
結果性質	近似解（可無限接近）	理論最優解
計算效率	大數據更高效	特征多時慢
超參數依賴	需調學習率、迭代次數	無超參數
適用場景	大數據、高維（如深度學習）	小數據、低維（如本例）
數值穩定性	受學習率影響	受多重共線性影響