LeetCode算法日記 - Day 29: 重排鏈表、合并 K 個升序鏈表

1. 重排鏈表

1.1 題目解析

1.2 解法

1.3 代碼實現

2. 合并 K 個升序鏈表

2.1 題目解析

2.2 解法

2.3 代碼實現

1. 重排鏈表

143. 重排鏈表 - 力扣（LeetCode）

給定一個單鏈表?L?的頭節點?head?，單鏈表?L?表示為：

L0 → L1 → … → Ln - 1 → Ln

請將其重新排列后變為：

L0 → Ln → L1 → Ln - 1 → L2 → Ln - 2 → …

不能只是單純的改變節點內部的值，而是需要實際的進行節點交換。

示例 1：

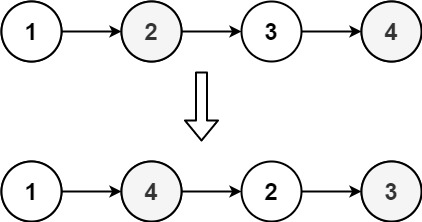
輸入：head = [1,2,3,4]
輸出：[1,4,2,3]

示例 2：

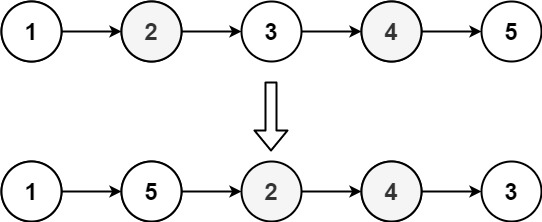
輸入：head = [1,2,3,4,5]
輸出：[1,5,2,4,3]

提示：

鏈表的長度范圍為?[1, 5 * 104]
1 <= node.val <= 1000

1.1 題目解析

題目本質
把鏈表“重排”為首尾交替：L0, L1, …, Ln → L0, Ln, L1, Ln-1, …。本質是按位置重新連接指針，不能改節點值、不能新建整條鏈，只能原地改 .next。

常規解法
最直觀：把所有節點放進數組，然后雙指針從兩端往中間，按順序重連。

問題分析
數組法需要 O(n) 額外空間，不滿足“盡量原地”的典型考點；且頻繁重連要小心斷鏈與成環。期望是 O(1) 額外空間、O(n) 時間 的指針操作。

思路轉折
要首尾交替，其實就是：
1）找到中點，把鏈表一分為二；
2）反轉后半段，使其順序變為 Ln, Ln-1, …；
3）交替合并前半（L0, L1, …）和反轉后的后半（Ln, …）。
這樣天然實現“首尾交替”。中點建議取左中點（（while (fast.next != null && fast.next.next != null)），保證后半長度 ≤ 前半，合并時只需“把后半用盡”為止，循環條件寫 while (p2 != null) 最穩。

1.2 解法

算法思想
設鏈表為 head：

慢快指針找左中點 slow；
斷開：second = slow.next; slow.next = null；
反轉 second 得 revSecond；

兩指針 p1 = head, p2 = revSecond，交替接：

n1 = p1.next; n2 = p2.next;
p1.next = p2; p2.next = n1;
p1 = n1; p2 = n2;

當 p2 用盡，結束（奇數長度時前半多一個尾結點，正好留在末尾）。

i）左中點：while (fast.next != null && fast.next.next != null) { slow=slow.next; fast=fast.next.next; }

ii）斷開：second = slow.next; slow.next = null;

iii）反轉后半：三指針 prev/curr/next 原地反轉，返回新頭 prev。

iiii）交替合并：每輪先保存 n1 = p1.next, n2 = p2.next，再改指針，最后推進到 n1/n2。

iiiii）結束：函數為 void，就地修改，無需返回。

易錯點

早退條件：if (head == null || head.next == null) return;（不是 &&）。
快慢指針寫法：為得到左中點，條件用 fast.next != null && fast.next.next != null。
斷開前半尾：slow.next = null; 必須斷開，否則可能成環。
反轉必須先存 next：next：next = curr.next; 之后再改 curr.next = prev，否則斷路找不到后繼。
合并時別用錯指針：保存/連接用 p1/p2 的 next，不是 head/second 的 next。
循環條件：while (p2 != null)，因為后半長度 ≤ 前半，合并完后半即完成。
不創建新節點：只能改 .next，不能重新 new 組成整條鏈。

1.3 代碼實現

/*** Definition for singly-linked list.* public class ListNode {*     int val;*     ListNode next;*     ListNode() {}*     ListNode(int val) { this.val = val; }*     ListNode(int val, ListNode next) { this.val = val; this.next = next; }* }*/
class Solution {public void reorderList(ListNode head) {// 0) 早退：空鏈或單節點，無需處理if (head == null || head.next == null) return;// 1) 快慢指針找“左中點” slowListNode slow = head, fast = head;while (fast.next != null && fast.next.next != null) {slow = slow.next;fast = fast.next.next;}// 2) 斷開并反轉后半段ListNode second = slow.next;slow.next = null;                 // 斷開前半尾second = reverse(second);         // 原地反轉后半// 3) 交替合并：前半(head)與后半(second, 已反轉)ListNode p1 = head, p2 = second;while (p2 != null) {ListNode n1 = p1.next, n2 = p2.next; // 先保存后繼，避免斷路p1.next = p2;p2.next = n1;p1 = n1;p2 = n2;}// 就地修改，void 無需返回}// 三指針原地反轉private ListNode reverse(ListNode head) {ListNode prev = null, curr = head;while (curr != null) {ListNode next = curr.next; // 保存舊路口curr.next = prev;          // 反轉指向prev = curr;               // prev 前進curr = next;               // curr 走向舊路口}return prev; // 新頭}
}

復雜度分析

時間復雜度：O(n)（找中點 O(n/2) + 反轉 O(n/2) + 合并 O(n)）。
空間復雜度：O(1)（只用常數級指針變量，原地修改）。

2. 合并 K 個升序鏈表

23. 合并 K 個升序鏈表 - 力扣（LeetCode）

給你一個鏈表數組，每個鏈表都已經按升序排列。

請你將所有鏈表合并到一個升序鏈表中，返回合并后的鏈表

示例 1：

輸入：lists = [[1,4,5],[1,3,4],[2,6]]
輸出：[1,1,2,3,4,4,5,6]
解釋：鏈表數組如下：
[1->4->5,1->3->4,2->6
]
將它們合并到一個有序鏈表中得到。
1->1->2->3->4->4->5->6

示例 2：

輸入：lists = []
輸出：[]

示例 3：

輸入：lists = [[]]
輸出：[]

提示：

k == lists.length
0 <= k <= 10^4
0 <= lists[i].length <= 500
-10^4 <= lists[i][j] <= 10^4
lists[i]?按?升序?排列
lists[i].length?的總和不超過?10^4

2.1 題目解析

題目本質
把 k 條已升序的鏈表合成 1 條升序鏈表。抽象成：從 k 個“有序流”的當前表頭中，持續選出最小元素并接到結果尾部，直到所有流耗盡。

常規解法
每一步在 k 個表頭里線性找最小，接到結果鏈表尾部。

問題分析
線性掃描每步 O(k)，總共有 N 次選擇（N 為所有節點總數），總時間 O(N·k)。當 k 很大（最多 10^4）時會明顯超時。

思路轉折
要把“每步找最小”從 O(k) 降到 O(log k)：

路線 A：小根堆裝 k 個表頭，poll/offer 均 O(log k)，整體 O(N log k)。
路線 B：分治兩兩合并（像歸并排序）：每層線性合并，總層數 log k，整體 O(N log k)。
建議：
代碼短、直觀：小根堆。
不想引入堆、掌握分治：兩兩合并。

2.2 解法

2.2.1 分治兩兩合并
把區間 [0..k-1] 的鏈表遞歸二分為 [l..m] 和 [m+1..r]，分別合并成兩條有序鏈，再調用“合并兩條有序鏈表”得到當前區間的答案。
遞推：mergeRange(l,r) = mergeTwo( mergeRange(l,m), mergeRange(m+1,r) )。

i）邊界：lists?== null或lists.length == 0?返回 null；l==r 返回 lists[l]（可為 null）。

ii）遞歸：中點 m = l + (r-l)/2，分別合并左右。

iii）合并兩條鏈：用局部 dummy 與 tail，每次接更小的那個節點；某一條耗盡后把另一條一次性掛尾。

易錯點

dummy/tail 必須是合并函數的局部變量，不要復用全局，否則容易把不同子問題的結果“接成環”，遍歷超時。
合并時推進順序：tail.next = a/b → 移動 a/b = a/b.next → tail = tail.next。
收尾：不要循環一個個接剩余部分，直接 tail.next = (a!=null ? a : b)。
輸入可能包含空鏈：初始化和遞歸都要兼容 null。

2.2.2 小根堆
維護一個小根堆保存“每條鏈當前表頭”，每次彈出最小節點接入結果；若該節點有 next，把 next 放回

易錯點

Java 用 PriorityQueue<ListNode>，比較器使用 Integer.compare(a.val, b.val)，避免 b - a 溢出。
只把表頭入堆，而不是把整條鏈全部入堆。

2.3 代碼實現

方案一：分治兩兩合并

/*** Definition for singly-linked list.* public class ListNode {*     int val;*     ListNode next;*     ListNode() {}*     ListNode(int val) { this.val = val; }*     ListNode(int val, ListNode next) { this.val = val; this.next = next; }* }*/
class Solution {public ListNode mergeKLists(ListNode[] lists) {if (lists == null || lists.length == 0) return null;return mergeRange(lists, 0, lists.length - 1);}private ListNode mergeRange(ListNode[] lists, int l, int r) {if (l == r) return lists[l];                 // 可能為 null，無妨int m = l + (r - l) / 2;ListNode a = mergeRange(lists, l, m);ListNode b = mergeRange(lists, m + 1, r);return mergeTwo(a, b);}private ListNode mergeTwo(ListNode a, ListNode b) {ListNode dummy = new ListNode(0);ListNode tail  = dummy;while (a != null && b != null) {if (a.val <= b.val) {tail.next = a; a = a.next;} else {tail.next = b; b = b.next;}tail = tail.next;}tail.next = (a != null) ? a : b;             // 一次性掛尾return dummy.next;}
}

復雜度分析

時間：O(N log k)（每層線性合并，總層數約 log k）。
空間：O(log k)（遞歸棧；若考慮輸出鏈表為必需空間則不計入額外空間）。

方案二：小根堆

import java.util.PriorityQueue;class Solution {public ListNode mergeKLists(ListNode[] lists) {if (lists == null || lists.length == 0) return null;PriorityQueue<ListNode> pq = new PriorityQueue<>((x, y) -> Integer.compare(x.val, y.val));for (ListNode h : lists) if (h != null) pq.offer(h);ListNode dummy = new ListNode(0), tail = dummy;while (!pq.isEmpty()) {ListNode node = pq.poll();tail.next = node; tail = node;if (node.next != null) pq.offer(node.next);}return dummy.next;}
}

復雜度分析