【智能化解決方案】大模型智能推薦選型系統方案設計

大模型智能推薦選型系統方案設計

- 0 背景
- 1 問題分析與定義
- 2 模型假設與簡化
- 3 核心模型構建
- - 3.1 決策變量與參數定義
  - 3.2 目標函數
  - 3.3 約束條件
- 4 模型求解與驗證
- - 4.1 求解策略
  - 4.2 驗證方法
  - 4.3 模型迭代優化
- 5 方案實施與系統設計
- - 5.1 系統架構設計
  - 5.2 工作流程
  - 5.3 關鍵算法實現
  - 5.4 時序圖
  - 5.5 應用示例
- 6 使用實例
- 7 總結與展望

0 背景

現有的模型選型設計過程存在以下缺陷：
（1）場景適配僵化： 現有組合策略依賴人工經驗固化流程，無法動態響應業務需求變化。
（2）評估體系割裂： 模型效果/成本/合規性評估分散在不同系統（MLFlow僅跟蹤性能，Prometheus監控資源，模型評估工具分析效果），缺乏統一量化標準，難以衡量是否是最終最優解，易造成設計方案的缺陷。
（3）可解釋性較差： 傳統符號邏輯、智能推薦算法的可解釋性較差，對決策過程、設計依據缺少詳盡的分析決策過程。
（4）人工設計難度高： 針對傳統的多模型動態協同策略設計，對設計者要求較高，需要有較強的需求分析能力，并且了解模型的性能、成本、效果等指標，設計周期平均超過3工作日，效率較低。

故希望設計一套大模型智能推薦選型系統，構建動態響應機制，通過實時分析業務場景特征（復雜度、時延要求、成本閾值），動態生成最優模型組合策略，替代人工固化流程。

1 問題分析與定義

模型搜索推薦問題本質上是一個多目標優化問題，需要在眾多模型特征和性能指標間進行權衡，為用戶特定場景找到最優模型或模型組合。根據提供的模型特征指標，我們可以將問題轉化為數學語言：

目標：構建一個推薦系統，基于用戶場景需求（如數學推理、專業問答、代碼生成等）和約束條件（如顯存限制、成本預算、響應時間要求），從模型庫中選擇最優模型或模型組合。

決策變量：定義二值決策變量 $xi∈{0,1}x_i \in \{0,1\}$ ，表示是否選擇模型 $i$ （當選擇時 $x_i = 1$ ，否則為 $0$ ）。

關鍵約束：

功能約束：模型需支持用戶所需的模態和業務類型
資源約束：顯存占用、計算量不超過可用資源
性能約束：響應時間、準確率等指標滿足最低要求
成本約束：推理成本控制在預算范圍內

優化目標：最大化模型綜合能力得分，最小化成本與響應時間，最大化場景能力匹配度。

基于數學建模的標準流程，我們需要將現實問題通過抽象化和模型化轉化為可計算的數學問題。模型搜索推薦問題的核心在于建立需求與能力之間的數學映射關系，并通過優化算法找到最優解。

2 模型假設與簡化

為了降低問題復雜度并使模型可計算，我們引入以下合理假設：

假設1（獨立性假設）：各模型的性能指標可獨立衡量，模型間組合效應可忽略或通過線性加權近似。這使得我們可以將綜合能力分解為各維度得分的加權和。
假設2（線性可加性）：模型在多維度上的綜合表現可以表示為 $Score=∑jwj?sj\text{Score} = \sum_{j} w_j \cdot s_j$ ，其中 $w_j$ 為權重， $s_j$ 為第 $j$ 項能力得分。
假設3（資源可加性）：當多個模型組合部署時，總資源消耗近似等于各模型資源消耗之和，即 $Total_VRAM≈∑ixi?VRAMi\text{Total\_VRAM} \approx \sum_i x_i \cdot \text{VRAM}_i$ 。
假設4（需求可量化）：用戶場景需求可量化為一系列權重向量，如數學推理場景可表示為 $[w_{\text{數學推理}}=0.7, w_{\text{代碼生成}}=0.2, w_{\text{知識百科}}=0.1]$ 。

這些假設雖然簡化了現實情況，但保證了模型在初始階段的可行性和可計算性。隨著系統運行和數據積累，我們可以逐步放松假設，引入更復雜的非線性關系。

3 核心模型構建

3.1 決策變量與參數定義

決策變量：

$xi∈{0,1}x_i \in \{0,1\}$ ：是否選擇模型 $i$ （1表示選擇，0表示不選擇）

參數（以提供的Qwen-1.8B-Chat模型為例說明）：

$s_{ij}$ ：模型 $i$ 在能力 $j$ 上的得分（如數學推理=0.33，代碼生成=0.27等）
$ciinc_i^{\text{in}}$ ：模型 $i$ 的輸入單價（如0.0001元/1k tokens）
$cioutc_i^{\text{out}}$ ：模型 $i$ 的輸出單價（如0.000175元/1k tokens）
$t_i$ ：模型 $i$ 的響應時間（如4.5ms）
$m_i$ ：模型 $i$ 的服務部署顯存（如1GB）
$f_i$ ：模型 $i$ 的綜合推薦得分（如0.565）

用戶需求參數：

$w_j$ ：用戶對能力 $j$ 的重視權重（ $∑jwj=1\sum_j w_j = 1$ ）
$B$ ：用戶預算約束（元/請求）
$TmaxT_{\text{max}}$ ：用戶可接受最大響應時間（ms）
$MmaxM_{\text{max}}$ ：用戶可用最大顯存（GB）

3.2 目標函數

多目標優化函數：

$MaximizeZ=[Z1Z2Z3]=[∑ixi?(∑jwj?sij)?∑ixi?(ciin+ciout)?∑ixi?ti]\text{Maximize} \quad Z = \left[ \begin{array}{c} Z_1 \\ Z_2 \\ Z_3 \end{array} \right] = \left[ \begin{array}{c} \sum_i x_i \cdot (\sum_j w_j \cdot s_{ij}) \\ -\sum_i x_i \cdot (c_i^{\text{in}} + c_i^{\text{out}}) \\ -\sum_i x_i \cdot t_i \end{array} \right]$

其中 $Z_1$ 表示綜合能力得分（最大化）， $Z_2$ 表示總成本（最小化）， $Z_3$ 表示總響應時間（最小化）。

為簡化計算，我們采用加權求和法將多目標轉換為單目標：

$MaximizeZ=α?∑ixi?(∑jwj?sij)Z1??β?∑ixi?(ciin+ciout)Z2??γ?∑ixi?tiZ3?\text{Maximize} \quad Z = \alpha \cdot \frac{\sum_i x_i \cdot (\sum_j w_j \cdot s_{ij})}{Z_1^*} - \beta \cdot \frac{\sum_i x_i \cdot (c_i^{\text{in}} + c_i^{\text{out}})}{Z_2^*} - \gamma \cdot \frac{\sum_i x_i \cdot t_i}{Z_3^*}$

其中 $α,β,γ\alpha, \beta, \gamma$ 為權重系數（ $α+β+γ=1\alpha + \beta + \gamma = 1$ ）， $Z_1^*, Z_2^*, Z_3^*$ 為歸一化因子。

3.3 約束條件

資源約束：
$∑ixi?mi≤Mmax(顯存約束)\sum_i x_i \cdot m_i \leq M_{\text{max}} \quad \text{(顯存約束)}$

性能約束：
$∑ixi?ti≤Tmax(響應時間約束)\sum_i x_i \cdot t_i \leq T_{\text{max}} \quad \text{(響應時間約束)}$

成本約束：
$∑ixi?(ciin+ciout)≤B(成本約束)\sum_i x_i \cdot (c_i^{\text{in}} + c_i^{\text{out}}) \leq B \quad \text{(成本約束)}$

功能約束：
$∑ixi?aik≥Rk,?k∈功能需求集(功能滿足約束)\sum_i x_i \cdot a_{ik} \geq R_k, \quad \forall k \in \text{功能需求集} \quad \text{(功能滿足約束)}$

邏輯約束：
$∑ixi≥1,∑ixi≤Nmax(選擇數量約束)\sum_i x_i \geq 1, \quad \sum_i x_i \leq N_{\text{max}} \quad \text{(選擇數量約束)}$

4 模型求解與驗證

4.1 求解策略

由于該問題本質上是多約束0-1整數規劃問題，屬于NP難問題，我們采用以下求解策略：

預處理：根據硬約束（如功能、顯存）快速過濾不滿足條件的模型，縮小搜索空間
分層求解：先確定最優單模型，再考慮模型組合策略
啟發式算法：采用遺傳算法進行近似最優解搜索，流程如下：

權衡分析：通過帕累托前沿（Pareto Front）展示不同權重下的最優解分布

4.2 驗證方法

為驗證模型有效性，我們采用以下方法：

歷史數據回溯：使用歷史請求數據模擬推薦過程，計算推薦準確率
A/B測試：將模型部署到真實環境，對比新舊方案的關鍵指標
敏感性分析：改變權重參數，觀察推薦結果的穩定性

4.3 模型迭代優化

推薦系統需要持續迭代優化，基于用戶反饋循環改進模型：

$Reward=α?點擊率+β?使用時長+γ?任務完成率\text{Reward} = \alpha \cdot \text{點擊率} + \beta \cdot \text{使用時長} + \gamma \cdot \text{任務完成率}$

通過強化學習框架不斷調整權重參數，使模型更符合用戶真實偏好。

5 方案實施與系統設計

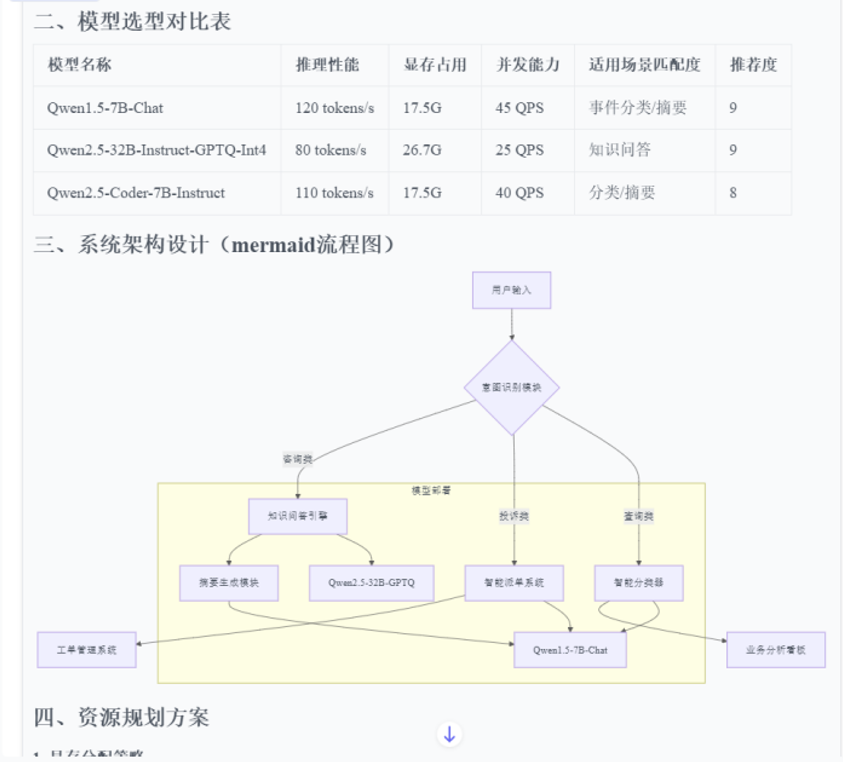
5.1 系統架構設計

基于上述模型，設計一套完整的模型搜索推薦系統，系統架構如下所示：

5.2 工作流程

系統的核心工作流程包括以下步驟：

需求解析：接收用戶原始請求，解析為結構化需求描述
模型過濾：根據硬約束條件快速篩選候選模型集
多目標優化：基于權重配置求解優化問題，得到推薦模型排序
結果生成：生成推薦結果及解釋信息
反饋學習：收集用戶行為數據，優化模型參數

5.3 關鍵算法實現

加權TOPSIS排序算法：

def model_recommendation(user_requirements, models):# 1. 過濾不符合硬約束的模型candidate_models = filter_models(models, user_requirements)# 2. 構建決策矩陣decision_matrix = build_decision_matrix(candidate_models, user_requirements)# 3. 歸一化處理normalized_matrix = normalize_matrix(decision_matrix)# 4. 加權歸一化矩陣weighted_matrix = apply_weights(normalized_matrix, user_requirements['weights'])# 5. 計算理想解與負理想解ideal_best, ideal_worst = calculate_ideal_solutions(weighted_matrix)# 6. 計算相對貼近度similarities = calculate_similarities(weighted_matrix, ideal_best, ideal_worst)# 7. 按貼近度排序并返回return sort_by_similarity(candidate_models, similarities)

5.4 時序圖

系統在處理用戶請求時的內部交互時序如下：

5.5 應用示例

以用戶需要"數學推理"場景為例，演示數學模型的實際應用：

用戶需求：數學推理（權重=0.7），代碼生成（權重=0.2），知識百科（權重=0.1）
約束：顯存≤4GB，響應時間≤1000ms，成本≤0.001元/請求

模型篩選：Qwen-1.8B-Chat符合所有硬約束條件

得分計算：
$Score=0.7×0.33+0.2×0.27+0.1×0.56=0.231+0.054+0.056=0.341\begin{align*} \text{Score} &= 0.7 \times 0.33 + 0.2 \times 0.27 + 0.1 \times 0.56 \\ &= 0.231 + 0.054 + 0.056 = 0.341 \end{align*}$

成本計算：
$Cost=0.0001+0.000175=0.000275元/請求\text{Cost} = 0.0001 + 0.000175 = 0.000275 \text{元/請求}$

綜合評估：
$\times \frac{0.341}{0.5} - 0.2 \times \frac{0.000275}{0.001} - 0.2 \times \frac{4.5}{10} = 0.409 - 0.055 - 0.09 = 0.264$
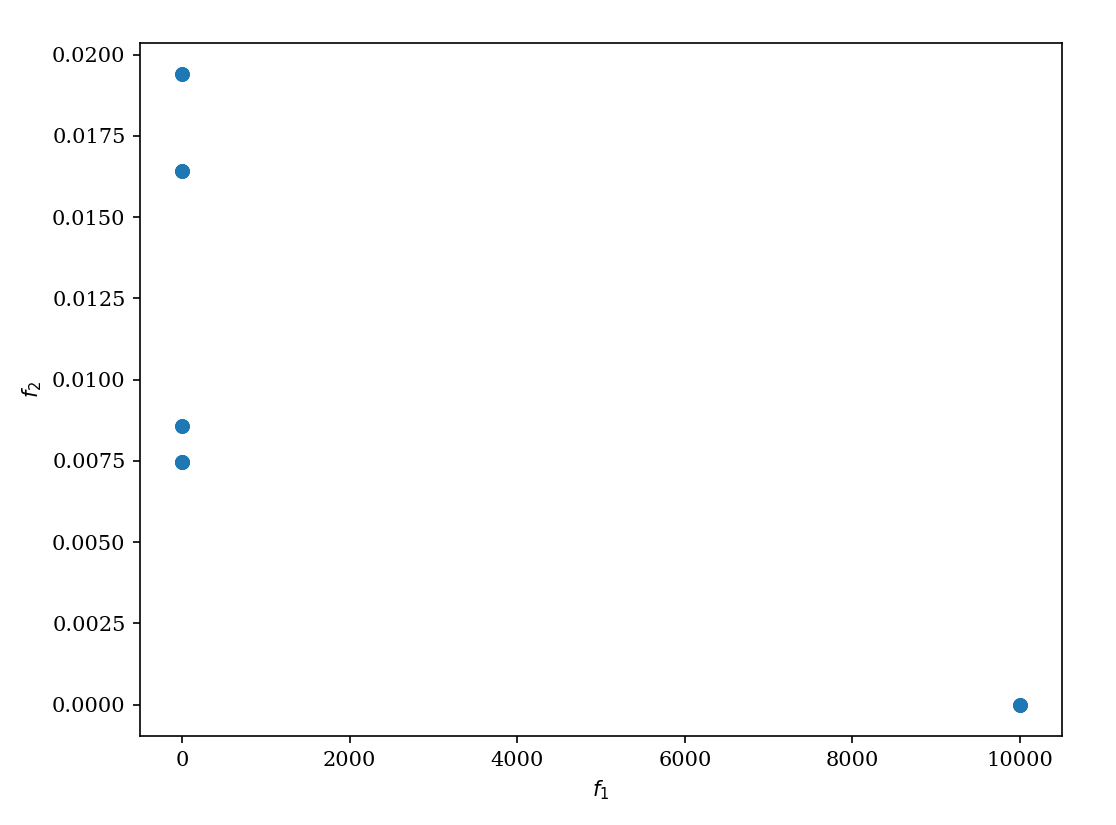
在這里插入圖片描述

通過類似方法計算所有候選模型得分，最終選擇得分最高的模型推薦給用戶。

6 使用實例

在這里插入圖片描述
輸出推薦結果：

為您推薦模型：Qwen1.5-7B-Chat
綜合推薦得分：0.6805 預估成本：0.011000 元/請求所需顯存：60.0 GB
響應時間：1000 ms

推薦理由：

在【數學推理】方面表現優異（得分：0.820，平均水平：0.622）
在【代碼生成pass@1】方面表現優異（得分：0.850，平均水平：0.637）
在【邏輯推理】方面表現優異（得分：0.750，平均水平：0.522）
在【專業問答】方面表現優異（得分：0.670，平均水平：0.423）
在【語義理解】方面表現優異（得分：0.900，平均水平：0.741）
在【生成創作】方面表現優異（得分：0.890，平均水平：0.730）
在【角色扮演】方面表現優異（得分：0.870，平均水平：0.705）
在【安全能力】方面表現優異（得分：0.810，平均水平：0.644）
在【工具使用準確率】方面表現優異（得分：0.820，平均水平：0.624）