一、PCA是什么?
主成分分析(Principal Component Analysis,PCA)是機器學習中最常用的降維技術之一,它通過線性變換將高維數據投影到低維空間,同時保留數據的最重要特征。PCA由卡爾·皮爾遜于1901年發明,如今廣泛應用于數據可視化、特征提取和噪聲過濾等領域。
二、PCA的數學原理
1.1 向量與內積
PCA的核心建立在向量運算基礎上。給定兩個n維向量:
它們的??內積??定義為:
A?B=a1?b1?+a2?b2?+?+an?bn?=∣A∣∣B∣cos(θ)
其中θ是兩向量夾角,|A|表示向量模長:
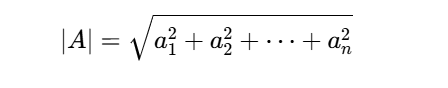
幾何意義??:當|B|=1時,A·B表示A在B方向上的投影長度。
1.2 基與基變換
在n維空間中,??基??是一組線性無關的向量,任何向量都可表示為基的線性組合。標準正交基滿足:
- 每個基向量模長為1
- 任意兩個不同基向量正交(內積為0)
??基變換公式??:設舊基為e1?,e2?,...,en?,新基為p1?,p2?,...,pn?,向量v在新基下的坐標為:
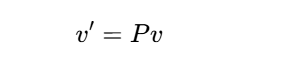
其中P的行向量由新基向量組成。
2.1 優化目標
給定m個n維數據點X=[x1?,x2?,...,xm?],PCA尋找k維(k<n)子空間,使得:
1.?最大方差準則??:投影后數據方差最大化
? ? ? ? ? ? ??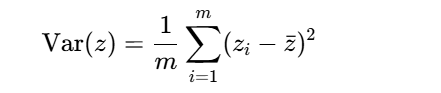
2.最小重構誤差??:重構數據與原數據誤差最小化
? ? ? ? ? ? ? ? ? ? ? ??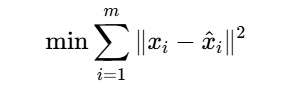
這兩個目標實際上是等價的。
2.2 協方差矩陣
數據經過中心化處理后(均值為0),協方差矩陣為:
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?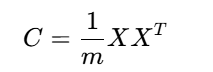
其元素Cij?表示第i維和第j維特征的協方差:
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??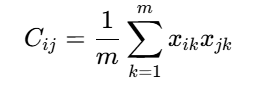
2.3 特征值分解
PCA的關鍵是對協方差矩陣C進行特征值分解:
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??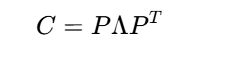
其中:
- ?
Λ是對角矩陣,對角元素λ? ≥ λ? ≥ ... ≥ λ?為特征值
- ?
P的列向量是對應的特征向量,構成新的正交基
??方差解釋??:第i個主成分的方差等于λ?,總方差為∑i=1n?λi?
2.4 降維過程
選擇前k個最大特征值對應的特征向量組成投影矩陣Pk?,降維數據:
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?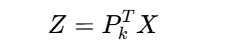
重構數據:
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??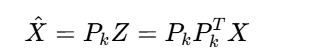
3. PCA算法步驟
3.1 理論步驟
- 數據標準化??:每維特征減去均值
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??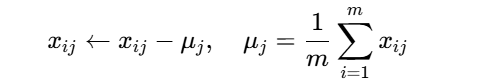
2.計算協方差矩陣??:
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?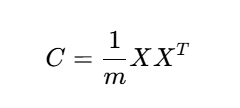
3.特征值分解??:
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??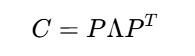
4.??選擇主成分??:按特征值從大到小排序,選擇前k個
5.??數據投影??:
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??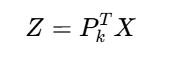
3.2 數值穩定性考慮
實際計算中,常使用??奇異值分解(SVD)??代替特征值分解:
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??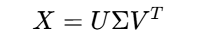
此時:
右奇異矩陣V的列向量即為主成分方向
奇異值σ?與特征值關系:λi?=σi2?/m
三、PCA代碼
1. PCA的Python實現
1.1 數據準備
import numpy as np
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt# 加載鳶尾花數據集
iris = load_iris()
X = iris.data
y = iris.target# 數據標準化
X_centered = X - X.mean(axis=0)1.2 使用scikit-learn實現PCA
from sklearn.decomposition import PCApca = PCA(n_components=2)
X_pca = pca.fit_transform(X)print("解釋方差比:", pca.explained_variance_ratio_)
print("累計解釋方差:", np.cumsum(pca.explained_variance_ratio_))2.項目實戰
. 項目概述
本項目使用PCA(主成分分析)對鳶尾花數據集進行降維處理,然后使用邏輯回歸進行分類,并比較降維前后的分類效果。
2. 代碼實現與分析
2.1 數據準備與PCA降維
from sklearn.decomposition import PCA
import pandas as pd# 數據讀取
data = pd.read_excel(".\hua.xlsx")# 數據劃分
X = data.iloc[:,:-1] # 特征
y = data.iloc[:,-1] # 標簽# PCA實例化與訓練
pca = PCA(n_components=0.90) # 保留90%的方差
pca.fit(X) # 訓練PCA模型# 輸出PCA結果
print('特征所占百分比:{}'.format(sum(pca.explained_variance_ratio_)))
print(pca.explained_variance_ratio_) # 數據降維
new_x = pca.transform(X)
print('PCA降維后數據:')
print(new_x)2.2 數據分割與模型訓練
from sklearn.model_selection import train_test_split# 數據分割
x_train, x_test, y_train, y_test = train_test_split(new_x, y, test_size=0.2, random_state=0)# 邏輯回歸模型
from sklearn.linear_model import LogisticRegression
classifier = LogisticRegression()
classifier.fit(x_train, y_train)# 預測
train_pred = classifier.predict(x_train)
test_pred = classifier.predict(x_test)print("訓練集預測結果:", train_pred)
print("測試集預測結果:", test_pred)2.3 評估指標
from sklearn.metrics import classification_report# 訓練集評估
print("訓練集分類報告:")
print(classification_report(y_train, train_pred))# 測試集評估
print("測試集分類報告:")
print(classification_report(y_test, test_pred))3. PCA原理回顧
PCA(主成分分析)是一種常用的降維方法,其核心思想是通過線性變換將高維數據投影到低維空間,同時保留盡可能多的原始數據信息。
3.1 PCA關鍵步驟
1.??數據標準化??:將每個特征減去其均值
2.??計算協方差矩陣??:反映特征間的相關性
3.??特征值分解??:獲取特征值和特征向量
4.?選擇主成分??:按特征值大小排序,選擇前k個
5.??數據轉換??:將原始數據投影到主成分空間
3.2 數學原理
PCA的核心數學操作是協方差矩陣的特征分解:
通過找到矩陣P使得:
是一個對角矩陣,且對角元素按從大到小排列。
4. 結果分析與比較
4.1 降維前后模型性能比較
我們可以比較使用PCA降維前后模型的性能差異:
# 不降維的模型
x_train_raw, x_test_raw, y_train_raw, y_test_raw = train_test_split(X, y, test_size=0.2, random_state=0)classifier_raw = LogisticRegression()
classifier_raw.fit(x_train_raw, y_train_raw)raw_train_pred = classifier_raw.predict(x_train_raw)
raw_test_pred = classifier_raw.predict(x_test_raw)print("原始數據訓練集分類報告:")
print(classification_report(y_train_raw, raw_train_pred))
print("原始數據測試集分類報告:")
print(classification_report(y_test_raw, raw_test_pred))4.2 分析結論
- ?降維效果??:PCA可以有效減少特征維度,同時保留大部分信息
模型性能??:對于不同數據集,PCA可能提高或降低模型性能
大數據集:PCA可以提高計算效率,可能提升性能
小數據集:PCA可能丟失重要信息,降低性能
??實際應用??:需要根據具體數據集和任務需求決定是否使用PCA
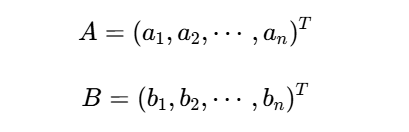
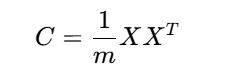



的一種方案)




——VGA顯示彩條和圖片)

![week2-[一維數組]出現次數](http://pic.xiahunao.cn/week2-[一維數組]出現次數)








