深度優先搜索(dfs)理論基礎
dfs就是可一個方向去搜直到盡頭再換方向,換方向的過程就涉及到了回溯。
代碼框架
因為dfs搜索可一個方向,并需要回溯,所以用遞歸的方式來實現是最方便的。
先來回顧一下回溯法的代碼框架:
void backtracking(參數) {if (終止條件) {存放結果;return;}for (選擇:本層集合中元素(樹中節點孩子的數量就是集合的大小)) {處理節點;backtracking(路徑,選擇列表); // 遞歸回溯,撤銷處理結果}
}據此給出dfs的代碼框架:
void dfs(參數) {if (終止條件) {存放結果;return;}for (選擇:本節點所連接的其他節點) {處理節點;dfs(圖,選擇的節點); // 遞歸回溯,撤銷處理結果}
}所有可達路徑
題目鏈接:98. 所有可達路徑 (kamacoder.com)
【題目描述】
給定一個有 n 個節點的有向無環圖,節點編號從 1 到 n。請編寫一個程序,找出并返回所有從節點 1 到節點 n 的路徑。每條路徑應以節點編號的列表形式表示。
【輸入描述】
第一行包含兩個整數 N,M,表示圖中擁有 N 個節點,M 條邊
后續 M 行,每行包含兩個整數 s 和 t,表示圖中的 s 節點與 t 節點中有一條路徑
【輸出描述】
輸出所有的可達路徑,路徑中所有節點的后面跟一個空格,每條路徑獨占一行,存在多條路徑,路徑輸出的順序可任意。
如果不存在任何一條路徑,則輸出 -1。
注意輸出的序列中,最后一個節點后面沒有空格! 例如正確的答案是?1 3 5,而不是?1 3 5, 5后面沒有空格!
輸入示例
5 5
1 3
3 5
1 2
2 4
4 5
輸出示例
1 3 5
1 2 4 5
提示信息
用例解釋:
有五個節點,其中的從 1 到達 5 的路徑有兩個,分別是 1 -> 3 -> 5 和 1 -> 2 -> 4 -> 5。
因為擁有多條路徑,所以輸出結果為:
1 3 5
1 2 4 5或
1 2 4 5
1 3 5
都算正確。數據范圍:
圖中不存在自環
圖中不存在平行邊
1 <= N <= 100
1 <= M <= 500
使用鄰接矩陣存儲
使用二維數組來表示圖,因為有n個節點,節點編號從1開始,所以我們申請(n+1)*(n+1)大的二維數組;然后構造m個邊:
int[][] graph=new int[n+1][n+1];
for(int i=0;i<m;i++){int a=in.nextInt();int b=in.nextInt();graph[a][b]=1;
}使用鄰接矩陣存儲dfs的代碼:
public static void dfs(List<List<Integer>> graph, int x, int n) { //x表示當前遍歷到的節點if (x == n) {res.add(new ArrayList<>(list));return;}for(int i=1;i<=n;i++){if(graph[x][i]==1){list.add(i);dfs(graph,i,n);list.remove(list.size()-1);}}}打印結果:
for(List<Integer> tmp:res){for(int i=0;i<tmp.size()-1;i++){System.out.print(tmp.get(i)+" ");}System.out.println(tmp.get(tmp.size()-1));
}整體代碼如下:
import java.util.*;public class Main{static List<List<Integer>> res=new ArrayList<List<Integer>>();static List<Integer> list=new ArrayList<>();public static void main(String[] args){Scanner in=new Scanner(System.in);int n=in.nextInt();int m=in.nextInt();int[][] graph=new int[n+1][n+1];for(int i=0;i<m;i++){int a=in.nextInt();int b=in.nextInt();graph[a][b]=1;}list.add(1);dfs(graph,1,n);if(res.isEmpty())System.out.println(-1);for(List<Integer> tmp:res){for(int i=0;i<tmp.size()-1;i++){System.out.print(tmp.get(i)+" ");}System.out.println(tmp.get(tmp.size()-1));}}public static void dfs(int[][] graph,int x,int n){//x表示當前遍歷到的節點if(x==n){res.add(new ArrayList<>(list));return;}for(int i=1;i<=n;i++){if(graph[x][i]==1){list.add(i);dfs(graph,i,n);list.remove(list.size()-1);}}}
}使用鄰接表存儲
List<List<Integer>> graph = new ArrayList<List<Integer>>(n + 1);for(int i=0;i<=n;i++){graph.add(new ArrayList<>());}for (int i = 0; i < m; i++) {int a = in.nextInt();int b = in.nextInt();graph.get(a).add(b);}使用領接表存儲的dfs的寫法:
public static void dfs(List<List<Integer>> graph, int x, int n) { //x表示當前遍歷到的節點if (x == n) {res.add(new ArrayList<>(list));return;}for (int i : graph.get(x)) {list.add(i);dfs(graph, i, n);list.remove(list.size() - 1);}}打印結果:
if (res.isEmpty()) System.out.println(-1);for (List<Integer> tmp : res) {for (int i = 0; i < tmp.size() - 1; i++) {System.out.print(tmp.get(i) + " ");}System.out.println(tmp.get(tmp.size() - 1));}整體代碼如下:
import java.util.*;public class Main {static List<List<Integer>> res = new ArrayList<List<Integer>>();static List<Integer> list = new ArrayList<>();public static void main(String[] args) {Scanner in = new Scanner(System.in);int n = in.nextInt();int m = in.nextInt();//鄰接表寫法List<List<Integer>> graph = new ArrayList<List<Integer>>(n + 1);for(int i=0;i<=n;i++){graph.add(new ArrayList<>());}for (int i = 0; i < m; i++) {int a = in.nextInt();int b = in.nextInt();graph.get(a).add(b);}list.add(1);dfs(graph, 1, n);if (res.isEmpty()) System.out.println(-1);for (List<Integer> tmp : res) {for (int i = 0; i < tmp.size() - 1; i++) {System.out.print(tmp.get(i) + " ");}System.out.println(tmp.get(tmp.size() - 1));}}public static void dfs(List<List<Integer>> graph, int x, int n) { //x表示當前遍歷到的節點if (x == n) {res.add(new ArrayList<>(list));return;}for (int i : graph.get(x)) {list.add(i);dfs(graph, i, n);list.remove(list.size() - 1);}}
}廣度優先搜索(bfs)理論基礎
bfs就是先把本節點所連接的所有節點遍歷一遍,走到下一個節點的時候,再把連接該節點的所有節點遍歷一遍,四面八方的搜索過程。
代碼模板
private static final int[][] dir = {{0, 1}, {1, 0}, {-1, 0}, {0, -1}};//表示四個方向
// grid 是地圖,也就是一個二維數組
// visited標記訪問過的節點,不要重復訪問
// x,y 表示開始搜索節點的下標public static void bfs(char[][] grid, boolean[][] visited, int x, int y) {// 定義隊列,存儲坐標對Queue<int[]> queue = new LinkedList<>();// 起始節點加入隊列queue.offer(new int[]{x, y});// 只要加入隊列,立刻標記為訪問過的節點visited[x][y] = true;// 開始遍歷隊列里的元素while (!queue.isEmpty()) {// 從隊列取出元素int[] current = queue.poll();int curx = current[0];int cury = current[1];// 向當前節點的四個方向(上下左右)遍歷for (int i = 0; i < 4; i++) {// 獲取周邊四個方向的坐標int nextx = curx + dir[i][0];int nexty = cury + dir[i][1];// 檢查坐標是否越界,如果越界直接跳過if (nextx < 0 || nextx >= grid.length || nexty < 0 || nexty >= grid[0].length) {continue;}// 如果節點沒被訪問過if (!visited[nextx][nexty]) {// 將該節點加入隊列,作為下一輪要遍歷的節點queue.offer(new int[]{nextx, nexty});// 只要加入隊列立刻標記,避免重復訪問visited[nextx][nexty] = true;}}}}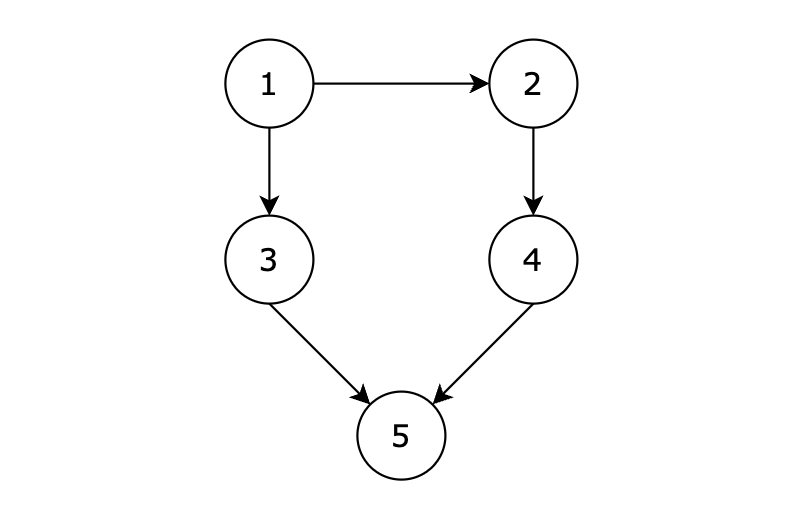





:RKNN-ToolKit2性能和內存評估)








詳解)


![[Chat-LangChain] 前端用戶界面 | 核心交互組件 | 會話流管理](http://pic.xiahunao.cn/[Chat-LangChain] 前端用戶界面 | 核心交互組件 | 會話流管理)

