【遞歸、搜索與回溯算法】DFS解決FloodFill算法

在這里插入圖片描述

FloodFill算法簡介
一、[圖像渲染](https://leetcode.cn/problems/flood-fill/description/)
二、[島嶼數量](https://leetcode.cn/problems/number-of-islands/description/)
三、[島嶼的最大面積](https://leetcode.cn/problems/max-area-of-island/description/)
四、[被圍繞的區域](https://leetcode.cn/problems/surrounded-regions/description/)
五、[太平洋大西洋水流問題](https://leetcode.cn/problems/pacific-atlantic-water-flow/description/)
六、[掃雷游戲](https://leetcode.cn/problems/minesweeper/description/)
七、[衣櫥整理](https://leetcode.cn/problems/ji-qi-ren-de-yun-dong-fan-wei-lcof/description/)
結尾

FloodFill算法簡介

Flood Fill 算法（漫水填充算法）是一種經典的圖像處理技術，用于將連通區域內的所有像素替換為指定顏色。

核心思想：

從起始點開始，遞歸或迭代地將與其連通且顏色相同的所有像素替換為目標顏色，直到所有連通像素被處理完畢。

一、圖像渲染

題目描述：

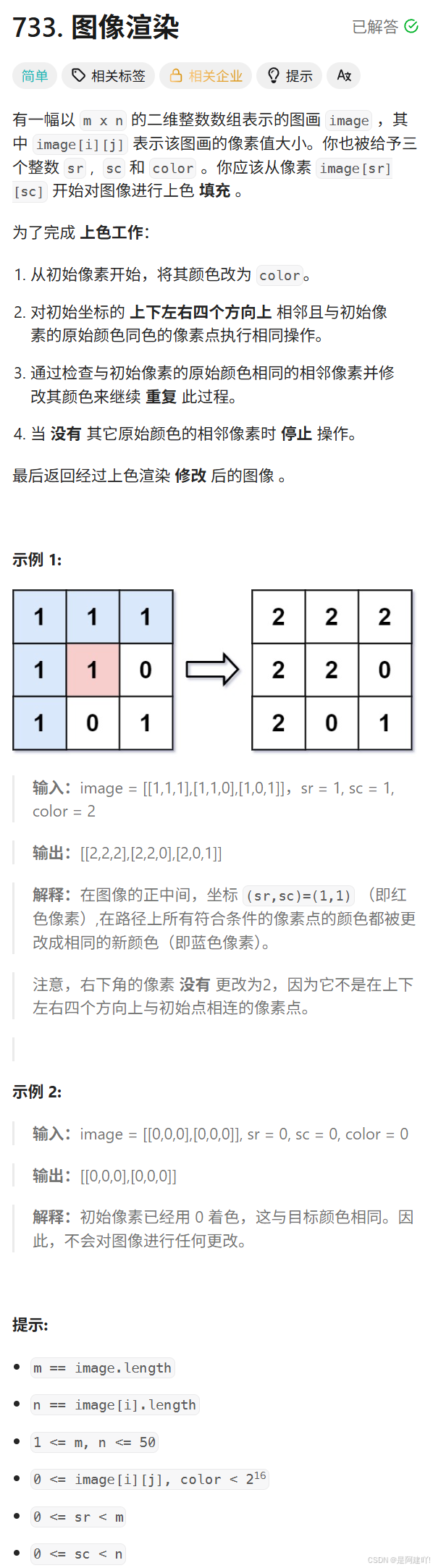
思路講解：
本道題會給我們起始點和目標顏色，讓我們將二維數組中起始點和與起始點連通并且與起始點顏色相同點的值修改為目標顏色，這里使用DFS解決，從指定初始像素出發，遞歸修改所有與初始像素原始顏色相同的連通像素，實現圖像的填充渲染。以下是具體思路：

全局變量：
- oldcolor：初始像素的原始顏色
- newcolor：目標填充顏色
- rows, cols：圖像的行數和列數
- dx, dy：方向數組，代表右、左、上、下四個移動方向
函數參數：
- image：原始圖像的二維數組
- row, col：當前正在處理的像素坐標
遞歸邏輯：
- 進入 dfs 后，首先將當前像素的顏色改為 newcolor
- 遍歷四個方向，計算新坐標，檢查其合法性：
  - 處于圖像邊界內
  - 像素顏色與 oldcolor 相同
- 對符合條件的相鄰像素調用 dfs 遞歸
- 無顯式回溯，因像素顏色被改為 newcolor 后，不會再與 oldcolor 匹配，自然避免重復處理，無需恢復狀態
終止條件：
- 當某一方向的相鄰像素超出邊界，或顏色與 oldcolor 不同時，該方向的遞歸自然終止

編寫代碼：

class Solution {int dx[4] = {0,0,-1,1};int dy[4] = {1,-1,0,0};int oldcolor , newcolor;int rows , cols;
public:void dfs(vector<vector<int>>& image , int row , int col){image[row][col] = newcolor;for(int i = 0 ; i < 4 ; i++){int x = row + dx[i] , y = col + dy[i];if(0 <= x && x < rows && 0 <= y && y < cols && image[x][y] == oldcolor){dfs(image,x,y);}}}vector<vector<int>> floodFill(vector<vector<int>>& image, int sr, int sc, int color) {oldcolor = image[sr][sc];newcolor = color;if(oldcolor == newcolor)    return image;rows = image.size() , cols = image[0].size();dfs(image,sr,sc);return image;}
};

二、島嶼數量

題目描述：

思路講解：
本道題需要我們找出島嶼的數量。我們可以通過遍歷網格中的陸地單元格，DFS遞歸探索其所有連通的陸地并標記訪問狀態，從而統計獨立島嶼的數量。以下是具體思路：

全局變量：
- dx，dy：方向數組，代表右、左、上、下四個移動方向
- vis：標記陸地單元格是否已被訪問
- rows，cols：記錄網格的行數和列數
遞歸邏輯：
- 進入 dfs 函數后，首先將當前陸地單元格標記為已訪問，防止后續重復探索
- 遍歷四個方向，計算相鄰單元格的坐標，并檢查其合法性：
  - 坐標在網格邊界內
  - 該單元格是未訪問的陸地
  - 對符合條件的相鄰陸地單元格遞歸調用 dfs，繼續探索其連通的所有陸地，直至該島嶼的所有陸地均被標記訪問
計數邏輯：
- 兩層循環遍歷網格中的每個單元格，若發現未訪問的陸地，說明找到一個新的獨立島嶼：
  - 島嶼計數器 ans 加 1
  - 調用 dfs 函數，遞歸標記該島嶼的所有連通陸地為已訪問
  - 遍歷結束后，返回網格中島嶼的總數

編寫代碼：

class Solution {int dx[4] = {0, 0, -1, 1};int dy[4] = {1, -1, 0, 0};int rows , cols;vector<vector<bool>> vis;
public:void dfs(vector<vector<char>>& grid , int row , int col){vis[row][col] = true;for(int i = 0 ; i < 4 ; i++){int x = row + dx[i] , y = col + dy[i];if(0 <= x && x < rows && 0 <= y && y < cols && grid[x][y] == '1' && vis[x][y] == false){dfs(grid,x,y);}}}int numIslands(vector<vector<char>>& grid) {rows = grid.size() , cols = grid[0].size();vis = vector<vector<bool>>(rows,vector<bool>(cols,false));int ans = 0;for(int i = 0 ; i < rows ; i++){for(int j = 0 ; j < cols ; j++){if(grid[i][j] == '1' && vis[i][j] == false){ans++;dfs(grid,i,j);}}}return ans;}
};

三、島嶼的最大面積

題目描述：

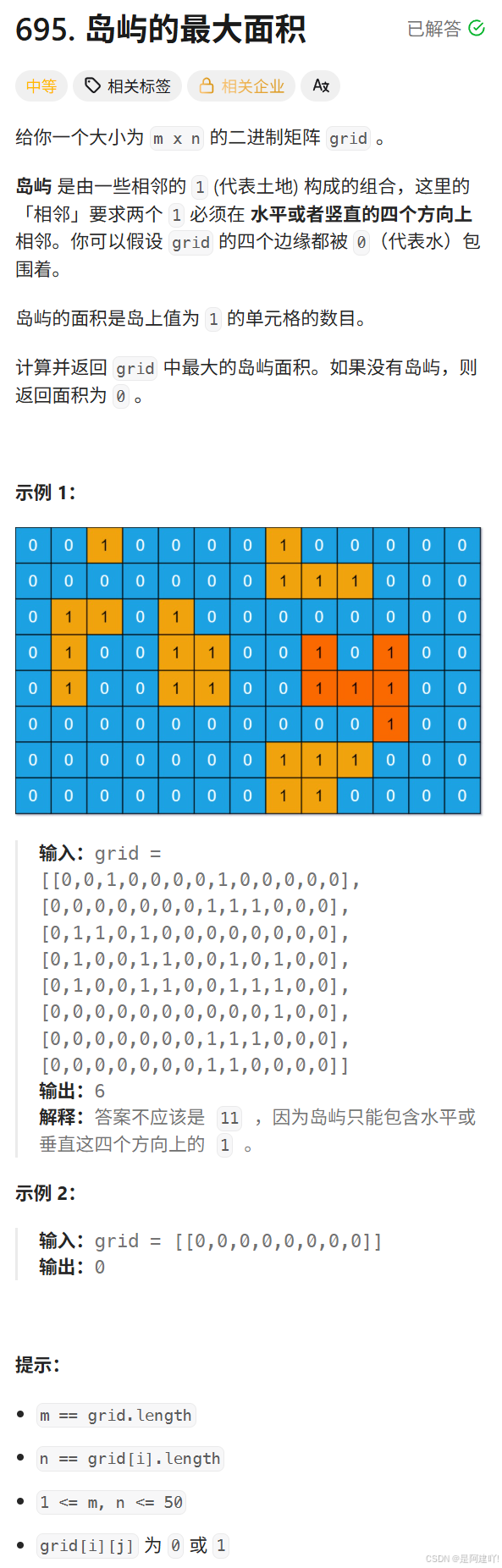
思路講解：

本道題需要我們找出島嶼的最大面積。我們可以通過遍歷網格中的陸地單元格，DFS遞歸探索每個島嶼的所有連通陸地，計算其面積并記錄最大值。以下是具體思路：

全局變量：
- dx，dy：方向數組，代表右、左、上、下四個移動方向
- vis：標記陸地單元格是否已被訪問
- rows，cols：記錄網格的行數和列數
遞歸邏輯：
- 進入 dfs 后，首先標記當前單元格為已訪問
- 當前陸地本身計數為 1
- 遍歷四個方向，計算相鄰單元格，檢查其合法性：
  - 坐標在網格邊界內
  - 該單元格是未訪問的陸地
- 對符合條件的相鄰陸地，遞歸調用 dfs 并將返回的面積累加到 ret 中
- 遞歸結束后，ret 即為當前島嶼的總面積，返回給上一層
計算最大面積邏輯：
- 兩層遍歷網格中的每個單元格：
  - 若發現未訪問的陸地，調用 dfs 計算該島嶼的面積
  - 用當前島嶼面積更新最大面積
  - 遍歷結束后，返回網格中最大的島嶼面積

編寫代碼：

class Solution {int dx[4] = {0,0,-1,1};int dy[4] = {1,-1,0,0};vector<vector<bool>> vis;int rows , cols;
public:int dfs(vector<vector<int>>& grid , int row , int col){vis[row][col] = true;int ret = 1;for(int i = 0 ; i < 4 ; i++){int x = row + dx[i] , y = col + dy[i];if(0 <= x && x < rows && 0 <= y && y < cols && grid[x][y] == 1 && vis[x][y] == false){ret += dfs(grid,x,y);}}return ret;}int maxAreaOfIsland(vector<vector<int>>& grid) {rows = grid.size() , cols = grid[0].size();vis = vector<vector<bool>>(rows,vector<bool> (cols,false));int ans = 0;for(int i = 0 ; i < rows ; i++){for(int j = 0 ; j < cols ; j++){if(grid[i][j] == 1 && vis[i][j] == false){ans = max(ans , dfs(grid,i,j));}}}return ans;}
};

四、被圍繞的區域

題目描述：

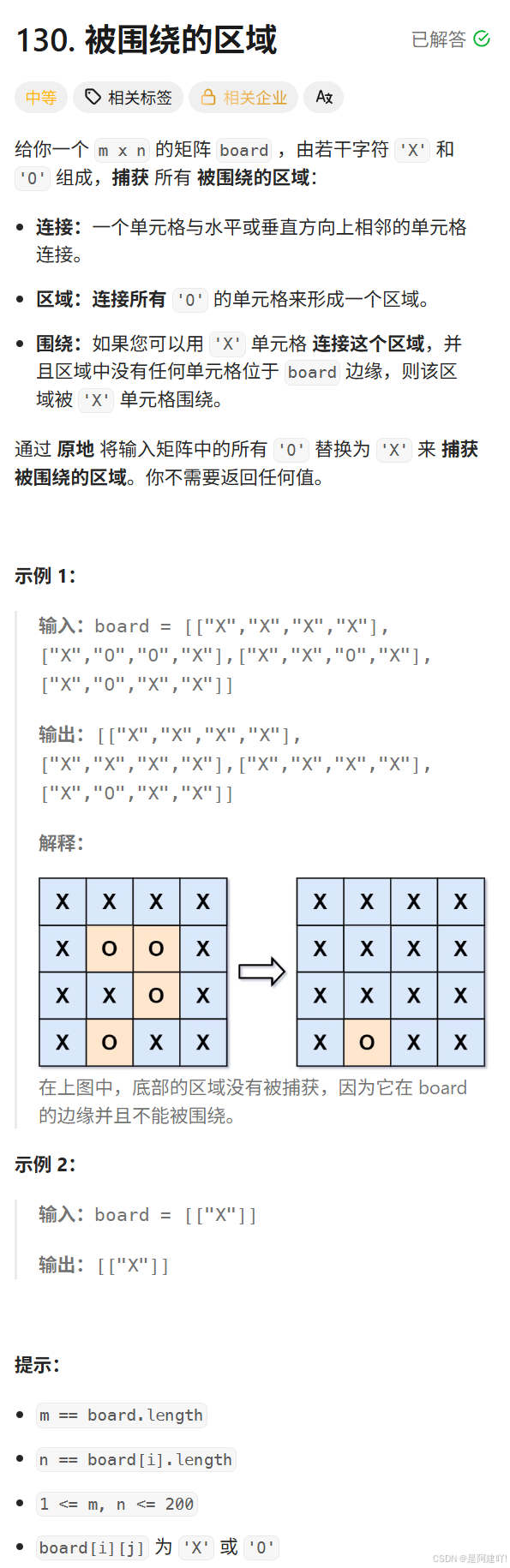
思路講解：
本道題給我們一個二維數組，想讓我們將被 ‘X’ 包圍的 'O’區域中的 ‘O’ 全部替換為 ‘X’，但是想直接找到被 ‘X’ 包圍的 ‘O’ 并替換為 'X’需要兩個步驟，首先是通過一次DFS判斷該區域是否被包圍，再通過一次DFS將被 ‘X’ 包圍的 ‘O’ 替換為 ‘X’。

正向麻煩的話，就可以反向思考。先找出所有不被圍繞的 ‘O’（即位于二維數組邊緣或與邊緣 ‘O’ 相連的 ‘O’），并將這些 ‘O’ 替換處 ‘O’ 和 ‘X’ 以外的字符；然后將剩余的 ‘O’（被圍繞的區域）替換為 ‘X’。以下是具體思路：

全局變量：
- dx，dy：方向數組，代表右、左、上、下四個移動方向
- vis：標記已處理的 “O” 單元格
- rows，cols：記錄網格的行數和列數
遞歸邏輯：
- 進入 dfs 后，將當前邊緣相連的 “O” 單元格標記為 ‘H’
- 遍歷四個方向，計算相鄰單元格，檢查其合法性：
  - 坐標在網格邊界內
  - 該單元格是未訪問的 “O”
  - 對符合條件的相鄰 “O”，標記為已訪問后遞歸調用 dfs，繼續標記其連通的 “O” 為 ‘H’，直至所有與邊緣相連的 “O” 均被標記
完整思路：
- 遍歷網格的四條邊緣（第一行、最后一行、第一列、最后一列），對邊緣上的 “O” 啟動 DFS，將其及所有連通的 “O” 標記為 ‘H’
- 遍歷整個網格，將剩余未被標記為 ‘H’ 的 “O”替換為 ‘X’
- 將臨時標記為 ‘H’ 的單元格恢復為 ‘O’，最終得到僅保留未被圍繞 “O” 的網格

編寫代碼：

class Solution {int dx[4] = {0, 0, -1, 1};int dy[4] = {1, -1, 0, 0};int rows, cols;
public:void dfs(vector<vector<char>>& board, vector<vector<bool>>& vis, int row, int col) {board[row][col] = 'H';for (int i = 0; i < 4; i++) {int x = row + dx[i], y = col + dy[i];if (x >= 0 && x < rows && y >= 0 && y < cols && board[x][y] == 'O' && vis[x][y] == false) {vis[x][y] = true;dfs(board,vis,x,y);}}}void solve(vector<vector<char>>& board) {rows = board.size(), cols = board[0].size();vector<vector<bool>> vis(rows, vector<bool>(cols, false));for (int i = 0; i < cols; i++) {if (board[0][i] == 'O' && vis[0][i] == false) {dfs(board, vis, 0 , i);}if (board[rows - 1][i] == 'O' && vis[rows - 1][i] == false) {dfs(board, vis, rows - 1, i);}}for (int i = 0; i < rows; i++) {if (board[i][0] == 'O' && vis[i][0] == false) {dfs(board, vis, i, 0);}if (board[i][cols - 1] == 'O' && vis[i][cols - 1] == false) {dfs(board, vis, i, cols - 1);}}for (int i = 0; i < rows; i++) {for (int j = 0; j < cols; j++) {if (board[i][j] == 'O')board[i][j] = 'X';else if (board[i][j] == 'H')board[i][j] = 'O';}}}
};

五、太平洋大西洋水流問題

題目描述：

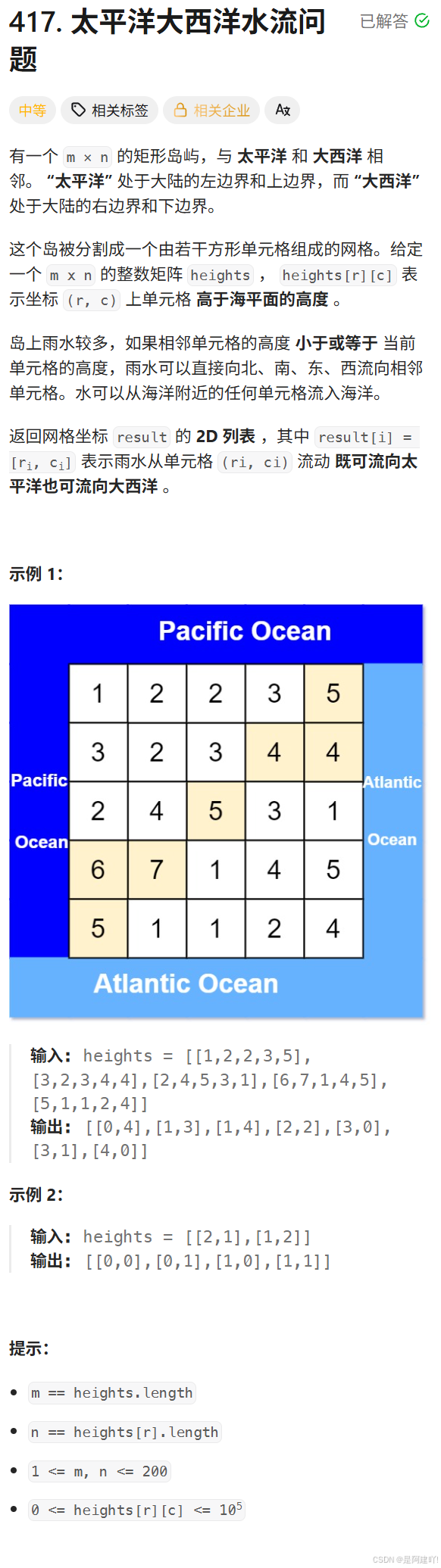
思路講解：
本道題需要我們找到所有既可流向太平洋又可流向大西洋的單元格。首先想到的思路就是通過遞歸判斷每一個單元格是否滿足流向太平洋和大西洋，但是這樣會有很多重復路徑，導致時間復雜度顯著提高。那么我們就轉換一下思路，分別標記能流向太平洋和大西洋的單元格，最終取兩者的交集得到既可流向太平洋又可流向大西洋的單元格，以下是具體思路：

全局變量：
- dx，dy：方向數組，代表右、左、上、下四個移動方向
- rows，cols：記錄網格的行數和列數
遞歸邏輯：
- 進入 dfs 后，將當前單元格在對應海洋的標記矩陣中設為 true
- 遍歷四個方向，計算相鄰單元格，檢查其是否符合 “能流向當前單元格” 的條件
  - 坐標在網格邊界內
  - 相鄰單元格高度 >= 當前單元格高度
  - 相鄰單元格尚未被標記為可流向目標海洋
  - 對符合條件的相鄰單元格遞歸調用 dfs，繼續標記其是否能流向目標海洋，直至所有可達單元格均被標記
完整流程：
- 創建 pacific 和 atlantic 兩個布爾矩陣，初始均為 false
- 太平洋：從左邊界和上邊界的所有單元格啟動 DFS，標記所有能流向太平洋的單元格
- 大西洋：從右邊界和下邊界的所有單元格啟動 DFS，標記所有能流向大西洋的單元格
- 遍歷網格，收集所有在 pacific 和 atlantic 中均被標記為 true 的單元格坐標，即為結果

編寫代碼：

class Solution {int dx[4] = {0,0,-1,1};int dy[4] = {1,-1,0,0};int rows , cols;
public:void dfs(vector<vector<int>>& heights, vector<vector<bool>>& ocean , int row , int col){ocean[row][col] = true;for(int i = 0 ; i < 4 ; i++){int x = row + dx[i] , y = col + dy[i];if(0 <= x && x < rows && 0 <= y && y < cols && heights[row][col] <= heights[x][y] && ocean[x][y] == false){dfs(heights,ocean,x,y);}}}vector<vector<int>> pacificAtlantic(vector<vector<int>>& heights) {vector<vector<int>> ans;rows = heights.size() , cols = heights[0].size();vector<vector<bool>>pacific (rows,vector<bool>(cols,false));vector<vector<bool>>atlantic(rows,vector<bool>(cols,false));for(int i = 0 ; i < rows ; i++){dfs(heights,pacific,i,0);dfs(heights,atlantic,i,cols-1);}for(int i = 0 ; i < cols ; i++){dfs(heights,pacific,0,i);dfs(heights,atlantic,rows-1,i);}for(int i = 0 ; i < rows ; i++){for(int j = 0 ; j < cols ; j++){if(pacific[i][j] && atlantic[i][j]){ans.push_back({i,j});}}}return ans;}
};

六、掃雷游戲

題目描述：

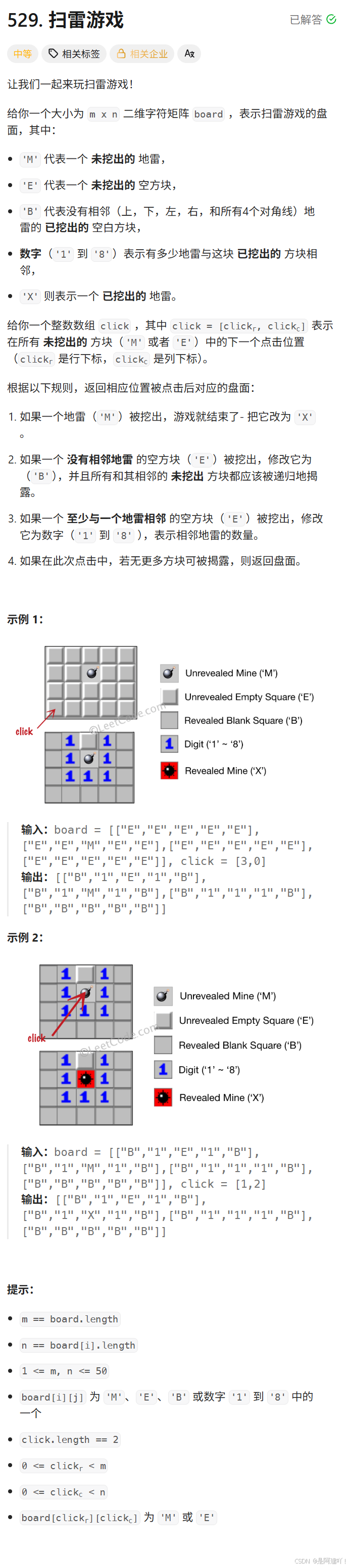
思路講解：
本道題需要我們完成掃雷游戲，我們只需要根據點擊位置的不同類型執行相應規則即可。以下是具體思路：

全局變量：
- dx，dy：方向數組，代表8 個方向的坐標偏移（上下、左右、4 個對角線）移動方向
- vis：標記已處理的單元格
- rows，cols：記錄盤面的行數和列數
遞歸邏輯：
- 進入 dfs 后，首先標記當前單元格為已訪問，防止重復處理
- 遍歷 8 個方向，統計當前單元格周圍未挖出的地雷（“M”）數量 num
- 更新當前單元格狀態：
  - 若 num > 0，當前單元格修改為對應數字字符，且停止遞歸
  - 若 num == 0，當前單元格修改為 “B”，繼續探索相鄰方塊
  - 對 8 個方向中未訪問的相鄰單元格（“E”），遞歸調用 dfs 進行處理，直至所有可揭露的方塊均被處理
整體流程：
- 若點擊位置是地雷（“M”），直接將其改為 “X”（已挖出的地雷），游戲結束
- 若點擊位置是空方塊（“E”），啟動 DFS 遞歸處理，揭露該方塊及所有可探索的相鄰方塊
- 完成所有遞歸處理后，返回修改后的 board

編寫代碼：

class Solution {int dx[8] = {0,0,-1,1,-1,1,-1,1};int dy[8] = {1,-1,0,0,1,1,-1,-1};int rows , cols;vector<vector<bool>> vis;
public:void dfs(vector<vector<char>>& board, int row , int col){vis[row][col] = true;int num = 0;for(int i = 0 ; i < 8 ; i++){int x = row + dx[i] , y = col + dy[i];if(0 <= x && x < rows && 0 <= y && y < cols && board[x][y] == 'M'){num++;}}if(num == 0){board[row][col] = 'B';}else {board[row][col] = num + '0';return;}for(int i = 0 ; i < 8 ; i++){int x = row + dx[i] , y = col + dy[i];if(0 <= x && x < rows && 0 <= y && y < cols && vis[x][y] == false){dfs(board,x,y);}}}vector<vector<char>> updateBoard(vector<vector<char>>& board, vector<int>& click) {int row = click[0] , col = click[1];rows = board.size() , cols = board[0].size();vis = vector<vector<bool>>(rows,vector<bool>(cols,false));if(board[row][col] == 'M'){board[row][col] = 'X';}else{dfs(board,row,col);}return board;}
};

七、衣櫥整理

題目描述：

思路講解：
本道題需要我們找出需要整理格子的數量，我們可以從衣柜的起始位置 (0,0) 開始，遞歸探索所有符合整理條件的格子，統計需要整理的格子總數。以下是具體思路：

全局變量：
- dx，dy：方向數組，代表右、左、上、下四個移動方向
- vis：標記已整理的格子
- rows，cols：記錄網格的行數和列數
- ans：記錄需要整理的格子總數
遞歸邏輯：
- 進入dfs后，首先將當前格子計入整理總數，并標記為已訪問
- 遍歷四個方向，計算相鄰格子坐標，檢查其是否符合整理條件：
  - 坐標在衣柜邊界內
  - 未被整理過
  - 數位和滿足條件
- 對符合條件的相鄰格子遞歸調用dfs，繼續探索并計數，直至所有可達的符合條件的格子均被處理

編寫代碼：

class Solution {int dx[4] = {0,0,-1,1};int dy[4] = {1,-1,0,0};vector<vector<bool>> vis;int rows , cols;int ans = 0;
public:int getsum(int num){int sum = 0;while(num){sum += num % 10;num /= 10;}return sum;}void dfs(int row , int col , int cnt){ans++;vis[row][col] = true;for(int i = 0 ; i < 4 ; i++){int x = row + dx[i] , y = col + dy[i];if( 0 <= x && x < rows && 0 <= y && y < cols && getsum(x) + getsum(y) <= cnt && vis[x][y] == false){dfs(x,y,cnt);}}}int wardrobeFinishing(int m, int n, int cnt) {rows = m , cols = n;vis = vector<vector<bool>>(m,vector<bool>(n,false));dfs(0,0,cnt);return ans;}   
};