ODE-by-Matlab-01-人口增長模型

博客地址：Matlab微分方程01-模型

馬爾薩斯模型

馬爾薩斯模型是人口增長模型中最簡單的模型，它由英國牧師家馬爾薩斯在1798年提出。
他利用在教堂工作的機會，收集英國100多年的人口數據，發現人口的相對增長率是常數。
在這個基礎上，建立了一個描述人口增長的模型，也就是著名的“馬爾薩斯人口模型”。

在這個模型中，最重要的額概念是相對增長率。

$u˙u=r\frac{\dot{u}}{u} = r$

這里就涉及到微分的概念，變量 $u$ 對時間 $t$ 的導數，也就是變化率(這里可以稱之為增長率)，記作 $u˙\dot{u}$ 。

$u˙=dudt\dot{u} = \frac{du}{dt}$

那么“馬爾薩斯人口模型”表達為微分方程是這樣的形式。

$dudtu=α→dudt=αu\frac{\frac{du}{dt}}{u} = \alpha \rightarrow \frac{du}{dt} = \alpha u$

其中，時間為 $t$ ，人口 $u$ 為依賴于時間的函數，相對增長率是 $α\alpha$ （ $α>0\alpha >0$ ）。

這個方程的解很容易通過不定積分求解。

$∫duu=∫αdt→ln?u=αt+C→u(t)=eαt+C=neαt\int \frac{du}{u} = \int \alpha dt \rightarrow \ln u = \alpha t + C \rightarrow u(t) = e^{\alpha t + C} = n e^{\alpha t}$

這個解是一個指數函數！眾所周知，指數函數的增長是非常快的。這在一定的程度上導致了社會主義國家考慮對人口增長進行控制。

n = 81;
t = linspace(0, 100, 100);
alpha = 0.02; % 人口增長率
% 馬爾薩斯人口模型
u = n * exp(alpha * t);
figure;
plot(t, u , 'b-', 'LineWidth', 2);
xlabel('時間(年)');
ylabel('人口(億)');
title('馬爾薩斯人口模型')
grid on;
% 保存圖像  
exportgraphics(gcf, 'chp01/malthus_population_model.png', 'Resolution', 300);

在這里插入圖片描述

UN預測數據

我們可以從UN官網下載人口預測數據。
數據的格式是csv，第二表格包含了世界各國從2025年到2100年的人口預測數據。

我們通過websave命令下載數據，并用readtable命令讀取數據。注意實際的數據位置、文件名可能會發生改變，需要根據實際情況修改。

UN_Projection_File = 'https://population.un.org/wpp/assets/Excel%20Files/1_Indicator%20(Standard)/EXCEL_FILES/1_General/WPP2024_GEN_F01_DEMOGRAPHIC_INDICATORS_COMPACT.xlsx';
% 下載UN人口預測數據
if ~exist('chp01/WPP2024_GEN_F01_DEMOGRAPHIC_INDICATORS_COMPACT.xlsx', 'file')websave('chp01/WPP2024_GEN_F01_DEMOGRAPHIC_INDICATORS_COMPACT.xlsx', UN_Projection_File);
end% 讀取UN人口預測數據, sheet 'Medium variant', range 'L18:94': total population, K18:94: Years
if ~exist('chp01/WPP2024_GEN_F01_DEMOGRAPHIC_INDICATORS_COMPACT.xlsx', 'file')error('UN人口預測數據文件未找到，請檢查下載路徑。');
end
data = readtable('chp01/WPP2024_GEN_F01_DEMOGRAPHIC_INDICATORS_COMPACT.xlsx', ...'Sheet', 'Medium variant', 'Range', 'K18:L94');

然后我們來看看，馬爾薩斯模型數據與UN預測數據的差異。

% 提取年份和人口數據
years = data{:, 1};
population = data{:, 2} * 1e3 * 1e-8; % 單位為千人-->億% 繪制UN人口預測數據
figure; 
plot(years, population, 'k-', 'LineWidth', 2);
xlabel('年份');
ylabel('人口(億)');
title('聯合國人口預測');
grid on;
legends = {'UN Population Projection'};hold on;
% 繪制擬合的線性模型alphas = linspace(0.001, 0.01, 5); % 人口增長率范圍for idx = 1:length(alphas)alphai = alphas(idx);% 使用馬爾薩斯模型擬合UN人口預測數據iyears = years - years(1); % 將年份歸一化u = population(1) * exp(alphai * iyears); % 初始人口為第一個年份的人口    % 繪制擬合曲線plot(years, u, 'DisplayName', ['alpha = ', num2str(alphai)], 'LineWidth', 1.0);legends{end + 1} = ['alpha = ', num2str(alphai)]; %#ok<*SAGROW>
endlegend(legends, 'Location', 'best');% 保存圖像
exportgraphics(gcf, 'chp01/un_population_projection.png', 'Resolution', 300);

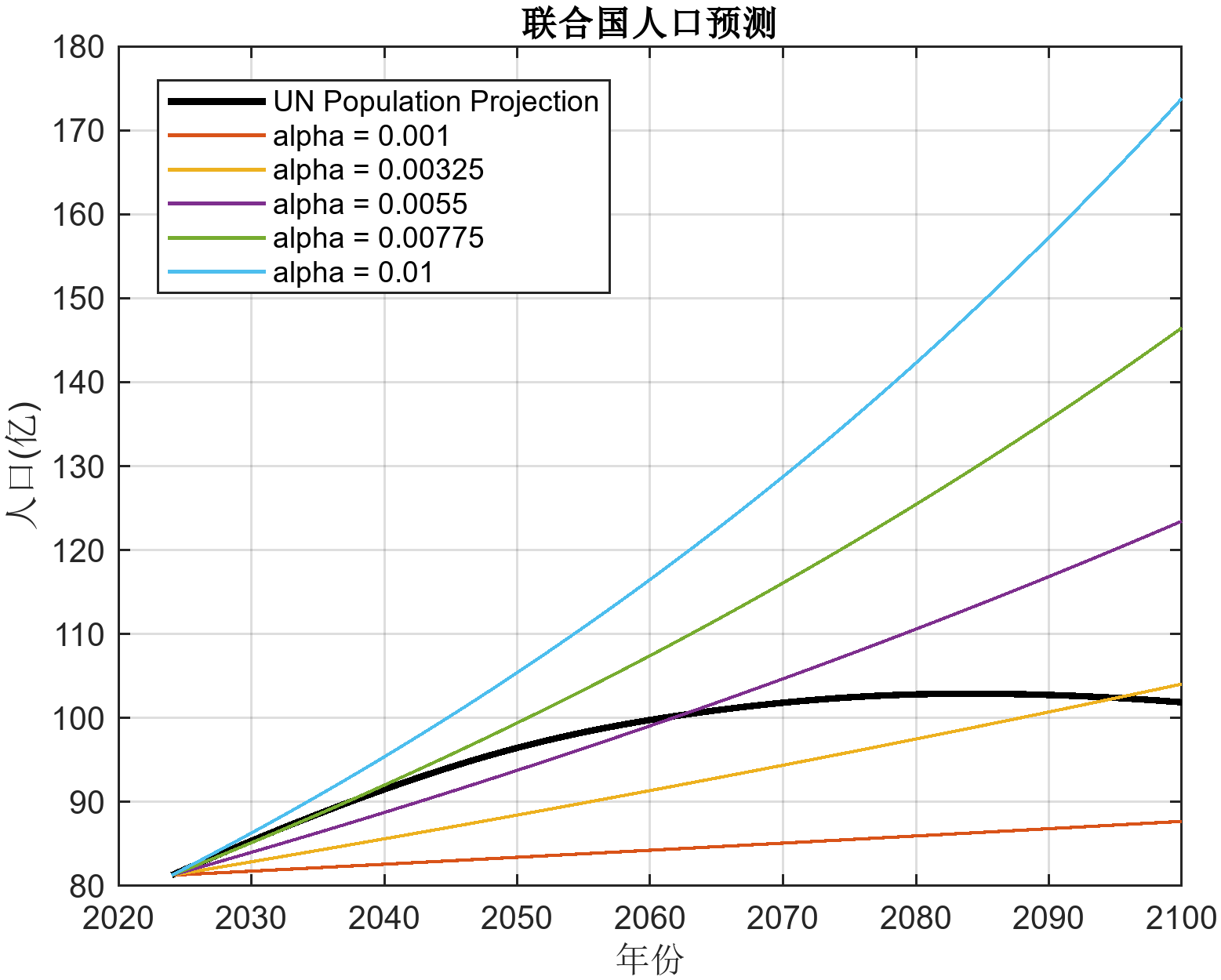
外鏈圖片轉存失敗,源站可能有防盜鏈機制,建議將圖片保存下來直接上傳

增長率從0.001到0.01的馬爾薩斯模型預測數據跟UN的預測有很大的區別，從圖上看趨勢都是不正確的。
聯合國的預測中，人口會達到一個飽和值（峰值），并在其后緩慢下降。

本質上來講，馬爾薩斯模型僅僅考慮人口相對增長率的線性特征，沒有考慮非線性的飽和特征。也就是，在人口較少時，人口的增長所受的限制很少，能夠出現指數增長；而當人口達到一定的數量是，生存環境、生態資源、社會因素等都會對人口增長產生限制，導致人口增長率逐漸減小，最終趨近于0。

但是，我們并不能說馬爾薩斯模型是錯誤的，因為馬爾薩斯模型是線性的，它實際上能夠很好的預測早期人口增長（例如英國工業革命帶來的人口增長），實際上，從前面的UN數據和馬爾薩斯模型擬合曲線中，我們也可以看到，馬爾薩斯模型能夠很好的預測早期人口增長。

這反映了微分方程模型的適用范圍問題。在其適用條件和假設成立的范圍內，模型能夠準確描述系統的動態行為；但當系統偏離這些基本假設時，模型的預測能力將顯著降低。這是數學建模中普遍存在的局限性。

基于以上分析，我們需要構建一個能夠刻畫人口增長非線性特征的數學模型，以更準確地描述人口動態變化規律。這就引出了下面將要介紹的Logistic模型。

Logistic模型

Logistic模型為什么叫做Logistic模型呢？因為它的解是一個Logistic函數。什么叫Logistic函數呢？它的形式是這樣的：

$\frac{L}{1 + e^{-k(x - x_0)}}$

這里 $L$ 是函數的最大值， $k$ 是增長率， $x_0$ 是函數的中點。

figure;
% Plot Logistic function
t = linspace(0, 100, 100);
L = 10; % 最大人口
K = 0.1; % 資源限制plot(t, L ./ (1 + exp(-K * (t - 50))), 'r-', 'LineWidth', 2);
xlabel('時間(年)');
ylabel('人口(億)');
title('Logistic Population Model');
grid on;% 保存圖像
exportgraphics(gcf, 'chp01/logistic_population_model.png', 'Resolution', 300);

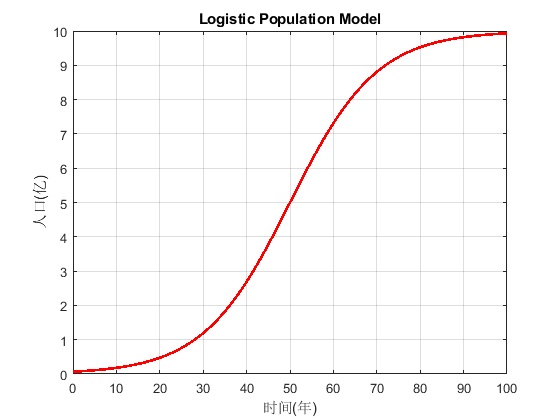
外鏈圖片轉存失敗,源站可能有防盜鏈機制,建議將圖片保存下來直接上傳

至于這個函數為什么叫做Logistic函數呢？

因為法國數學家 Pierre Fran?ois Verhulst就是這么命名的，他在1845年的論文（居然還有電子版可以看……）提出了這個函數來描述人口增長。這個論文現在還可以看到電子版，是法語的。在這論文電子版的地54也，作者比較了他的模型和馬爾薩斯模型，并在圖上給出了Logarithmique vs. Logistique的曲線命名。

在這里插入圖片描述

Verhulst在論文里面寫到：Nous donnerons le nom de logistique à la courbe (voyez la figure) caractérisée par l’équation précédente. 就是什么我們給前述方程給出的曲線（如圖）命名為Logistic曲線之類……

說到底就是他給這個函數起了個名字……

我看了好多地方，都沒有找到為什么叫logistique……

反正這個跟后勤（logistics）沒有關系。國外網友猜測這個跟logistique的詞源有關，logistique是法語，源自拉丁語logisticus，意思是“計算的”，而這個函數的計算……我編不出來了……

Verhulst的原始推導

現在我們來看看Verhulst是如何推導出Logistic模型的，這里我們遵循他在1845年論文中的原始推導。

Verhulst首先稱，馬爾薩斯的 $Mdppdt=l\frac{Mdp}{pdt}=l$ 并不正確，他給出一個修正的增長方程。

$Mdppdt=l?n(p?b)(2)\frac{M dp}{p dt} = l - n(p - b) \tag{2}$

這里 $M$ , $l$ , $n$ , $b$ 都是常數， $p$ 是人口， $t$ 是時間。

他接著寫道：d’où, en posant, pour abréger, $m = l + nb$ （為了簡化，設 $m = l + nb$ ），

$Mdppdt=m?np\frac{M dp}{p dt} = m - np$

然后得到：

$\frac{M dp}{mp - np^2} \tag{3}$

這個方程經過積分后（Cette équation étant intégrée donne），在觀察到當 $t = 0$ 時對應 $p = b$ 的條件下，得到：

$\frac{1}{m} \log_e \left[ \frac{p(m - nb)}{b(m - np)} \right] \tag{4}$

這就是Verhulst在他的原始論文中推導出的積分形式的解。

從這個積分方程可以反解得到人口 $p$ 關于時間 $t$ 的顯式表達式，這就是我們今天所知的Logistic函數。

傳染病問題

% 編制一個在二維網格中的小老鼠染病模擬
% M只老鼠，N只有傳染病，可以通過接觸傳染給健康的老鼠，
% 老鼠在[0,1]x[0,1]的二維網格中隨機分布，并且隨機運動
% 當二者距離小于0.01時，健康的老鼠有0.1的概率被感染
M = 500; % 老鼠數量
N = 1; % 傳染病數量
% 初始化老鼠位置和狀態
positions = rand(M, 2); % 老鼠位置
states = zeros(M, 1); % 0: 健康, 1: 感染
infected_indices = randperm(M, N); % 隨機選擇N只老鼠
states(infected_indices) = 1; % 設置感染狀態% 模擬老鼠運動和傳染
num_steps = 140; % 模擬步數history_infected = zeros(num_steps, M); % 記錄每一步的感染狀態
history_infected(1, :) = states; % 初始狀態
position_history = zeros(num_steps, M, 2); % 記錄每一步的位置
position_history(1, :, :) = positions; % 初始位置for step = 2:num_steps% 更新老鼠位置positions = positions + randn(M, 2) * 0.04; % 隨機運動positions = mod(positions, 1); % 保持在[0,1]范圍內% 檢查感染傳播for i = 1:Mif states(i) == 0 % 如果是健康的老鼠% 找到所有感染的老鼠infected_positions = positions(states == 1, :);distances = sqrt(sum((infected_positions - positions(i, :)).^2, 2));% 如果距離小于0.01且有感染概率，則感染if any(distances < 0.01) && rand < 0.8states(i) = 1; % 感染endendendhistory_infected(step, :) = states; % 記錄當前狀態position_history(step, :, :) = positions; % 記錄當前位置信息
endfigure;
plot(1:num_steps, sum(history_infected, 2), 'b-', 'LineWidth', 2);
xlabel('時間步');
ylabel('感染老鼠數量');
title('老鼠傳染病傳播模擬');
grid on;exportgraphics(gcf, 'chp01/mouse_infection_simulation.png', 'Resolution', 300);

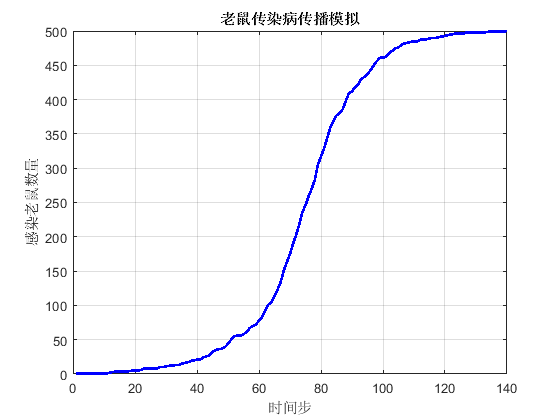
外鏈圖片轉存失敗,源站可能有防盜鏈機制,建議將圖片保存下來直接上傳

實際上，無聊的話，還可以整一個老鼠傳染病傳播模擬，代碼如下：

% 繪制初始狀態
states = history_infected(1, :); % 獲取初始狀態
positions = squeeze(position_history(1, :, :)); % 獲取初始位置
% 創建圖形窗口
figure("Visible", 'off'); % 顯示圖形窗口
scatter(positions(:, 1), positions(:, 2), 50, states, 'filled');
title(['老鼠感染試驗 - 時間 ', num2str(1), ' 感染老鼠數量: ', num2str(sum(states)), '/', num2str(M)]);
grid off;
box on; % 關閉網格線
axis off; % 關閉坐標軸顯示
xlim([0 1]);
ylim([0 1]);
% 保存初始狀態圖像
fn = 'chp01/mouse_initial_distribution.gif';
if exist(fn, 'file')delete(fn); % 刪除舊的文件
end
resolution = 100;
exportgraphics(gcf, fn , 'Resolution', resolution, 'Append', false);for step = 2:num_stepsstates = history_infected(step, :); % 獲取當前步的狀態positions = squeeze(position_history(step, :, :)); % 獲取當前步的位置% 繪制當前狀態scatter(positions(:, 1), positions(:, 2), 50, states, 'filled');title(['老鼠感染試驗 - 時間 ', num2str(step), ' 感染老鼠數量: ', num2str(sum(states)), '/', num2str(M)]);grid on;box on; % 關閉網格線axis off; % 關閉坐標軸顯示xlim([0 1]);ylim([0 1]);% 保存每一步的圖像exportgraphics(gcf, fn, 'Resolution', resolution, 'Append', true);
end