【機器學習-4】 | 集成學習 / 隨機森林篇

集成學習與隨機森林學習筆記

0 序言

本文將系統介紹Bagging、Boosting兩種集成學習方法及隨機森林算法，涵蓋其原理、過程、參數等內容。通過學習，你能理解兩種方法的區別，掌握隨機森林的隨機含義、算法步驟、優點及關鍵參數使用，明確各知識點的邏輯關聯，本篇將主要圍繞原理方面展開，下篇文章再具體用一個項目來加深鞏固本文提到的隨機森林算法。

1 Bagging（套袋法）

1.1 算法過程

樣本抽取：采用Bootstrapping方法從原始樣本集隨機抽取n個訓練樣本，經過k輪抽取，得到k個相互獨立且元素可重復的訓練集。這樣做是為了獲得不同的訓練數據，為后續構建多樣化模型做準備。

舉個例子：假設原始樣本集是學生成績數據集，包含 100 名學生的語文、數學、英語成績（即(n = 100) ），要進行(k = 5)輪抽取。
每一輪都從這 100 條數據里，有放回地隨機選 100 條，就像抽獎箱里有 100 個寫著學生成績的球，每次摸一個記錄后再放回去，摸 100 次組成一輪的訓練集。
5 輪后，得到 5 個訓練集，每個訓練集都是 100 條數據，數據可能有重復，也可能有遺漏，它們相互獨立，為后續訓練不同模型提供多樣數據。

模型訓練：使用得到的k個訓練集分別訓練k個模型，這里的模型可以是決策樹、KNN等。通過多個模型的訓練，能夠綜合不同模型的優勢。

舉個例子：接著上面學生成績的例子，用 5 個訓練集，分別訓練 5 個決策樹模型。
每個決策樹依據各自訓練集里的成績數據，學習如何根據語文、數學成績去判斷學生的英語成績等級。因為訓練集不同，每個決策樹學到的判斷邏輯會有差異，后續就能綜合這些差異模型的能力。

結果判定：在分類問題中，通過投票表決來確定最終結果，且所有模型的重要性相同。這是因為各模型是基于不同訓練集獨立訓練的，地位平等。

舉個例子：還是學生成績分類任務，5 個決策樹模型分別對一名新學生的成績輸出判斷。
比如模型 1 認為是A 等，模型 2 認為是B 等，模型 3 認為是A 等，模型 4 認為是A 等，模型 5 認為是B 等 。
統計投票，A 等得 3 票，B 等得 2 票，最終就判定該學生英語等級為A 等，每個模型一票，公平表決。

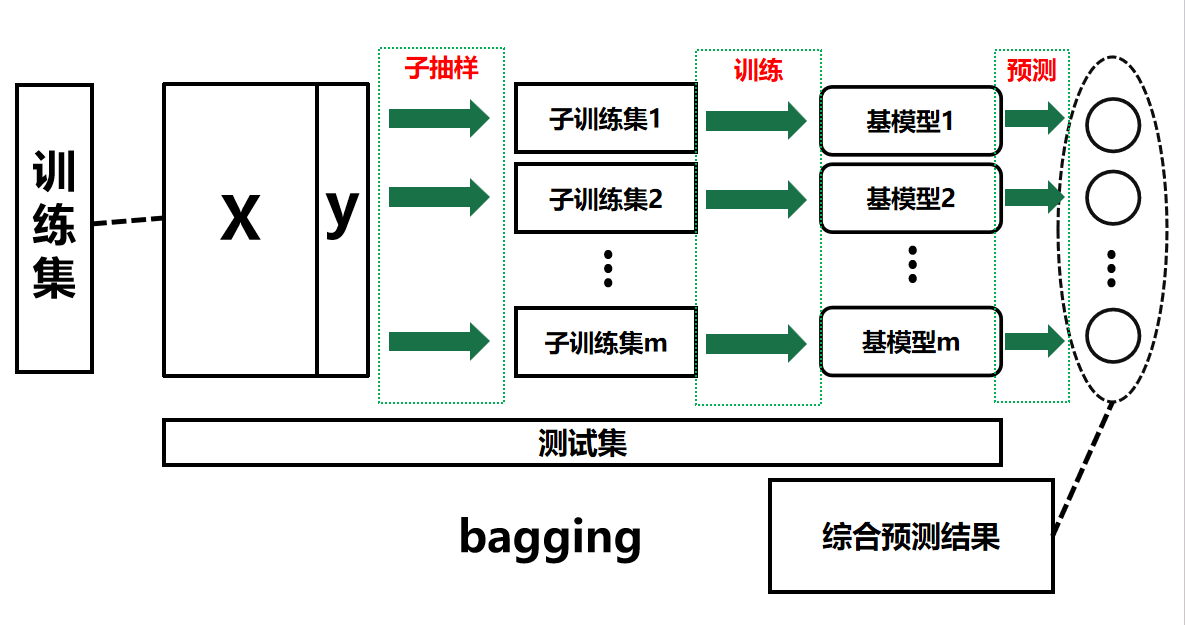
所以，根據以上的例子，我們放到我們的訓練集中去體現這個思想，

那就可以參照下圖進行理解。
在這里插入圖片描述

2 Boosting（提升法）

2.1 算法過程

樣本權重：為訓練集樣本建立權值 $w_i$ ，權值表示對樣本的關注度，對于誤分類概率高的樣本會加大其權值。這樣可以讓模型更關注難以分類的樣本，提升模型性能。

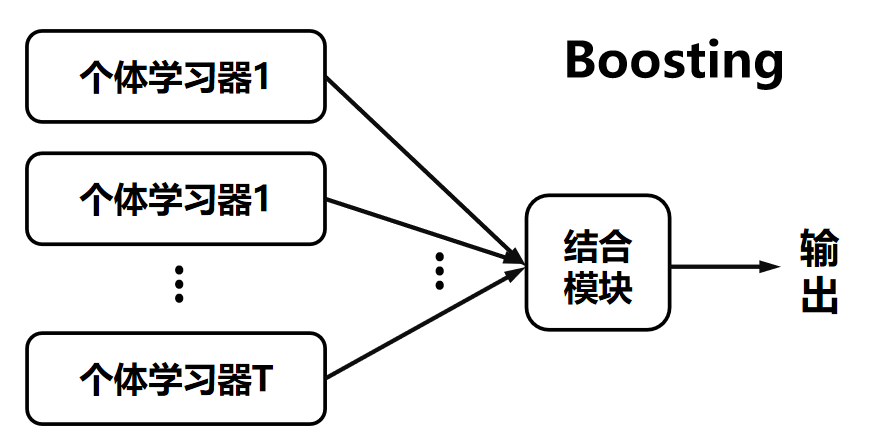
模型組合：迭代生成弱分類器，然后通過一定策略進行組合，例如AdaBoost算法會給弱分類器進行加權線性組合，其中誤差小的弱分類器權值更大。通過這種方式，能讓性能好的弱分類器在最終結果中發揮更大作用。

可以參考下面圖片輔助理解。
在這里插入圖片描述

3 Bagging與Boosting的主要區別

對比項	Bagging	Boosting
樣本選擇	Bootstrap隨機有放回抽樣	訓練集不變，改變樣本權重
樣本權重	均勻取樣，權重相等	依錯誤率調整，錯誤率高的樣本權重越大
預測函數權重	所有預測函數權重相等	誤差小的預測函數權重越大
并行計算	預測函數可并行生成	需按順序迭代生成

4 隨機森林

4.1 基本概念

隨機森林由Bagging + 決策樹組成，其產生是為了解決決策樹泛化能力弱的問題。
通過利用Bagging方法產生不同的數據集來生成多棵決策樹，從而提升預測準確率，但會損失部分直觀解釋性。

4.2 `隨機`含義

樣本隨機：使用Bootstrap方法從樣本集中隨機選取n個樣本用于訓練每棵樹。這樣能保證每棵樹的訓練樣本具有差異性。
特征隨機：從所有屬性中隨機選取k個，然后選擇最佳分割屬性來構建CART決策樹（也可使用SVM等其他模型）。通過特征的隨機選擇，進一步增加了樹的多樣性。

4.3 算法步驟

重復樣本隨機、特征隨機的步驟m次，構建m棵CART決策樹。
多棵樹通過投票表決（如一票否決、少數服從多數、加權多數等方式）來決定分類結果。

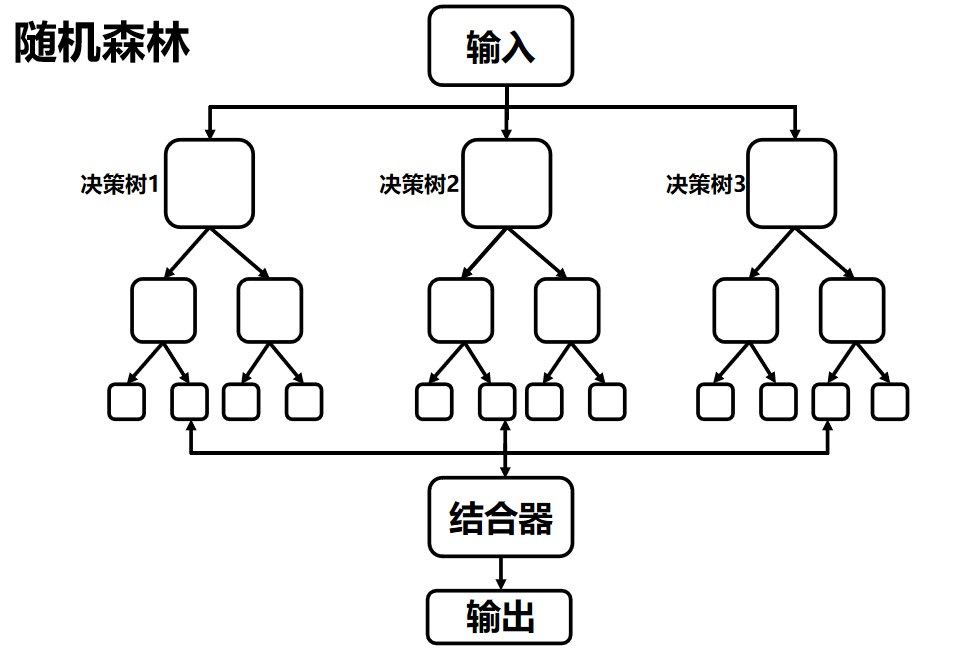
具體流程可以參考下圖：

在這里插入圖片描述

4.4 優點

由于只選擇部分樣本和特征進行訓練，能夠避免模型過擬合。
隨機選擇樣本與特征的方式，使得模型的抗噪能力好、性能穩定。
可以處理高維數據，無需進行特征選擇。
適合進行并行計算，且實現簡單。

4.5 流程可視化與局限性

4.5.1 流程可視化理解

可見下圖，隨機森林先預設超參數（如樹的數量、層數），再通過隨機采樣（樣本 + 特征雙隨機）訓練多棵決策樹，最后整合結果（分類求眾數、回歸求均值）。
流程清晰體現多棵樹并行訓練→結合器統一輸出的模式。

4.5.2 局限性

模型存在泛化與復雜度矛盾：雖通過隨機化提升泛化，但整體過于General，遇到極復雜、超出訓練規律的樣本，因單棵樹能力有限，集成后也難精準處理，即 起點高（基于 Bagging 和決策樹已有基礎）但天花板低（依賴基礎組件能力，難突破單個弱學習器上限） 。
在實際應用中，需結合場景權衡。
簡單規律任務表現好，超復雜、需深度挖掘的場景，可能需更復雜模型配合。

4.6 sklearn函數及參數

4.6.1 關鍵參數`max_features`

Auto/None：使用所有特征。
sqrt：每棵子樹使用總特征數的平方根個特征。
log2： $max\_features = log2(n\_features)$ 。
0.2：子樹使用20%的特征，也可采用0.x格式來考察不同特征占比的作用。
增加max_features理論上可能因為節點選擇更多樣而提升模型性能，這是隨機森林的優勢之一，但會降低單樹的多樣性，并且會使算法速度下降，因此需要平衡選擇。

4.6.2 核心參數解析

`n_estimators`

含義：子樹的數量。
影響：數量越多，模型性能通常更好，但代碼運行速度會變慢。需要選擇處理器能夠承受的高值，默認值為10，一般至少設置為100，以讓預測更優更穩定。

`max_depth`

設置樹的最大深度，默認值為None，此時葉節點要么是單一類別，要么達到min_samples_split條件。

`min_samples_split`

分割內部節點所需的最少樣本數量，默認值為2。

`min_samples_leaf`

葉子節點包含的最少樣本數，默認值為1。

`bootstrap`

控制是否進行有放回抽樣，默認值為True。

`min_impurity_decrease`

規則：只有當分裂后雜質度的減少效果高于該值（默認值為0）時，節點才會分裂。

`min_weight_fraction_leaf`

條件：節點對應的實例數與總樣本數的比值≥該值（默認值為0）時，才能成為葉子節點。

`max_leaf_nodes`

默認值為None，此時會以最優優先方式生成樹，優先選擇雜質少（純度高）的葉子節點。

`min_impurity_split`

閾值：當節點的雜質度高于此值時則進行分裂，低于此值則成為葉子節點，用于控制樹的增長。

`criterion`

"gini"（默認值，用于計算基尼不純度）或"entropy"（用于計算信息增益），用于選擇最優節點。

`splitter`

"best"（默認值，選擇不純度最大的屬性）或"random"（隨機選擇屬性），建議使用默認值。

`n_jobs`

指定引擎可用的處理器數量，-1表示無限制，1表示使用1個，輸入數字n則使用n個，這對于并行的Bagging等集成算法很重要。

`random_state`

使結果可復現，當確定該值后，在參數和訓練數據不變的情況下，結果相同。

4.6 程序示例

from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score# 加載數據集
data = load_iris()
X = data.data
y = data.target# 劃分訓練集和測試集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)# 創建隨機森林分類器
rf = RandomForestClassifier(n_estimators=100, max_features='sqrt', random_state=42)# 訓練模型
rf.fit(X_train, y_train)# 預測
y_pred = rf.predict(X_test)# 計算準確率
accuracy = accuracy_score(y_test, y_pred)
print(f"模型準確率：{accuracy}")