1 引入

1.1?普通二叉樹不適合用數組存儲的原因

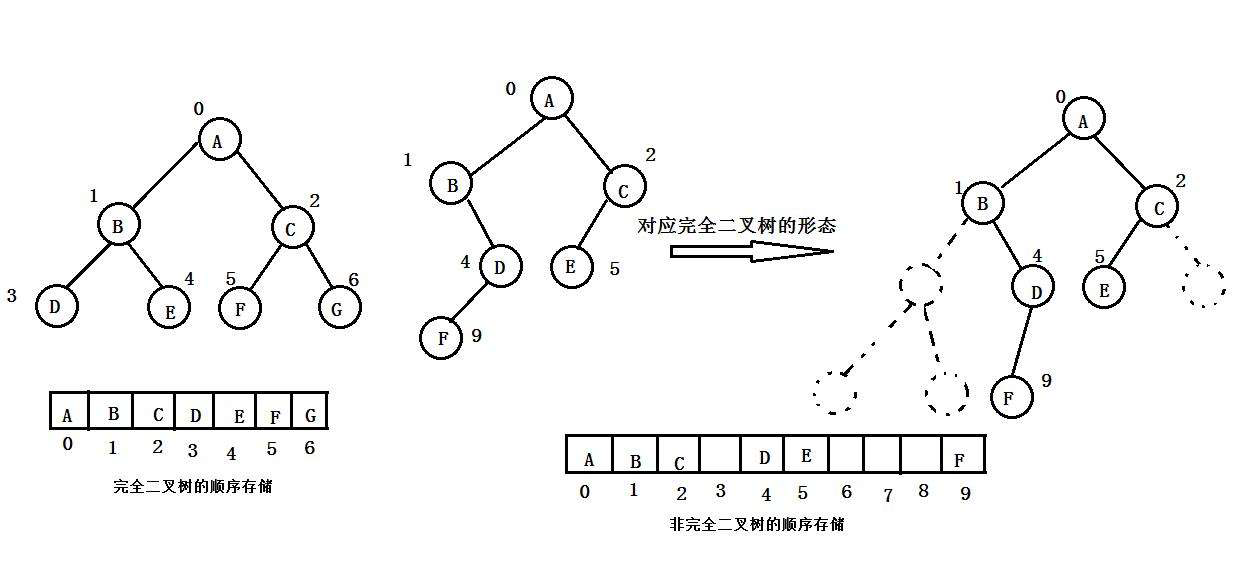
普通二叉樹的結構是 “不規則” 的 —— 節點的左右孩子可能缺失，且缺失位置無規律。
若用數組存儲（按 “層次遍歷順序” 分配索引，即根節點放索引 0，根的左孩子放 1、右孩子放 2，以此類推），缺失的節點會導致數組中出現大量空位置，造成空間浪費。

例如：一棵只有 “右孩子” 的二叉樹（根→右→右→...），按數組存儲時，所有左孩子的位置（索引 1、3、7...）都會空著，這些空位置就是無效浪費。

1.2?完全二叉樹適合順序存儲的原因

完全二叉樹的結構是 “緊湊” 的：

• 除最后一層外，其他層的節點均 “滿”（即每個節點都有左右孩子）；
• 最后一層的節點從左到右 “連續排列”，沒有中間缺失。

這種結構使得按層次遍歷順序存儲時，數組的索引與節點位置完全對應，幾乎沒有空位置。例如：一個高度為 3 的完全二叉樹（共 7 個節點），數組索引 0-6 會被完全填滿，無任何浪費。

1.3?堆用數組存儲的合理性

堆是一種 “特殊的完全二叉樹”（滿足 “大頂堆” 或 “小頂堆” 特性：大頂堆中每個父節點的值≥子節點，小頂堆則≤）。

由于堆本質是完全二叉樹，自然繼承了 “緊湊結構” 的特點，因此適合用數組存儲。

數組存儲堆時，通過索引可快速定位節點的父 / 子節點，規則為（假設節點在數組中索引為i）：

• 左孩子索引：2i + 1；
• 右孩子索引：2i + 2；
• 父節點索引：(i - 1) // 2（整數除法）。

這種對應關系讓堆的核心操作（如 “堆化”“插入”“刪除”）能通過數組索引高效實現，無需額外存儲指針，既省空間又提效。

1.4. “數據結構的堆” 與 “操作系統的堆” 的區分

兩者僅名稱相同，本質完全無關：

• 數據結構的堆：是一種特殊的完全二叉樹，用于實現優先隊列（如任務調度中的 “最高優先級先執行”），核心特性是 “父節點與子節點的大小關系固定”（大頂 / 小頂）。
• 操作系統的堆：是內存中的一塊區域（與 “棧” 相對），用于 “動態內存分配”（如 C 語言malloc、Javanew申請的內存均來自這里），由操作系統的內存管理模塊負責分配與回收。

所以，綜上所述：

堆是一種特殊的完全二叉樹（滿足大頂堆或小頂堆特性），而它的實現依賴于 “順序存儲”（數組）—— 這與二叉樹的存儲特性直接相關。

普通二叉樹因結構不規則，用數組存儲會產生大量空位置（例如僅右孩子存在時，左孩子的索引全為空），空間效率極低；但完全二叉樹不同，其節點按層次緊湊排列，無無規律缺失，用數組存儲時索引可與節點位置一一對應，幾乎無空間浪費。

堆作為完全二叉樹的 “特例”，天然適配數組存儲：我們將堆的節點按層次遍歷順序存入數組，通過索引規則（左孩子2i+1、右孩子2i+2、父節點(i-1)//2）可快速定位任意節點的父子關系。這種存儲方式讓堆的核心操作能通過數組索引直接計算，無需指針，既簡化實現又提升效率（時間復雜度為 O (log n)）。

需特別注意：此處的 “堆” 是數據結構概念，與操作系統中 “管理動態內存的堆區域” 完全無關 —— 前者是一種二叉樹，后者是內存分段，僅名稱巧合。

2 堆的概念

堆是一種特殊的完全二叉樹，分為：

• 大根堆：每個節點的值≥其左右孩子的值，根最大。
• 小根堆：每個節點的值≤其左右孩子的值，根最小。

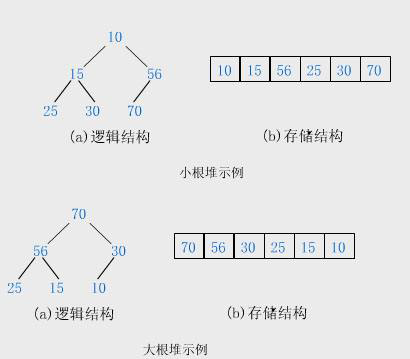
小堆不一定是升序，大堆不一定是降序，所以，成為堆并不代表有序。?

3 堆的經典選擇題辨析

堆作為一種特殊的完全二叉樹，其結構特性（大頂堆 / 小頂堆）和存儲方式（數組順序存儲）決定了它在算法中的高頻應用。本文通過 4 道經典題目，從堆的判斷、刪除重建、初始堆構建到調整過程，帶你深入理解堆的核心邏輯。

3.1 判斷下列關鍵字序列是否為堆

題目：下列關鍵字序列為堆的是（）
A 100,60,70,50,32,65
B 60,70,65,50,32,100
C 65,100,70,32,50,60
D 70,65,100,32,50,60
E 32,50,100,70,65,60
F 50,100,70,65,60,32

解析：堆的核心判斷標準

堆分為大頂堆（每個父節點的值≥子節點）和小頂堆（每個父節點的值≤子節點），判斷序列是否為堆，需驗證所有父節點與子節點的關系是否滿足其一。

數組存儲堆時，節點索引關系為（設節點索引為i）：

• 左孩子：2i+1，右孩子：2i+2

選項 A 分析：100,60,70,50,32,65

• 根節點（i=0）：100，左孩子（i=1）=60，右孩子（i=2）=70 → 100≥60 且 100≥70（滿足大頂堆父節點要求）；
• 節點 i=1（60）：左孩子（i=3）=50，右孩子（i=4）=32 → 60≥50 且 60≥32；
• 節點 i=2（70）：左孩子（i=5）=65 → 70≥65；
  所有父節點均滿足 “≥子節點”，是大頂堆。

其他選項均不滿足：

• 選項 B：根節點 60 的右孩子 100＞60，不滿足大頂堆；
• 選項 C：節點 i=1（100）的右孩子（i=4）=50，左孩子（i=3）=32，但根節點 65＜100，不滿足大頂堆；
• 其余選項同理可證不滿足堆的定義。

答案：A

3.2 小根堆刪除堆頂后重建的比較次數

題目：已知小根堆為 8,15,10,21,34,16,12，刪除關鍵字 8 之后需重建堆，比較次數是（）。
A 1 B 2 C 3 D 4

解析：小根堆的刪除與重建流程

小根堆刪除堆頂（最小值）的步驟：

1. 替換堆頂：用最后一個元素替換堆頂（保證結構緊湊）；
2. 向下調整：從新堆頂開始，與左右孩子中較小的節點比較，若不滿足 “父≤子” 則交換，重復至平衡。

具體步驟：

原堆（數組）：[8,15,10,21,34,16,12]（長度 7，索引 0-6）

• 刪除堆頂 8 后，用最后一個元素 12 替換堆頂，新數組為[12,15,10,21,34,16]（長度 6，索引 0-5）；
• 向下調整 12（堆頂）：
  • 左孩子（i=1）=15，右孩子（i=2）=10 → 較小的孩子是 10（i=2）；
  • 比較 12 與 10：12＞10，交換 → 數組變為[10,15,12,21,34,16]；
  • 調整 12（現在在 i=2）：左孩子（i=5）=16，右孩子無；
  • 比較 12 與 16：12＜16，無需交換，調整結束。

比較次數統計：

• 第一次：12 與左孩子 15、右孩子 10 比較（2 次）；
• 第二次：12 與左孩子 16 比較（1 次）；
  共 3 次比較。

答案：C

3.3 堆排序的初始堆構建

題目：一組記錄排序碼為 (5,11,7,2,3,17)，利用堆排序方法建立的初始堆為（）
A(11,5,7,2,3,17) B(11,5,7,2,17,3) C(17,11,7,2,3,5) D(17,11,7,5,3,2) E(17,7,11,3,5,2) F(17,7,11,3,2,5)

解析：堆排序的初始堆（大頂堆）構建

堆排序的第一步是構建大頂堆（根節點為最大值），步驟：

1. 從最后一個非葉子節點開始（索引(n-1)//2），依次向前調整；
2. 調整規則：若父節點＜子節點中較大值，則交換，并遞歸調整交換后的子節點。

具體步驟：

排序碼：[5,11,7,2,3,17]（長度 6，索引 0-5）

• 最后一個非葉子節點索引：(6-1)//2=2（值為 7）；
  • 節點 i=2（7）的右孩子 i=5（17）→ 7＜17，交換 → 數組變為[5,11,17,2,3,7]；
• 前一個非葉子節點 i=1（11）：左孩子 i=3（2），右孩子 i=4（3）→ 11≥兩者，無需調整；
• 第一個非葉子節點 i=0（5）：左孩子 i=1（11），右孩子 i=2（17）→ 5＜17，交換 → 數組變為[17,11,5,2,3,7]；
• 調整交換后 i=2（5）：右孩子 i=5（7）→ 5＜7，交換 → 數組變為[17,11,7,2,3,5]，此時所有父節點均滿足大頂堆規則。

答案：C

3.4 最小堆刪除堆頂后的結果

題目：最小堆 [0,3,2,5,7,4,6,8]，在刪除堆頂元素 0 之后，其結果是（）
A[3，2，5，7，4，6，8] B[2，3，5，7，4，6，8] C[2，3，4，5，7，8，6] D[2，3，4，5，6，7，8]

解析：最小堆的刪除與調整

最小堆刪除堆頂（最小值）的流程與題目 2 一致：替換堆頂→向下調整（保證父≤子）。

具體步驟：

原堆：[0,3,2,5,7,4,6,8]（長度 8，索引 0-7）

• 刪除 0 后，用最后一個元素 8 替換堆頂 → 新數組[8,3,2,5,7,4,6]（長度 7，索引 0-6）；
• 向下調整 8（堆頂）：
  • 左孩子 i=1（3），右孩子 i=2（2）→ 較小孩子是 2（i=2）；
  • 8＞2，交換 → 數組變為[2,3,8,5,7,4,6]；
• 調整 8（i=2）：
  • 左孩子 i=5（4），右孩子 i=6（6）→ 較小孩子是 4（i=5）；
  • 8＞4，交換 → 數組變為[2,3,4,5,7,8,6]；
• 8（i=5）無孩子，調整結束。

答案：C

?