圖論：Dijkstra算法

昨天介紹了最小生成樹的兩個算法，最小生成樹的兩個算法旨在求解無向有權圖中的最小代價聯通圖的問題，那么對于有向有權圖，從起點到終點的最小花費代價問題就可以用 Dijkstra 算法來解決而且Dijkstra算法可以求出來從起始點開始到所有節點的最短距離！他和最小生成樹的prim算法十分類似，也是三部曲，最短路是圖論中的經典問題即：給出一個有向圖，一個起點，一個終點，問起點到終點的最短路徑。

樸素版Dijkstra算法

dijkstra算法：在有權圖（權值非負數）中求從起點到其他節點的最短路徑算法。

dijkstra 算法可以同時求起點到所有節點的最短路徑
權值不能為負數

dijkstra三部曲：

第一步，選源點到哪個節點近且該節點未被訪問過
第二步，該最近節點被標記訪問過
第三步，更新非訪問節點到源點的距離（即更新ans數組）

ans數組用來記錄每一個節點距離起始點的最小距離。

循環n次，每一次都能確定一個最優點（其實和prim算法一樣都是用了貪心的策略，因為之后的所有的點的選取都是基于目前所有的可達路徑，所以要在當前所有的可達路徑中選一個權值最小的路徑，以其為基準再繼續更新之后的可達點，當一個點被更新到最短路中的時候【即被標記訪已訪問的時候】，就說明在他之前所有可以到達他的路徑都遍歷過了，因為他是被所有的前面的可達他的點都遍歷過的）。

說多了容易迷糊，來看一個模版題來促進對算法以及代碼模板的理解

參加科學大會

題目鏈接：參加科學大會

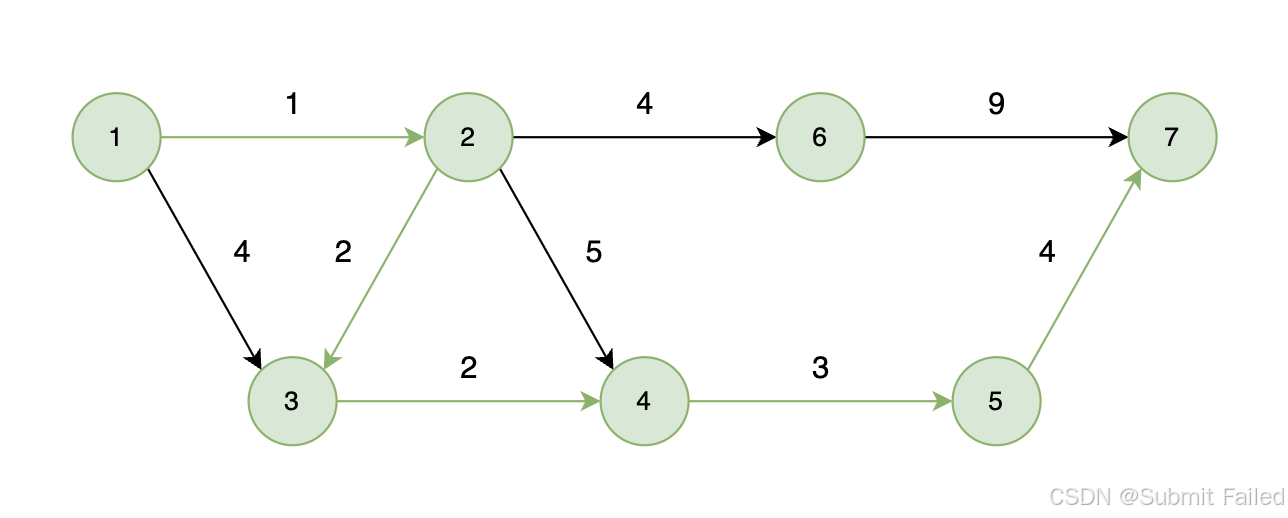
這道題還是相對簡單一點的，因為已經固定了起點是1，終點是n，所以不需要對起點和終點進行分析，直接套用模板即可。注意建圖的時候如果用鄰接矩陣時開[n][n]二維數組m只是邊數！

#include <bits/stdc++.h>
using namespace std;
#define int long long 
#define endl '\n'
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define pii pair<int,int>
#define fi first
#define se second
const int inf = 0x3f3f3f3f3f3f3f3f;
int n,m;void solve()
{cin>>n>>m;vector<vector<int>> e(n+1,vector<int>(n+1,inf));//建圖vector<bool> v(n+1,false);//標記數組vector<int> ans(n+1,inf);//所有的點到起點的最短距離（最小代價）for(int i=1;i<=m;i++){int u,v,w;cin>>u>>v>>w;e[u][v] = w;//建圖}ans[1] = 0;//Dijkstra算法三部曲for(int i=1;i<=n;i++){int mi = inf;int index = 0;//遍歷找不在未訪問的距離起點最近的點for(int j=1;j<=n;j++)//因為之后的所有答案都會在現在的路徑基礎上累加 所以在現有路徑中挑最短的{if(!v[j] && ans[j] < mi){mi = ans[j];index = j;}}//將最近點標記為已訪問v[index] = true;//更新所有未訪問的可達點到起點的最短距離for(int j=1;j<=n;j++){if(!v[j] && e[index][j] + ans[index] < ans[j]) ans[j] = ans[index] + e[index][j];}}if(ans[n] == inf) cout<<"-1"<<endl;else cout<<ans[n]<<endl;
}signed main()// Don't forget pre_handle!
{IOSint T=1;
//	cin>>T;while(T--) solve(); return 0;
}

這里奉上Dijkstra樸素版的模板，ICPCer可拿~【適用于n<=1e3且沒有負邊權（用SPFA）】?

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define pii pair<int,int>
#define fi first
#define se second
const int inf = 0x3f3f3f3f3f3f3f3f;  // 定義無窮大void solve()
{// 輸入點數和邊數int n,m;cin>>n>>m;// 鄰接矩陣存圖，初始化為infvector<vector<int>> e(n+1,vector<int>(n+1,inf));// 標記數組，記錄是否已確定最短路vector<bool> v(n+1,false);// 存儲起點到各點的最短距離vector<int> ans(n+1,inf);// 建圖，處理邊輸入for(int i=1;i<=m;i++){int u,v,w;cin>>u>>v>>w;e[u][v]=w;  // 有向圖建邊// e[v][u]=w; // 如果是無向圖需要加上這行}// 初始化，起點距離設為0ans[1]=0;//起點和終點看題目要求// Dijkstra主過程，循環n次for(int i=1;i<=n;i++){int mi=inf;     // 當前未處理節點中的最小距離int index=0;    // 對應的節點編號// 遍歷所有節點，找出未處理且距離最小的節點for(int j=1;j<=n;j++){if(!v[j]&&ans[j]<mi){mi=ans[j];index=j;}}// 標記該節點已處理v[index]=true;// 松弛操作：通過該節點更新其他節點的距離for(int j=1;j<=n;j++){if(!v[j]&&e[index][j]+ans[index]<ans[j]){ans[j]=ans[index]+e[index][j];}}}// 輸出結果，如果不可達輸出-1if(ans[n]==inf) cout<<"-1"<<endl;else cout<<ans[n]<<endl;
}
signed main()
{IOS;int T=1;//cin>>T;while(T--){solve();}return 0;
}

堆優化版Dijkstra

題目重現

堆優化就是利用小頂堆來避免每次都遍歷尋找最值，并且用鄰接表代替鄰接矩陣更能優化第二個for循環，因為鄰接表中存的就是這個點之后所連接的點，直接用auto遍歷即可，不過需要分清里面的fi和se分別都對應的哪些變量！

參加科學大會：堆優化版代碼：

#include <bits/stdc++.h>
using namespace std;
#define int long long 
#define endl '\n'
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define pii pair<int,int>
#define fi first
#define se second
const int inf = 0x3f3f3f3f;
const int N = 520;
vector<vector<pii>> e(N);//鄰接表
vector<int> ans(N,inf);//各個點到起點的最近距離
vector<bool> f(N,false);//標記訪問數組
priority_queue<pii,vector<pii>,greater<pii>> q;//最小堆優化
int n,m;void solve()
{cin>>n>>m;for(int i=1;i<=m;i++){int u,v,w;cin>>u>>v>>w;e[u].push_back({v,w});//用鄰接表建圖}ans[1] = 0;q.push({ans[1],1});//fi為ans se為索引while(!q.empty()){int mi = q.top().fi;int index = q.top().se;q.pop();if(f[index]) continue;//如果訪問過就continue！！！！！f[index] = true;for(auto i : e[index]){//i.fi是點的索引 i.se是邊權if(ans[index] + i.se < ans[i.fi]){ans[i.fi] = ans[index] + i.se;q.push({ans[i.fi],i.fi});//別忘記在找到一個點之后就更新ans[i.fi]//在找到更優解的時候再加入隊列!!!}}}if(ans[n] == inf) cout<<"-1"<<endl;else cout<<ans[n]<<endl;
}signed main()// Don't forget pre_handle!
{IOSint T=1;
//	cin>>T;while(T--) solve(); return 0;
}

這里同樣奉上堆優化版的模板，ICPCer可拿~

#include <bits/stdc++.h>
using namespace std;
#define int long long 
#define endl '\n'
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define pii pair<int,int>
#define fi first
#define se second
const int inf = 0x3f3f3f3f;
const int N = 520;// Dijkstra堆優化模板（鄰接表實現）
// 適用情況：稀疏圖，點數較多（mlogn復雜度）
// 功能：求單源最短路，解決非負權圖
// 注意：inf需要根據題目調整，避免溢出vector<vector<pii>> e(N);  // 鄰接表存圖
vector<int> ans(N, inf);   // 存儲起點到各點的最短距離
vector<bool> f(N, false);  // 標記是否已確定最短路
priority_queue<pii, vector<pii>, greater<pii>> q;  // 小根堆優化
int n, m;void solve()
{cin >> n >> m;// 鄰接表建圖for(int i = 1; i <= m; i++){int u, v, w;cin >> u >> v >> w;e[u].push_back({v, w});  // 有向圖建邊// e[v].push_back({u, w}); // 無向圖需要加上這行}// 初始化起點距離ans[1] = 0;q.push({ans[1], 1});  // first存距離，second存節點編號// Dijkstra主過程while(!q.empty()){int mi = q.top().fi;    // 當前最小距離int index = q.top().se; // 對應節點q.pop();// 如果該節點已確定最短距離，跳過if(f[index]) continue;f[index] = true;  // 標記已確定// 遍歷所有鄰接點for(auto i : e[index]){// i.fi是鄰接點索引，i.se是邊權if(ans[index] + i.se < ans[i.fi]){ans[i.fi] = ans[index] + i.se;  // 松弛操作q.push({ans[i.fi], i.fi});      // 將新距離加入堆}}}// 輸出結果if(ans[n] == inf) cout << "-1" << endl;else cout << ans[n] << endl;
}signed main()
{IOS;int T = 1;//cin >> T;while(T--){solve();}return 0;
}

一定一定要注意訪問過就continue!每次的操作（步驟1和3都是對未訪問元素的操作!）

接下來就運用一下Dijkstra算法吧！

代價轉移

題目鏈接：代價轉移

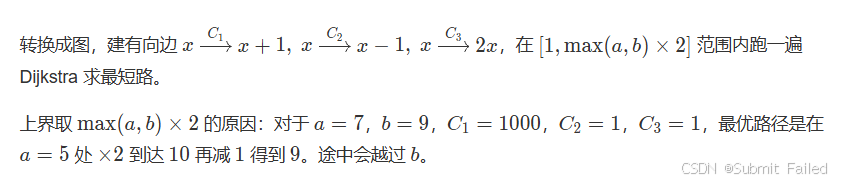
這道題與眾不同的就是沒有直接給出圖的構造，而是需要不斷的動態的更新，不過換湯不換藥，不過要注意對于動態生成的節點要判斷是否合理，如果不合理的話就應該continue防止導致未定義越界（負節點或超大節點）導致死循環！max(a,b) * 2僅僅是合理的范圍，不是動態生成的點的范圍

下面來看詳細代碼：

// Problem: 代價轉移
// Contest: NowCoder
// URL: https://ac.nowcoder.com/acm/contest/113664/B
// Memory Limit: 512 MB
// Time Limit: 2000 ms
// 
// Powered by CP Editor (https://cpeditor.org)#include <bits/stdc++.h>
using namespace std;
#define int long long 
#define endl '\n'
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define pii pair<int,int>
#define fi first
#define se second
const int inf = 0x3f3f3f3f3f3f3f3f;void solve()
{int a,b,c1,c2,c3;cin>>a>>b>>c1>>c2>>c3;if(a >= b)//對特殊情況進行判斷{cout<<(a - b) * c2 <<endl;return ;}//Dijkstra求最短路:int N = max(a,b) * 2;//先預定一個可達點范圍vector<int> ans(N+1,inf);//初始化為最大vector<bool> v(N+1,false);//標記訪問數組priority_queue<pii,vector<pii>,greater<pii>> q;//小頂堆ans[a] = 0;//依舊初始化q.push({0,a});//首先將起點入隊while(!q.empty()){int value = q.top().fi;//直接找出最小值int index = q.top().se;//q.fi是代價 q.se數q.pop();//將這個點放入最短路徑中了（不在非訪問的數里面了）if(v[index]) continue;//一定一定別忘記 Dijkstra的核心v[index] = true;//標記已訪問pii adj[] = {{index + 1,c1},{index - 1,c2},{index * 2,c3}};//動態生成三個新節點for(auto i : adj)//對三個節點進行遍歷{if(i.fi < 1 || i.fi > N) continue;//注意要對新節點的合理性檢查 常規圖中都是合理點 但是這里是不斷動態生成的點 需要檢查if(ans[index] + i.se < ans[i.fi])//更新更優解{ans[i.fi] = ans[index] + i.se;q.push({ans[i.fi],i.fi});//在找到滿足條件的值之后再入隊}}}cout<<ans[b]<<endl;
}signed main()// Don't forget pre_handle!
{IOSint T=1;cin>>T;while(T--) solve(); return 0;
}

以上內容就是關于Dijkstra算法的兩種實現思路了，感興趣的小伙伴可以收藏起來到整理模版的時候直接食用！